ГДЗ Тарасенкова Математика 6 клас завдання 989 - 1055 § 21 Модуль числа Відповіді до підручника
3авдання 989
Відстань від D(–5) до початку відліку 5; |–5| = 5
Відстань від C(–2) до початку відліку 2; |–2| = 2
Відстань від A(2) до початку відліку 2; |2| = 2
Відстань від B(5) до початку відліку 5; |5| = 5
Відстань від F(7) до початку відліку 7; |7| = 7

 

3авдання 990
1) Так
2) Ні
3) Так
4) Так
5) Ні
6) Ні
7) Так
8) Ні
Завдання 991
1) Так
2) Ні
3) Ні
4) Так
5) Ні
Завдання 992
1) Ні
2) Ні
3) Так
Завдання 993
1) Відстань від А(3,5) до початку відліку 3,5; |3,5| = 3,5
2) Відстань від В(–7) до початку відліку 7; |–7| = 7
3) Відстань від С(3) до початку відліку 3; |3| = 3
4) Відстань від D(–6) до початку відліку 6; |–6| = 6

 

3авдання 994
1) Відстань від А(0) до початку відліку 0; |0| = 0
2) Відстань від В(–5) до початку відліку 5; |–5| = 5
3) Відстань від С(8) до початку відліку 8; |8| = 8

 

3авдання 995
1) |х| = 5, х = –5 або  х = 5
2) |х| = 4,5, х = –4,5 або х = 4,5
3) |х| = 2,5, х = –2,5 або х = 2,5
4) |х| = 1, х = –1 або х =1
Завдання 996
1) |х| = 4, х = –4 або х = 4
2) |х| = 3,5, х = –3,5 або х = 3,5
3) |х| = 3, х = –3 або х = 3
4) |х| = 1,5, х = –1,5 або х = 1,5
Завдання 997
1) |х| = 2, тому х = –2 і  х = 2; Кооринати точок (-2) і (2)
2) |х| = 4, тому х =–4 і х = 4; Кооринати точок (-4) і (4)
3) |х| = 3, тому х = –3 і х = 3. Кооринати точок (-3) і (3)

 

3авдання 998
1) |х| = 2, тому х = –2 і х = 2; Кооринати точок (-2) і (2)
2) |х| = 2, тому х = –8 і х = 8. Кооринати точок (-8) і (8)

 

3авдання 999
1) |х| = 1, тому до початку відліку 1 од. відрізок.
2) |х| = 12, тому до початку відліку 12 од. відрізків.
3) |х| = 4/9, тому до початку відліку 4/9 од. відрізки.
4) |х| = 3,8, тому до початку відліку 3,8 од. відрізки.

 

3авдання 1000
1) |b| = 5,2, тому до початку відліку 5,2 од. відрізків.

 

3авдання 1001
1) |–41| = 41 і |41| = 41, а 41 = 41, тому |–41| = |41|
2) |–2,5| = 2,5 і |2,5| = 41, а 2,5 = 2,5, тому |–2,5| = |2,5|
3) |0,2| = 0,1 = 1/5 і |–1/5| =1/5, а 1/5 = 1/5, тому |0,2| = |–1/5|
4) |–1,5| = 1,5 і |1,5| = 1,5, а 1,5 = 1,5, тому |–1,5| = |1,5|

 

3авдання 1002
|–2,8| = 2,8 і |2,8| = 2,8, а 2,8 = 2,8, тому |2,8| = |–2,8|

 

3авдання 1003
Скориставшись координатною прямою, обґрунтуйте, що: |a| = |–a|.
|а| = а і |–а| = а, оскільки а = а, тому |–а| = |а|

 

3авдання 1004

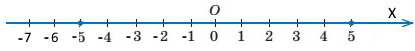
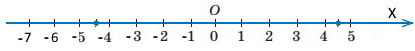
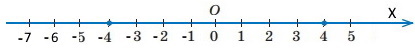
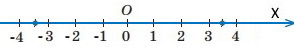
1) |–3| • |–4| = 3 • 4 = 12

2) |28| : |7| = 28 : 7 = 4

3) |0| • |–5| = 0 • 5 = 0

4) |–1/2| + |2| = 1/2 + 2 = 2 1/2

5) |–8/9| • |–9| = 8/9 • 9 = 8

6) |144| : |–12| = 144 : 12 = 12
Завдання 1005 Протилежні числа

1) 0,6 = 3/5,  і –3/5 Так

2) –1,4 = –12/5 = –7/5 і 7/5 Так

3) 1,5 і 3/2 Ні, бо числа одного знаку

4) –2,2 і –11/5 Ні, бо числа одного знаку
Завдання 1006 Протилежні числа

1) 5/2 і 2/5 Ні, бо числа одного знаку

2) 2/5 і –5/2 Ні, бо значення модулів чисел різне 

3) 2/5 і –2/5 Так

 

3авдання 1007

Пари протилежних чисел: 32 і –32; 0,4 і –0,4; 4/5 і –4/5

 

3авдання 1008
Число
13
–6
30
5,7
0
–8,7
–2 13/14
–0,8
2,6
Протилежне число
–13
6
–30
–5,7
0
8,7
2 13/14
 0,8
–2,6
Завдання 1009, 1010 Протилежне число

1) 5,6; –5,6

2) 38; –38

3) 0; 0

4) –5. 5

1) 41; –41

2) –7,2; 7,2

3) 213; –213

4) –8,09. 8,09
Завдання 1011, 1012

1) Якщо –р = 9, тоді р = –9

2) Якщо –р = –20, тоді р = 20

3) Якщо –р = 0,4, тоді р = –0,4

4) Якщо –р = 0, тоді р = 0

1) якщо х = 9,5, тоді –х = –(9,5) = –9,5

2) якщо х = –6, тоді –х = –(–6) = 6
Завдання 1013 Рівняння

1) –х = 34

   х = –34

2) –х = 5

   х = –5

3) –х = –65

   х = 65

4) –х = –86

   х = 86

5) –х = –(–8)

   х = –8

6) –х = –(–5)

   х = –5
Завдання 1014

1) –х = 28

   х = –28

2) –х = 2

   х = –2
Завдання 1015

Число

13

−2 13/14

6

 –8,7 –0,8 0,8 –4 8/9 4 8/9

Протилежне число

–13

2 13/14

–6

8,7

0,8

 –0,8 4 8/9 –4 8/9

Модуль числа

13

2 13/14

6

8,7

0,8

0,8

4 8/9

4 8/9
Модуль протилежного числа 13 2 13/14 6 0,8

–28

 0,8

4 8/9

 4 8/9
Завдання 1016

1) |7| = 7

2) |–8| = 8

3) |–42| = 42

4) |0| = 0

5) |–1| = 1

6) |6/7| = 6/7

7) |100| = 100

8) |–250| = 250

9) |–8/17| = 8/17

10) |0,01| = 0,01

11) |2,8| = 2,8

12) |–12/3| = 12/3
Завдання 1017 Знайдіть модуль даного числа і числа, протилежного до нього:

1) |0,3| = 0,3; |–0,3| = 0,3

2) |0| = 0; |–0| = 0

3) |–10| = 10; |10| = 10

4) |–1/2| = 1/2; |1/2| = 1/2
Завдання 1018

1) |х| = 18, х = 18 або х =–18

2) |х| = 5,4, х = 5,4 або х = –5,4

3) |х| = 12,1, х = 12,1 або х = –12,1

4) |х| = 254, х = 254 або х = –254

5) |х| = 2/3, х = 2/3 або х –2/3

6) |х| = 1/17, х = 1/17 або х = –1/17
3авдання 1019

1) –24

2) –0,4

3) –14,25

4) –311
Завдання 1020 Рівняння

1) |х| = 15

    х = 15 або х = –15

3) |х| = 4,5

    х = 4,5 або х = –4,5

5) |х| = 2/3

    х = 2/3 або х = –2/3

2) |х| = 100

    х = 100 або х = –100

4) |х| = 7,2

    х = 7,2 або х = –7,2

6) |х| = 0

    х = 0
Завдання 1021 

1) |х| = 1

    х = 1 або х = –1

3) |х| = 7,8

    х = 7,8 або х = –7,8

2) |х| = 125

    х = 125 або х = –125

3) |х| = 6/7

    х = 6/7 або х = – 6/7
Завдання 1022 

1) а) Якщо х = 0,4, тоді 5 + 8 • |х| = 5 + 8 • |0,4| = 5 + 8 • 0,4 = 5 + 3,2 = 8,2

б) якщо х = –0,4, тоді 5 + 8 • |х|= 5 + 8 • |–0,4| = 5 + 8 • 0,4 = 5 + 3,2 = 8,2

2) а) якщо х = 3/4, тоді 17 – 16 • |х|= 17 – 16 • |3/4| = 17 – 16 • 3/4 = 17 – 12 = 5

б) якщо х = –3/4, тоді 17 – 16 • |х| = 17 – 16 • |– 3/4|= 17 – 16 • 3/4 = 17 – 12 = 5

 

3авдання 1023

1) |15| + |38| = 15 + 38 = 53; протилежне число (–53)

2) |–16| + |11| = 16 + 11 = 27; протилежне число (–27)

3) |43| + |–28| = 43 + 28 = 71; протилежне число (–71)

4) |–101| + |–6| = 101 + 6 = 107; протилежне число (–107)

 

3авдання 1024

1) |14| – |12| = 14 – 12 = 2; протилежне число (–2)

2) |–21| – |21| = 21 – 21 = 0; протилежне число 0

3) |61| – |–31| = 61 – 31 = 30; протилежне число (–30)

4) |–11| – |–11| = 11 – 11 = 0; протилежне число 0

 

3авдання 1025

а

15

7,8

90

 0 –23,4

–a

–15

 –7,8 –90 0 23,4

|a|

15

 7,8 90 0 23,4
|–a| 15 7,8 90 0 23,4
–|a| –15 –7,8 –90 0

–23,4
Завдання 1026

Спираючись на координатну пряму, знайдіть відстань між точками:

1) А(–2) і В(3); АВ = |–2| + |3| = 2 + 3 = 5

2) A(3) і В(–2); АВ = |3| + |–2| = 3 + 2 = 5

3) A(–5) і В(3); АВ = |–5| + |3| = 5 + 3 = 8

4) А(–3) і В(5); АВ = |–3| + |5| = 3 + 5 = 8

5) C(2) і D(7); CD = 7 – 2 = 5

6) C(7) і D(2); CD = 7 – 2 = 5

5) C(5) і D(11); CD = 11 – 5 = 6

6) C(11) і D(5); CD = 11 – 5 = 6

7) M(–8) і N(–4); MN = |–8| – |–4| = 8 – 4 = 4

8) M(–4) і N(–8); MN = |–8| – |–4| = 8 – 4 = 4

9) M(–6) і N(–9); MN = |–9| – |–6| = 9 – 6 = 3

10) M(–9) і N(–6); MN = |–9| – |–6| = 9 – 6 = 3

 

3авдання 1027

1) А(–4) і B(3); АВ = |–4| + |3| = 7

2) C(1) і D(4); CD = |1| + |4| = 5

3) M(–2) і N(–6). MN = |–2| + |–6| = 8

 

3авдання 1028

Знайдіть суму відстаней від даних чисел до початку відліку та відстань між даними числами на координатній прямій:

1) (|0,6| + 0) + (0 + |–3|) = 0,6 + 3 = 3,6; |0,6| + |–3| = 0,6 + 3 = 3,6

2) (|24| + 0) + (0 + |–12|) = 24 + 12 = 36; |24| + |–12| = 24 + 12 = 36

3) (|10| + 0) + (0 + |–5|) = 10 + 5 = 15; |10| + |–5| = 10 + 5 = 15

4) (|–15| + 0) + (0 + |6|) = 15 + 6 = 21; |–15| + |6| = 15 + 6 = 21

5) (|–12| + 0) + (0 + |7|) = 12 + 7 = 19; |–12| + |7| = 12 + 7 = 19

6) (|–6| + 0) + (0 + |15|) = 6 + 15 = 21; |–6] + |15| = 6 + 15 = 21

 

3авдання 1029

1) (|6| + 0) + (0 + |–3|) = 6 + 3 = 9; |6| + |–3| = 6 + 3 = 9

2) (|4| + 0) + (0 + |–8|) = 4 + 8 = 12; |4| + |–8| = 4 + 8 = 12

3) (|–7| + 0) + (0 + |5|) = 7 + 5 = 12; |–7| + |5| = 7 + 5 = 12

 

3авдання 1030

1) (|0,6| + 0) + (0 + |3|) = 0,6 + 3 = 3,6; 3 – 0,6 = 2,4

2) (|24| + 0) + (0 + |12|) = 24 + 12 = 36; 24 – 12 = 12

3) (|10| + 0) + (0 + |5|) = 10 + 5 = 15; 10 – 5 = 5

4) (|15| + 0) + (0 + |6|) = 15 + 6 = 21; 15 – 6 = 9

5) (|12| + 0) + (0 + |7|) = 12 + 7 = 19; 12 – 7 = 5

6) (|6| + 0) + (0 + |15|) = 6 + 15 = 21; 15 – 6 = 9

 

3авдання 1031

Знайдіть суму відстаней від даних чисел до початку відліку та відстань між даними числами на координатній прямій:

1) (|6| + 0) + (0 + |3|) = 6 + 3 = 9; 6 – 3 = 3

2) (|4| + 0) + (0 + |8|) = 4 + 8 = 12; 8 – 4 = 4

3) (|7| + 0) + (0 + |5|) = 7 + 5 = 12; 7 – 5 = 2

 

3авдання 1032

1) (|–0,6| + 0) + (0 + |–3|) = 0,6 + 3 = 3,6; 3 – 0,6 = 2,4

2) (|–24| + 0) + (0 + |–12|) = 24 + 12 = 36; 24 – 12 = 12

3) (|–10| + 0) + (0 + |–5|) = 10 + 5 = 15; 10 – 5 = 5

4) (|–15| + 0) + (0 + |–6|) = 15 + 6 = 21; 15 – 6 = 9

5) (|–12| + 0) + (0 + |–7|) = 12 + 7 = 19; 12 – 7 = 5

6) (|–6| + 0) + (0 + |–15|) = 6 + 15 = 21; 15 – 6 = 9

 

3авдання 1033

1) (|–6| + 0) + (0 + |–3|) = 6 + 3 = 9; 6 – 3 = 3

2) (|–4| + 0) + (0 + |–8|) = 4 + 8 = 12; 8 – 4 = 4

3) (|–7| + 0) + (0 + |–5|) = 7 + 5 = 12; 7 – 5 = 2

 

3авдання  1034, 1035

1) одиничний відрізок 3 : 6 = 0,5

2) одиничний відрізок 2 : 6 = 1/3

1) Одиничний відрізок 4 : 12 = 1/3

2) одиничний відрізок 6 : 12 = 0,5
Завдання 1037

Скориставшись координатною прямою, поясніть суть твердження:

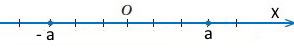
1) число, протилежне до додатного числа, є від’ємним;

Число, протилежне до додатного числа, знаходиться на однаковій відстані ліворуч від початку відліку О, тому є від’ємним. 

2) число, протилежне до від’ємного числа, є додатним.

Число, протилежне до від'ємного числа, знаходиться на однаковій відстані праворуч від початку відліку О, тому є додатним. 

 

3авдання 1037

Знайдіть число, протилежне до числа, яке протилежне до числа:

Число, яке протилежне до числа, яке протилежне до числа а, — це те саме число а.

1) 36

2) 217

3) –96

4) –127
Завдання 1038

Якщо а = –5,002,  тоді |а| + а= |–5,002| + 5,002 = 5,002 + 5,002 = 10,004

 

3авдання 1039

x

13

0

–8,7

23

–0,5

–8

–2,8

–7

y

5

0

0 

–23

–2

3

 –7,4 –23

|x| + |y|

18

0

8,7

46

 2,5 11 10,2 30

Закономірність: |x| + |y| ≥ 0

 

3авдання 1940

1) (|–11|– |–12| : 3) : |(21 : |–7| + |5/2| • 1,6)|= (11 – 12 : 3) : |(21 : 7 + + 5/2 • 8/5)| =

= (11 – 4) : |(3 + 4)| = 7 : 7 = 1; 2) |–25| : |–5| + |–7/3| • 3/2 + |–0,5| =

= 25 : 5 + 7/3 • 3/2 + 0,5 = 5 + 3,5 + 0,5 = 9

 

3авдання 1041

Чи правильно, що:

1) протилежним до числа |–3| є число –3; Так, бо |–3| = 3, а протилежне число –3

2) протилежним до числа 4 є число –|–4|? Так, бо –|–4| = –4, а протилежне число 4

 

3авдання 1042

Чи існує таке число a, що:

1) |a| = –|a|; Так, якщо а = 0, |0| = 0, –|0| = 0

2) |–a| = –|a|? Так, якщо а = 0, бо |–0| = 0 і –|0| = 0

 

3авдання 1043 Рівняння

1) |х| – 70 = 304

    |х| = 100

    х = 100 або х = –100

3) |х| – 32 = 79

    |х| = 111

    х = 111 або х = –111

5) |–х| = –4

    не має розв’язків

2) |х| + 55 = 68

    |х| = 13

    х = 13 або х = –13

4) |–х| = 54,9

    х = 54,9 або х =54,9

6) –|х| = –12

     |х| = 12

     х = 12 або х = –12
Завдання 1044

1) |–х| = 4,2

    х = 4,2 або х = –4,2

3) |–х| = 0

    х = 0

2) |–х| = –115

   не має розв’язків

4) 11 + |х| = 43

   |х| = 32

   х = 32 або х = –32
Завдання 1045

1) 20 % числа |–100|; 

|–100| — 100%

 х — 20%

|–100|/х = 100/20; х = |–100| • 20 : 100 = 100 • 20 : 100 = 20

2) 75 % суми |250| + |1250|. 

|–250| + |1250| = 250 + 1250 = 1500.

1500 — 100%

 х — 75%

1500/х = 100/75; х = 1500 • 75 : 100 = 1125

 

3авдання 1046 Відстань між точками:

1) А (4,5) і В (9,5)

АВ = 9,5 – 4,5 = 5

2) С (2,7), OD (0,2)

CD = 2,7 – 0,2 = 2,9

3) М (2,5), ON (4,5)

MN = 4,5 – 2,5 = 2
3авдання 1047

У скільки разів відстань від точки A (–62) до точки М (–7) більша за відстань між точками B (1,4) і С (6 2/5)?

АМ = |–62| – |–7| = 62 – 7 = 55; ВС = 6 2/5 – 1,4 = 6,4 – 1,4 = 5

Отже, відстань між точками А і М більша за відстань між точками В і С у 55 : 5 = 11 разів.

Відповідь: в 11 разів.

 

3авдання 1048

За якого значення a число, що є значенням виразу 2a – 8, є протилежним до себе?

Число, протилежне до себе, — це 0, тому:

2а – 8 = 0

2а = 8

а = 4

Відповідь: якщо а = 4.

 

3авдання 1049 Рівняння

1) ||х| + 2| = 0

    |х|+ 2 = 0;

    |х| = –2

    нема є

    розв’язків

2) ||х| – 5| = 0

    |х| – 5 = 0

    |х| = 5;

    х = 5 або

    х = –5

3) |4 – х| + 128 = 0

    |4 – х| = –128

    нема є

    розв’язків

4) |–х| + 3 = 125

   |–х| = 122

    х = 122 або

    х = –122
3авдання 1050

1) 3 • |х| = |х| + 8

   3 • |х| – |х| = 8

   2|х| = 8

   |х| = 4

   х = 4 або х = –4

2) 2 • |х| – 6 = |–х|

   2 • |х| – 6 = |х|

   2 • |х| – |х| = 6

   |х| = 6

   х = 6 або х = –6

3) 4 • |х – 2| = |2 – х|

   4 • |х – 2| = |–(х – 2)|

   4 • |х – 2| = |х – 2|

   4 • |х – 2| – |х – 2| = 0

   3 • |х – 2| = 0

   х – 2 = 0

   х = 2
3авдання 1051

На координатній прямій (мал. 38) позначено точки, що відповідають числам 1 і a. Перемалюйте малюнок у зошит і позначте точки, що відповідають числам |a|, 2|a|.

3авдання 1052

Знайдіть відстань між точками

1) А(|a – 1| + 4) і B(|–a + 1| + 6);

АВ = (|a – 1| + 6) – (|–a + 1| + 4) = |a – 1| + 6 – |–a + 1| – 4  =

= |a – 1| – |–a + 1| + 6 – 4 = 0 + 2 = 2

2) A(–|a|) і B(|2a|), якщо відстань між точками M (а) і N (–5а) дорівнює 6 і а – додатне число.

За умовою a > 0, тоді MN = |а| + |–5а| = 6a. Якщо а = 1, тоді MN = 6. 
Координата A(–|a|) = A(–1) і B(|2a|) = B(|2 • 1|) = В(2), тому відстань AB = 3

 

3авдання 1053

Якщо а > 0, тоді |а| = а і |а + 2| = а + 2, отже, |а| + |а + 2| – 2 = а + а + 2 – 2 = 2а.

 

3авдання 1054

Із пункту А в протилежних напрямках виїхали два автомобілі. Перший вирушив праворуч від пункту А і їхав зі швидкістю 60 км/год. Другий за 2 год проїхав 100 км ліворуч. Якою буде відстань між автомобілями через 2 год після початку руху?

Розв'язання

1) 60 • 2 = 120 (км) — проїхав за 2 год другий автомобіль;

2) 100 + 120 = 220 (км) — відстань між автомобілями через 2 год.

Відповідь: 220 км.

 

3авдання 1055

Перший велосипедист знаходиться на відстані 15 км від пункту А, другий на відстані (23 - 5) = 18 км, тобто перший на меншій відстані від пункту А.

Відповідь: перший.

Інші завдання дивись тут...

Ім'я:* E-Mail: 2+2/2:*

Додавання коментаря