Завдання 751 Коло
|
1) О центр кола
|
2) ОК або ОР радіус кола
|
3) КР діаметр кола
|
Завдання 752
Відношення довжини кола до довжини його діаметра дорівнює числу пі (l : D = лD : D = л)
Завдання 753
Чи правильно, що коло більшого діаметра має більшу довжину? Так. Відповідь поясніть. Нехай довжина одного кола дорівнює L=2D, а другого кола l=2d. За умовою L > l, тому 2D > 2d й, відповідно, D > d.
Завдання 754
|
1) О центр круга
|
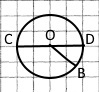
2) ОК або ОР радіус круга
|
3) КР діаметр круга
|
Завдання 755
Круг можна поділити на безліч секторів
Завдання 756
Сума кутів усіх секторів, на які поділено круг, дорівнює: 3) 360°
Завдання 757
Побудуйте коло з центром у точці О й вказаним радіусом: 1) 1,5 см; 2) 2 см; 3) 30 мм. Проведіть його радіус OA і діаметр ВС.
Аналогічно будуємо 1) і 3)
Завдання 758
Побудуйте коло з центром у точці О й радіусом: 1) 1 см; 2) 2,5 см. Проведіть його радіус ОВ і діаметр CD.
1) Побудова кола
Аналогічно будуємо 2)
Завдання 759
|
R
|
2 см
|
0,5 м
|
2 см
|
0,1 дм
|
1 мм | 5 дм |
|
D
|
4 см
|
1 м
|
4 см | 0,2 дм | 2 мм | 10 дм |
|
C
|
12,56 см
|
3,14 м
|
12,56 см | 0,628 дм | 6,28 мм | 31,4 дм |
Завдання 760
1) Якщо радіус кола збільшити у 2 рази, то довжина кола збільшиться у 2 рази
2) Якщо діаметр кола зменшити у 4 рази, то довжина кола зменшиться у 4 рази
Завдання 761
1) Якщо довжину кола збільшити у 3 рази, то радіус кола збільшиться у 3 разів
2) Якщо довжину кола зменшити у 2 рази, то радіус кола зменшиться у 2 рази
Завдання 762
1) Якщо радіус кола зменшити у 3 рази, то довжина кола зменшиться у 3 рази
2) Якщо довжину кола збільшити в 4 рази, то радіус кола збільшиться у 4 рази
Завдання 763
Побудуйте круг з центром у точці О й радіусом: 1) 1,5 см; 2) 2 см; 3) 30 мм. Проведіть його радіус ОМ і діаметр РК.
Круг — частина площини, обмежена колом. Побудова круга аналогічна побудові кола, тому дивись вправу 757.
Завдання 764
Побудуйте круг з центром у точці О й радіусом: 1) 1 см; 2) 2,5 см. Проведіть його радіус ON і діаметр DE.
Круг — частина площини, обмежена колом. Побудова круга аналогічна побудові кола, тому дивись вправу 757.
Завдання 765
|
R
|
4 см
|
1 см
|
6 см
|
4 дм
|
0,2 дм | 0,06 м |
|
D
|
8 см
|
2 см
|
12 см | 8 дм | 0,4 дм | 0,12 дм |
|
C
|
25,12 см
|
6,28 см
|
37,68 см | 25,12 дм | 1,256 дм | 0,3768 дм |
|
S
|
50,24 cм²
|
3,14 см
|
113,04см² | 50,24 дм² | 0,1256 дм² | 0,11304 дм² |
Завдання 766
1) Якщо радіус круга збільшити у 3 рази, то площа круга збільшиться у 9 разів
2) Якщо діаметр зменшити в 4 рази, то площа круга зменшиться у 16 разів
Завдання 767
1) якщо площу круга збільшити в 4 рази, то радіус круга збільшиться в 2 рази
2) якщо площу зменшити в 9 разів, то радіус круга зменшиться в 3 рази
Завдання 768
1) якщо радіус круга зменшити у 3 рази, то площа круга зменшиться у 9 разів
2) якщо площу круга збільшити в 4 рази, то радіус круга збільшиться в 2 рази
Завдання 769
На 4 сектори поділяють круг два діаметри. Побудуйте ці сектори.
Завдання 770
1) якщо круг поділено на 5 рівних секторів, то кут сектора 360° : 5 = 72°
2) якщо круг поділено на 6 рівних секторів, то кут сектора 360° : 6 = 60°
Побудуйте ці сектори.
|
5 рівних секторів
|
6 рівних секторів
|
 |
 |
Завдання 771
Круг поділено на 10 рівних секторів. Знайдіть кут сектора.
Розв'язання
360° : 10 = 36° – кут сектора.
Відповідь: 36°.
Побудуйте ці сектори.
Завдання 772
Знайдіть площу круга, довжина кола якого дорівнює:
|
1) 1) 30л см;
Розв'язання
L = 2лR, звідси
R = L : 2л = 30л : 2л = 15 (см)
S = лR² = л15² = 225л (см²)
Відповідь: 225л см².
|
3) 6,28 см;
Розв'язання
L = 2лR, звідси
R = L : 2л = 6,28 : 2л = 1 (см)
S = лR² = л1² = л (см²)
Відповідь: л см².
|
|
2) 50л см;
Розв'язання
L = 2лR, звідси
R = L : 2л = 50л : 2л = 25 (см)
S = лR² = л25² = 625л (см²)
Відповідь: 225л см².
|
4) 12,56 см.
Розв'язання
L = 2лR, звідси
R = L : 2л = 12,56 : 2л = 2 (см)
S = лR² = л2² = 4л (см²)
Відповідь: 4л см².
|
Завдання 773
Яка площа круга, якщо довжина кола дорівнює 8л см?
Розв’язання
L = 2лR, звідси R = L : 2л = 8л : 2л = 4 (см)
S = лR² = л4² = 16л (см²)
Відповідь: 16л см².
Завдання 774
Обчисліть довжину кола, площа круга якого дорівнює:
|
1) 113,04 см²;
Розв’язання
S = лR², звідси
R² = S : л = 113,04 : 3,14 = 36, R = 6 (см)
L = 2лR = 2 • 3,14 • 6 = 37,68 (см)
Відповідь: 37,68 см.
|
3) 28,26 см²;
Розв’язання
S = лR², звідси
R² = S : л = 28,26 : 3,14 = 9, R = 3 (см²)
L = 2лR = 2 • 3,14 • 3 = 18,84 (см)
Відповідь: 18,84 см.
|
|
2) 78,5 см²;
Розв’язання
S = лR², звідси
R² = S : л = 78,5 : 3,14 = 25, R = 5 (см²)
L = 2лR = 2 • 3,14 • 5 = 31,4 (см)
Відповідь: 31,4 см.
|
4) 225л см².
Розв’язання
S = лR², звідси
R² = S : л = 225л : л = 225, R = 15
L = 2лR = 2 • л • 15 = 30л (см)
Відповідь: 30л см.
|
Завдання 775
Знайдіть довжину кола, якщо площа круга дорівнює 50,24 см²?
Розв’язання
S = лR², звідси R² = S : л = 50,24 : 3,14 = 16, тому R = 4 (см)
L = 2лR = 2 • 3,14 • 4 = 25,12 (см)
Відповідь: 25,12 см.
Завдання 776
1) якщо довжину кола збільшити у 2 рази, то площа круга збільшиться в 4 рази
2) якщо довжину кола зменшити у 3 рази, то площа круга зменшиться в 9 разів
Завдання 777
1) якщо площу круга збільшити в 4 рази, то довжина кола, збільшиться у 2 рази
2) якщо площу круга зменшити в 9 разів, то довжина кола, зменшиться у 3 рази
Завдання 778
Діаметр круглого диска дорівнює 12 см. Знайдіть довжину кола, що обмежує цей диск, і площу цього диска.
Розв’язання
D = 2R, звідси R = D : 2 = 12 : 2 = 6 (см)
L = лD = 3,14 • 12 = 37,68 (см)
S = лR² = 3,14 • 6² = 3,14 • 36 = 113,04 (см²)
Відповідь: 37,68 см; 113,04 см².
Завдання 779
Колесо на відстані 240 м зробило 400 обертів. Знайдіть діаметр колеса (л ≈ 3).
Розв’язання
L = 240 : 400 = 0,6 (м)
L = лD, тому D = L : л = 0,6 : 3 = 0,2 (м)
Відповідь: 0,2 м.
Завдання 780
Діаметр колеса дорівнює 80 см. Скільки повних обертів зробить колесо, якщо автомобіль проїде 150 км (л ≈ 3)?
Розв’язання
80 см = 0,8 м, 150 км = 15 000 м
L = лD = 3 • 0,8 = 2,4 (м)
15 000 : 2,4 = 6250 (об.)
Відповідь: 6250 обертів.
Завдання 781
Круг поділено на сектори. Знайдіть градусні міри кутів цих секторів, якщо вони відносять:
|
1) 2 : 3 : 4;
Розв’язання
Нехай k — коефіцієнт пропорційності. Тоді кут першого сектора дорівнює 2k, кут другого сектора — 3k, а кут третього сектора — 4k. Складаємо рівняння.
2k + 3k + 4k = 360
9k = 360
k = 360 : 9
k = 40
40° • 2 = 80° – перший сектор;
40° • 2 = 120° – другий сектор;
40° • 4 = 160° – третій сектор.
Відповідь: 80°, 120°, 160°.
|
2) 2 : 4 : 5 : 7.
Розв’язання
Нехай k — коефіцієнт пропорційності. Тоді кут першого сектора дорівнює 2k, кут другого сектора — 4k, кут третього сектора — 5k, а кут четвертого сектора — 7k. Складаємо рівняння.
2k + 4k + 5k + 7k = 360
18k = 360
k = 360 : 18
k = 20
20° • 2 = 40° – перший сектор;
20° • 4 = 80° – другий сектор;
20° • 5 = 100° – третій сектор;
20° • 7 = 140° – четвертий сектор.
Відповідь: 40°, 80°, 100°, 140°.
|
Завдання 782
Круг поділено на сектори. Знайдіть градусні міри кутів цих секторів, якщо вони відносяться як 3 : 4 : 5.
Розв’язання
Нехай k — коефіцієнт пропорційності. Тоді кут першого сектора дорівнює 3k, кут другого сектора — 4k, а кут третього сектора — 5k. Складаємо рівняння.
3k + 4k + 5k = 360
12k = 360
k = 360 : 12
k = 30
30° • 3 = 90° – кут першого сектора;
30° • 4 = 120° – кут другого сектора;
30° • 5 = 150° – кут третього сектора;
Відповідь: 90°, 120°, 150°.
Завдання 783
Чи можна стверджувати, що рівні сектори мають рівні площі? Можна, бо рівні сектори мають однакові кути і радіуси.
Завдання 784
Чи існує круг, у якого площа виражається таким самим числом, що й довжина кола (найменування величин не враховувати)? Існує. Якщо радіус дорівнює 2.
S = лR² = л2² = 4л і L = 2лR = 2 • л • 2 = 4л, тому S = L
Завдання 785
Чи можна вирізати з квадрата 2 х 2 дм круг, довжина кола якого дорівнює 9,42 дм?
Розв’язання
L = лD, звідси D = L : л = 9,42 : 3,14 = 3 (дм)
2 дм < 3 дм
Відповідь: не можна.
Завдання 786
1) Обчисліть площу зафарбованої фігури на цих малюнках (л ≈ 3)
Розв’язання
1) R = 5 : 2 = 2,5 (см) – радіус більшого круга.
2) S1 = 2,5² • л = 6,25 • 3 = 18,75 (см²) – площа більшого круга.
3) r = 3 : 2 = 1,5 (см) – радіус меншого круга.
4) S2 = 1,5² • л = 2,25 • 3 = 6,75 (см²) – площа меншого круга.
5) Sпр. = 5 • 3 = 15 (см²) – площа прямокутника.
6) S = S1 + S2 + Sпр. = 18,75 + 6,75 + 15 = 40,5 (см²)
Відповідь: 40,5 см².
2) Обчисліть площу зафарбованої фігури на другому малюнку (л ≈ 3)
Розв’язання
1) Sкв. = 6 • 6 = 36 (см²) – площа квадрата.
2) Sсектора = 6² • л : 4 = 27 (см²) – площа сектора круга
3) Sчастини = Sкв. - S сектора = 36 – 27 = 9 (см²) – площа верхньої або нижньої частини
4) S = Sкв. - 2Sчастина = 36 – 2 • 9 = 36 – 18 = 18 (см²)
Відповідь: 18 см².
Завдання 787
Із аркуша паперу вирізано круг. Як, перегинаючи аркуш, знайти центр цього круга? Зігнути круг навпіл по діагоналі, а потім ще раз по радіусу, тобто центр круга є на перетині двох перегинів круга.
Завдання 788
Яка клумба для квітів має більшу площу: та, що має форму квадрата зі стороною 4 м, чи та, що має форму круга з діаметром 4 м?
Розв’язання
1) Sкв. = 4 • 4 = 16 (м²) – площа квадрата зі стороною 4 м.
2) 4 : 2 = 2 (м) – радіус круга.
3) Sкруга = 2² • 3,14 = 12,56 (м²) – площа круга з діаметром 4 м.
12,56 < 16
Відповідь: більша та клумба, що має форму квадрата зі стороною 4 м.
Завдання 789
Бабуся пошила нову скатертину на обідній круглий стіл.
1) Скільки метрів тканини завширшки 2 м витратила бабуся, якщо діаметр скатертини — 1 м?
Розв’язання
2 • 1 = 2 (м)
Відповідь: 2 метри.
2) Чи вистачило бабусі 3,5 м мережива, щоб оздобити скатертину по краю?
Розв’язання
L = 2D = 2 • 1 = 2 (м) – потрібно мережива.
2 < 3,5, тому вистачить мережива.
Відповідь: вистачить.