Інші завдання дивись тут...

Завдання 951 Лінійна функція

1) у = 3x – 2; Так, k = 3, b = –2 2) у = 8 – 7x; Так, k = –7, b = 8 3) у = x/3 + 2; Так, k = 1/3, b = 2 4) у = 3/x + 2; Ні 5) у = 2x² + 4; Ні

6) y = (12x – 8)/4; Так, k = 3, b = –2 7) у = x/5; Так, k = 1/5, b = 0 8) у = –4; Так, k = 0, b = –4 9) у = 0? Так, k = 0, b = 0

Завдання 952 Прямопропорційна функція

1) у = 4x; Так, k = 4 2) у = 4/x; Ні

3) y = x/4; Так, k = 1/4 4) у = 0; Ні

5) у = –4x; Так, k = –4 6) y = –x/4? Так, k = –1/4

Завдання 953

Лінійна функція задана формулою у = 6x – 5.  Заповнили таблицю:

x	–3	–2	–1	0	1	2	3
y	–23	–17	–11	–5	1	7	13
	у = 6 • (–3) – 5 = –16 – 5 = –23 у = 6 • (–2) – 5 = –12 – 5 = –17 у = 6 • (–1) – 5 = –6 – 5 = –1			у = 6 • 0 – 5 = –5 у = 6 • 1 – 5 = 6 – 5 = 1 у = 6 • 2 – 5 = 12 – 5 = 7 у = 6 • 3 – 5 = 18 – 5 = 13

Завдання 954

Функцію задано формулою у = –2x + 5. Знайдіть:

1) значення функції, якщо: х = –4; у = –2 • (–4) + 5 = 8 + 5 = 13 х = 3,5; у = –2 • 3,5 + 5 = –7 + 5 = –2 х = 0; у = –2 • 0 + 5 = 5

2) значення аргументу, якщо: у = 9; –2х + 5 = 9; –2х = 4; х = –2 у = –5; –2х + 5 = –5; –2х = –10; х = 5 у = 0; –2x + 5 = 0; –2x = –5; х = 2,5

Завдання 955

Функцію задано формулою у = 0,4x + 3. Заповнили таблицю:

x	–2	–12,5	0	–7,5	5	–40
y	2,2	–2	3	0	5	–13
	у = 0,4 • (–2) + 3 = –0,8 + 3 = 2,2 –2 = 0,4х + 3; 0,4х = –5; х = –12,5 у = 0,4 • 0 + 3 = 3			0 = 0,4х + 3; 0,4х = –3; х = –7,5 у = 0,4 • 5 + 3 = 2 + 3 = 5 –13 = 0,4х + 3; 0,4х = –16; х = –40

Завдання 956

Функцію задано формулою у = 0,3x – 2. Знайдіть:

1) значення функції, якщо:

х = 5; у = 0,3 • 5 – 2 = 1,5 – 2 = –0,5

х = –2, у = 0,3 • (–2) – 2 = –0,6 – 2 = –2,6

х = 0. у = 0,3 • 0 – 2 = –2
2) значення аргументу, якщо:

у = 1; 0,3х – 2 = 1; 0,3х = 1 + 2; 0,3х = 3; х = 10

у = –11; 0,3х – 2 = –11; 0,3х = –11 + 2; 0,3х = –9; х = –30

у = 0,8. 0,3х – 2 = 0,8; 0,3х = 2,8; 3/10 х = 28/10; х = 28/3 = 9 1/3

 

Завдання 957

Заповніть таблицю та побудуйте графік функції:

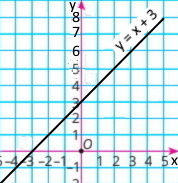
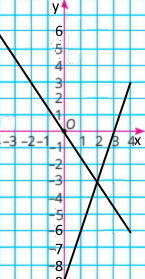
1) у = х + 3 x 0 1 y 3 4	2) у = 1/3 x – 5 x 0 3 y –5 –4

Завдання 958

Заповніть таблицю та побудуйте графік функції:

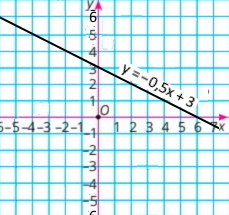
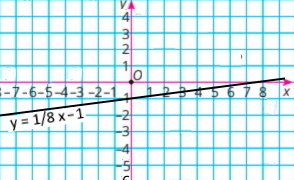
1) у = 3 – 0,5x x 0 2 y 3 2	2) y = 1/8 x – 1 x 0 8 y –1 0

Завдання 959

Заповніть таблицю та побудуйте графік функції:

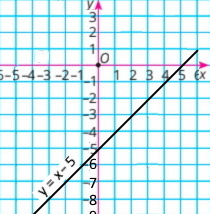
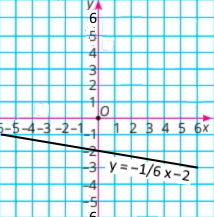
1) у = x – 5 x 0 5 y –5 0	3) y = –1/6 x – 2 x 0 6 y –2 –3
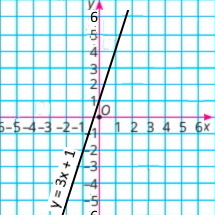
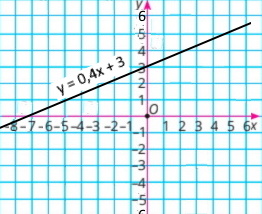
2) у = 3x + 1 x 0 1 y 1 4	4) у = 0,4x + 3 x 0 5 y 3 5

Завдання 960

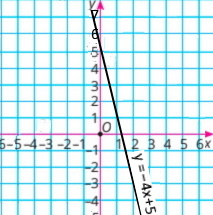
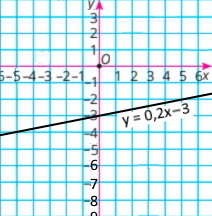
1) у = 4 – x x 0 1 y 4 3	2) у = –4x + 5 x 0 1 y 5 1	2) у = 0,2x – 3 x 0 5 y –3 –2

Завдання 961

Функцію задано формулою y = 1/3х.Знайдіть:

1) значення функції, якщо:

х = 6; у = 1/3х = 1/3 • 6 = 2

х = –3; у = 1/3х = 1/3 • (–3) = –1
х = –3,2. у = 1/3х = 1/3 • (–3,2) = 1/3 • (–3 1/5) = 1/3 • (–16/5) = –16/15 = –1 1/15

2) значення аргументу, якщо:

у = –2; 1/3х = –2; х = –2 : 1/3; х = –2 • 3; х = –6

у = 1/3х; 1/3х = 1/3; х = 1/3 : 1/3; х = 1/3 • 3; х = 1

у = 12. 1/3х = 12; х = 12 : 1/3; х = 12 • 3; х = 36

 

Завдання 962

Функцію задано формулою у = 0,6x. Заповніть таблицю:

x	10	0,6	–5	–1,2	8	–100	5/9
y	6	0,36	–3	–0,72	4,8	–60	1/3
	у = 0,6 • 10 = 6 у = 0,6 • 0,6 = 0,36		у = 0,6 • (–5) = –3 у = 0,6 • (–1,2) = –0,72		4,8 = 0,6х; х = 4,8 : 0,6 = 8 –60 = 0,6х; х = –60 : 0,6 = 100 1/3 = 0,6х; х = 1/3 : 6/10 = 1/3•5/3 = 5/9

Завдання 963

Функцію задано формулою у = 1,2x. Знайдіть:

1) значення функції, якщо: х = 10; у = 1,2х = 1,2 • 10 = 12 х = 0,6; у = 1,2х = 1,2 • 0,6 = 0,72 x = –5; у = 1,2х = 1,2 • (–5) = –6 х = –4. у = 1,2х = 1,2 • (–4) = –4,8

2) значення аргументу, якщо: у = 3,6; 1,2х = 3,6; х = 3 у = –2,4; 1,2х = –2,4; х = –2 у = 6; 1,2х = 6; х = 5

Завдання 964 Графіки прямої пропорційності

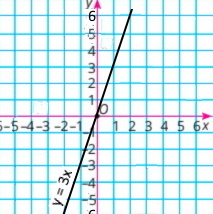
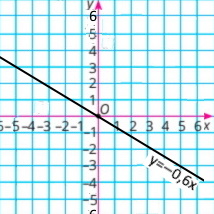
1) у = 3х x –1 1 y –3 3	3) y = –0,6x x –5 5 y 3 –3
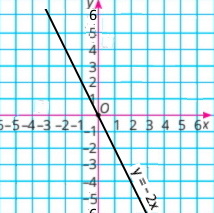
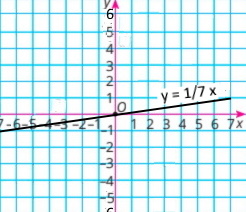
2) у = –2x x –1 1 y 2 –2	4) у = 1/7 x x –7 7 y –1 1

Завдання 965 Графіки прямої пропорційності

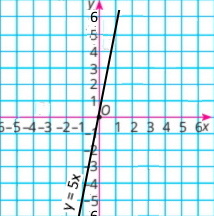
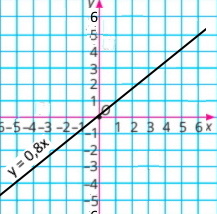
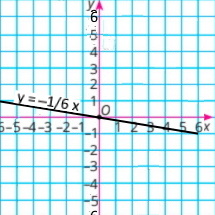
1) у = 5x x –1 1 y –5 5	2) у = 0,8x x –5 5 y –4 4	2)  у = –1/6х x –6 8 y 1 –1

Завдання 966

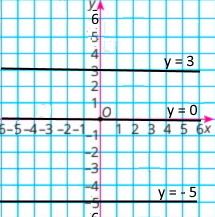
Побудуйте в одній системі координат графіки лінійних функцій: у = 3; у = –5; у = 0.

Завдання 967

Без побудови графіка функції у = 1,8x – 3, визначте, через які з точок проходить графік.

1) А(–2;–6,6). у = 8,8 • (–2) – 3 = –3,6 – 3 = –6,6. Точка А належить графіку.

2) В(1;1,2). у = 1,8 • 1 – 3 = 1,8 – 3 = –1,2. Точка В не належить графіку.

3) С(0;–3). у = 1,8 • 0 – 3 = –3. Точка С належить графіку.
4) D(5;7). y = 1,8 • 5 – 3 = 9 – 3 = 6. Точка D не належить графіку.

 

Завдання 968

Не виконуючи побудови, визначте, чи належить графіку функції у = 8x – 14 точки:

1) А(–1;–6). у = 8 • (–1) – 14 = –8 – 14 = –22. Точка А не належить графіку.

2) В(2;2). у = 8 • 2 – 14 = 16 – 14 = 2. Точка В належить графіку.

 

Завдання 969

1) Функція прямої пропорційності у = kx.

Точка (8;4) належить графіку, тому 4 = 8k, k = 1/2, отже, функція у = 1/2 х.

x	8	6	2	1	1/2	0	–1	–2	–3	–4
y	4	3	1	1/2	1/4	0	–1/2	–1	–1 1/2	–2
	у = 1/2 • 6 = 3 у = 1/2 • 2 = 1 у = 1/2 • 1 = 1/2 у = 1/2 • 1/2 = 1/4					у = 1/2 • 0 = 0 у 1/2 • (–1) = –1/2 у = 1/2 • (–2) = –1   у = 1/2 • (–3) = –3/2 = –1 1/2

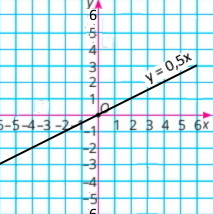
2) Формула функції: y = 1/2x або у = 0,5х.

Для побудови графіка достатньо провести пряму через, дві точки, наприклад, з координатами (–2;–1) і (2;1).

Завдання 970, 971

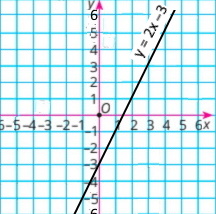
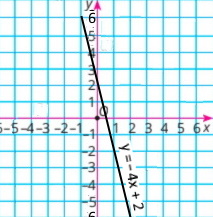
у = 2x – 3 x 0 2 y –3 1	у = 2 – 4x x 0 1 y 2 –2
1) у(4) = 5; y(–1) = –5; y(0,5) = –2; 2) якщо у = 1, то x = 2;     якщо у = –1, то х = 1;     якщо у = 0, то х = 1,5; 3) функція набуває додатних значень:     у > 0 при х > 1,5.	1) у(1) = –2; у(0) = 2; у(–2) = 10; 2) якщо у = –4, то х = 1,5;     якщо у = –2, то х = 1;     якщо у = 2, то х = 0; 3) функція набуває від'ємних значень:      у < 0 при х > 0,5.

Завдання 972, 973

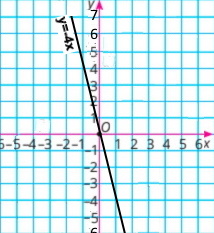
у = 0,5x x –4 4 y –2 2	у = –4x x –1 1 y 4 –4
1) y(4) = 2; y(–6) = –3; y(3) = 1,5; 2) якщо у = 2,5, то х = 5;    якщо у = –2, то х = –4;    якщо у = 1, то х = 2; 3) функція набуває від’ємних значень:     у < 0 при х < 0	1) у(2) = –8; у(–1) = 4: у(0,5) = –2; 2) якщо у = –4, то х = 1;     якщо у = 2, то х = –0,5; 3) функція набуває додатних значень:     у > 0 при х < 0

Завдання 974, 975

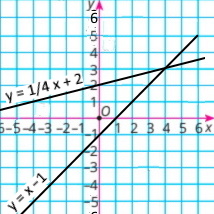
Побудуйте в одній системі координат графіки функцій у = x –1 і y = 1/4x + 2 та знайдіть координати точки їхнього перетину.

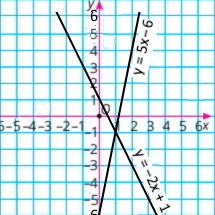
у = x –1 і y = 1/4x + 2		в) у = 5x – 6 і у = –2x + 1
х 0 1 у 1 0	х 0 4 у 2 3	х 0 2 у –6 4	х 0 1 у 1 –1
Координати точки перетину (4;3)		Координати точки перетину (1;–1)

Завдання 976 

Без побудови, знайдіть координати точок перетину з осями координат графіка функції:

1) у = 2,5x + 10;

3 віссю 0х (у = 0): 2,5x + 10 = 0; 2,5х = –10; х = –4;

Графік перетинається з віссю абсцис в точці з координатами (–4;0);

з віссю 0у (х = 0): у = 2,5х + 10 = 2,5 • 0 + 10 = 10; 

Графік перетинається з віссю ординат в точці з координатами (0;10);

2) у = 6x – 4.

3 віссю 0х (у = 0): 6х – 4 = 0; х = 2/3; 

Графік перетинається з віссю абсцис в точці з координатами (2/3;0);

з віссю 0у (х = 0): у = 6х – 4 = 6 • 0 – 4 = –4;

Графік перетинається з віссю ординат в точці з координатами (0; 10).

 

Завдання 977

Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:

1) у = 2x – 4;

3 віссю 0х (у = 0): 2/3х – 4 = 0; 2/3 х = 4; х = 4 : 2/3 = 12/2 = 6;

Графік перетинається з віссю абсцис в точці з координатами (6;0);
з віссю 0у (х = 0): у= 2/3х – 4 = 2/3 • 0 – 4 = –4;

Графік перетинається з віссю ординат в точці з координатами (0;–4);

2) у = 7 – 3x.

З віссю 0х (у = 0): 7 – 3х = 0; х = 7/3 = 2 1/3;

Графік перетинається з віссю абсцис в точці з координатами (2 1/3;0);

з віссю 0y (х = 0): у = 7 – 3х = 7 – 3 • 0 = 7;

Графік перетинається з віссю ординат в точці з координатами (0;7).

 

Завдання 978

Не виконуючи побудови графіка функції у = 2x – 9, знайдіть точку цього графіка, у якої:

1) абсциса дорівнює ординаті;

Якщо у = х, тоді x = 2x – 9; x = 9. Точка з координатами (9;9);

2) ордината на 6 більша за абсцису.

Якщо у = х + 6, тоді х + 6 = 2х – 9; х = 15. Точка з координатами (15;21).

 

Завдання 979

Не виконуючи побудови графіка функції у = –7x + 8, знайдіть точку цього графіка, у якої абсциса та ордината — протилежні числа.

Якщо у = –х, тоді –x = –7х + 8; 6х = 8; х = 8/6 = 1 1/3. 

Точка з координатами (1 1/3; –1 1/3).

 

Завдання 980

Не виконуючи побудови, знайдіть координати точок перетину графіків функцій:

1) у = 3,7x + 10 і у = 1,4x – 13 3,7х + 10 = 1,4х – 13 3,7х – 1,4х = –13 – 10 2,3х = –23 х = –23 : 2,3 х = –10 у = 3,7 • (–10) + 10 = –37 + 10 = –27 Точка з координатами (–10;–27)

2) у = 4 – 2/7 x і у = 9/7 x + 26 4 – 2/7 х = 9/7 х + 26 9/7 х  + 2/7 х = 4 – 26 11/7х = –22 х = –22 : 11/7 х = –14 у = 4 – (–2/7) • (–14) = 8 Точка з координатами (–14;8)

Завдання 981

Не виконуючи побудови, знайдіть координати точок перетину графіків функцій

у = 4x – 7 і у = –2x + 11.

4x – 7 = –2x + 11

4x + 2х = 11 + 7

6x = 18
x = 3
–y = 4 • 3 – 7 = 12 – 7 = 5

Графіки цих функцій перетинаються в точці з координатами (3;5).

 

Завдання 982, 983

При якому значенні змінної x функції набувають рівних значень?

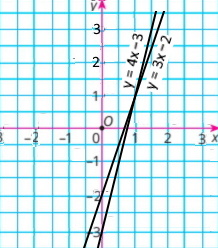
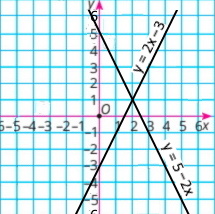
f(x) = 4x – 3 і g(x) = 3x – 2 4x – 3 = 3х – 2 4x – 3х = –2 + 3  х = 1 Тоді у = 4 • 1 – 3 = 1. У точці з координатами (1;1).		f(x) = 5 – 2x і g(x) = 2x – 3 5 – 2х = 2х – 3 4х = 8 x = 2 Тоді у = 5 – 2 • 2 = 1. У точці з координатами (2;1).
х 0 2 у –3 5	х 0 2 у –2 4	х 0 2 у 5 1	х 0 2 у –3 1
1) f(x) > g(x) при значеннях х > 1; 2) f(x) < g(x) при значеннях х < 1.		1) f(x) < g(x) при значеннях х > 2 2) f(х) > g(x) при значеннях x < 2

Інші завдання дивись тут...