
Завдання 876
Прочитайте запис, укажіть аргумент функції та залежну змінну:
1) s(t) = 70t; t – аргумент; s – залежна змінна
2) у(x) = –2x + 4; х – аргумент; у – залежна змінна
3) V(a) = a3; а – аргумент; V – залежна змінна
4) f(x) = x² –4. х – аргумент; f – залежна змінна
Завдання 877
Функцію задано формулою у = 10x + 1. Знайдіть значення у:
1) якщо х = –1, тоді у = 10x + 1 = 10 • (–1) + 1 = –10 + 1 = –9
2) якщо х = 3, тоді у = 10x + 1 = 10 • 3 + 1 = 30 + 1 = 31
3) якщо x = –1/5, тоді у = 10x +1 = 10 • (–1/5) + 1 = –2 + 1 = –1
4) якщо x = 7, тоді у = 10x + 1 = 10 • 7 + 1 = 70 + 1 = 71
Завдання 878
Функцію задано формулою f (x) = 3 – 4x. Чи є правильною рівність:
1) f (–2) = –5; Ні, бо f(–2) = 3 – 4 • (–2) = 3 + 8 = 11
2) f(1/2) = 1; Так, бо f(1/2) = 3 – 4 • 1/2 = 3 – 2 = 1
3) f (0) = –1; Ні, бо f(0) = 3 – 4 • 0 = 3
4) f (–1) = 7? Так, бо f(–1) = 3 – 4 • (–1) = 3 + 4 = 7
Завдання 879
Функцію задано формулою f(x) = 7x – 5. Знайдіть:
|
1) f(2) = 7 • 2 – 5 = 9 2) f(0) = 7 • 0 – 5 = –5 |
3) f(–3) = 7 • (–3) – 5 = –26 4) f(200) = 7 • 200 – 5 = 1395 |
Завдання 880
Функцію задано формулою f(x) = 2x² – 1. Чи є правильною рівність:
1) f(1) = 1; Так, бо f(1) = 2 • 1² – 1= 1
2) f(4) = 15; Ні, бо f(4) = 2 • 4² – 1= 31
3) f(–2) = –9; Ні, бо f(–2) = 2 • (–2)² – 1= 7
4) f(0) = 0; Ні, бо f (0) = 2 • 0² – 1= 1
5) f(–1) = 1; Так, бо f(–1) = 2 • (–1)² – 1= 1
6) f(–5) = 19? Ні, бо f(–5) = 2 • (–5)² – 1= 49
Завдання 881
Функцію задано формулою y = x² – 3. Знайдіть значення y:
1) якщо х = 5, тоді у = х² – 3 = 5² – 3 = 25 – 3 = 22
2) якщо х = –4, тоді у = х² – 3 = (–4)² – 3 = 16 – 3 = 13
3) якщо х = 0,1, тоді у = х² – 3 = 0,1² – 3 = 0,01 – 3 = –2,99
4) якщо х = 0, тоді у = х² – 3 = 0² – 3 = –3
Завдання 882
Функцію задано формулою f (x) = 3 + 4x. Знайдіть значення x, при якому:
1) f(x) = 19; 3 + 4x = 19; 4x = 16; x = 4
2) f(x) = –3; 3 + 4x = –3; 4x = –6; x = –3/2 = –1 1/2
3) f(x) = 0; 3 + 4x = 0; 4x = –3; x = –3/4
4) f(x) = 323. 3 + 4x = 323; 4x = 320; x = 80
Завдання 883
Функцію задано формулою f (x) = –0,1x – 2. Знайдіть значення x, при якому:
1) f(x) = 1; –0,1x – 2 = 1; –0,1x = 3; x = –30
2) f(x) = –100; –0,1x – 2 = –100; –0,1x = –98; x = 980
3) f(x) = –43,6. –0,1x – 2 = –43,6; –0,1x = –41,6; x = 416
Завдання 884
Функцію задано формулою y = –1/6x + 2. Знайдіть:
1) значення функції для значень аргументу:
|
f(12) = –1/6 • 12 + 2 = 0 f(6) = –1/6 • 6 + 2 = 1 f(–6) = –1/6 • (–6) + 2 = 3 f(0) = –1/6 • 0 + 2 = 2 |
f(1) = –1/6 • 1 + 2 = 1 5/6 f(2) = –1/6 • 2 + 2 = 1 2/3 f(–4) = –1/6 • (–4) + 2 = 2 2/3 f(–3) = –1/6 • (–3) + 2 = 2 1/2 |
2) значення аргументу, при якому значення функції:
у = 4, якщо –1/6x + 2 = 4; –1/6x = 2; x = –12
у = 3, якщо –1/6x + 2 = 3; –1/6x = 1; x = –6
у = 0, якщо –1/6x + 2 = 0; –1/6x = –2; x = 12
у = –1, якщо –1/6x + 2 = –1; –1/6x = –3; x = 18
Завдання 885
Функцію задано формулою f(x) = 2x – 1.
1) f(3) = 2 • 0 – 1 = 6 – 1 = 5
f(–4) = 2 •(–4) – 1 = –8 – 1 = –9
f(0) = 2 • 0 – 1 = –1
f(–0,5) = 2 • (–0,5) – 1 = –1 – 1 = –2
f(3,2) = 2 • 3,2 – 1 = 6,4 – 1 = 5,4
2) Знайдіть значення x при якому:
f(x) = 7, якщо 2x – 1 = 7; 2x = 8; x = 4
f(x) = –9, якщо 2x – 1 = –9; 2x = –8; x = –4
f(x) = 0, якщо 2x – 1 = 0; 2x = 1; x = 0,5
f(x) = –2,4, якщо 2x – 1 = –2,4; 2x = –1,4; x = –0,7
3) Чи є правильною рівність:
f(5) = 9; Так, бо f(5) = 2 • 5 – 1 = 9
f(0,3) = 0,4; Ні, бо f(0,3) = 2 • 0,3 – 1 = –0,4, отже, f(0,3) ≠ 0,4
f(–3) = –7? Так, бо f(–3) = 2 • (–3) – 1 = –7
Завдання 886
Функцію задано формулою y = x (x + 8). Заповніть таблицю:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
–15 |
–12 |
–7 |
0 |
9 |
20 |
33 |
Завдання 887
Функцію задано формулою y = –2/3х. Заповніть таблицю:
|
x |
–9 |
–6 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
6 |
|
y |
6 |
4 |
2 |
1 1/3 |
2/3 |
0 |
–2/3 |
–1 1/3 |
–2 |
–4 |
Завдання 888
Функцію задано формулою y = х² + x + 1. Заповніть таблицю:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
4 |
7 |
|
y |
–11 |
–5 |
–1 |
0 |
3 |
7 |
21 |
57 |
Завдання 889
Кожному натуральному числу, яке більше за 10, але менше від 20, поставили у відповідність остачу при діленні цього числа на 6.
1) Яким способом задано цю функцію? Цю функцію задано описом.
2) Яка область значень цієї функції? областю значень є множина цілих чисел від 0 до 5.
3) Задайте цю функцію табличним способом.
|
x |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
y |
5 |
0 |
1 |
2 |
3 |
4 |
5 |
0 |
1 |
Завдання 890
Область визначення деякої функції — усі двоцифрові натуральні числа, які кратні 10, а значення функції у 5 разів менші від відповідних значень аргументу. Задайте цю функцію формулою та табличним способом.
y = x/5, де x = 10k, k = 1…9.
|
x |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
y |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
Завдання 891
Область визначення деякої функції — одноцифрові натуральні числа, а значення функції у 2 рази більші за відповідні значення аргументу.
1) Яким способом задано цю функцію? Функцію задано описом.
2) Задайте цю функцію формулою та табличним способом. у = 2х, де 1 ≤ х ≤ 9.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
y |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
Завдання 892
Задайте формулою функцію, якщо значення функції:
1) протилежні відповідним значенням аргументу; y = –x
2) дорівнюють потроєним відповідним значенням аргументу; y = 3x
3) на 4 більші за квадрати відповідних значень аргументу. y = x² + 4
Завдання 893
Задайте формулою функцію, якщо значення функції:
1) на 3 менші від відповідних значень аргументу; y = x – 3
2) на 5 більші за подвоєні відповідні значення аргументу. y = 2x + 5
Завдання 894
Із кроком 0,5 таблиця значень функції у = x² + 2x, де –1 ≤ x ≤ 3.
|
x |
–1 |
–0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y |
–1 |
–0,75 |
0 |
1,25 |
3 |
5,25 |
8 |
11,25 |
15 |
Завдання 895
Із кроком 1 таблиця значень функції y = x3 – 1, де –3 ≤ x ≤ 2.
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
|
y |
–28 |
–9 |
–2 |
–1 |
0 |
7 |
Завдання 896
Функцію задано формулою у = 0,2x – 5.
|
x |
4 |
35 |
–1,5 |
18 |
–3 |
|
y |
–4,2 |
2 |
–5,3 |
–1,4 |
–5,6 |
Завдання 897
Дано функцію у = 8 – x.
|
x |
14 |
56 |
–1,4 |
–7 |
|
y |
6 |
0 |
8,2 |
9 |
Завдання 898
Дано функції g(x) = 20/x – 3 і h (x) = 8 – 3x. Порівняйте:
1) g(1)= 20/1 – 3 = 17; h(1) = 8 – 3 • 1 = 5; g(1) > h(1)
2) g(5) = 20/5 – 3 = 1; h(2) = 8 – 3 • 2 = 2; g(5) < h(2)
3) g(–2) = 20/–2 – 3 = –13; h(6) = 8 – 3 • 6 = –10; g(–2) < h(6)
Завдання 899
Функція f(x) = {–2x+1, якщо x ≤ –2; x², якщо –2 < x < 3; 6, якщо x ≥ 3. Знайдіть:
1) f(–3) = –2 • (–3) + 1 = 7
2) f(–2) = –2 • (–2) + 1 = 5
3) f(2) = 2² = 4
4) f(3) = 6
5) f(2,9) = 2,9² = 2,9 • 2,9 = 8,41
6) f(8,1) = 6
Завдання 900
Функція y = {–2x + 4, якщо x > 0, 0,1x – 5, якщо x ≤ 0, яка відповідає аргументу:
1) 3; y(3) = –2 • 3 + 4 = –2
2) 0,001; y(0,001) = –2 • 0,001 + 4 = 3,998
3) 0; у(0) = 0,1 • 0 – 5 = –5
4) –8. y(–8) = 0,1 • (–8) – 5 = –5,8.
Завдання 901
Функцію задано за допомогою таблиці:
|
x |
2 |
4 |
6 |
8 |
|
y |
5 |
7 |
9 |
11 |
1) Область визначення – множина парних натуральних чисел;
2) Задання функції описом: функція кожному парному натуральному числу ставить у відповідність число, більше на 3 від аргументу; задання функцїї формулою: у = х + 3, де х – парне натуральне число.
Завдання 902
Функцію задано за допомогою таблиці:
|
x |
1 |
3 |
5 |
7 |
9 |
|
y |
0,5 |
1,5 |
2,5 |
3,5 |
4,5 |
1) Область визначення – множина непарних натуральних чисел;
2) задання функції описом: функція кожному непарному натуральному числу ставить у відповідність число, вдвічі менше від аргументу.
задання функції формулою: у = х/2, де х – непарне натуральне число.
Завдання 903
Функції задано формулами y = x² – 8x і у = 4 – 8x. При яких значеннях аргументу ці функції набувають рівних значень?
x² – 8х = 4 – 8х
x² = 4
(х – 2)(х + 2) = 0
х = 2 або х = –2
Відповідь: при х = –2 або х = 2 функції набувають рівних значень.
Завдання 904
Функцію задано формулою f(x) = 3x + 5. При якому значенні x значення функції дорівнює значенню аргументу?
3х + 5 = х
2х = –5
х = –2,5
Відповідь: при х = –2,5 значення даної функції дорівнює значенню аргументу.
Завдання 905
Функцію задано формулою y = x² + 2x – 1. При яких значеннях x значення функції дорівнює подвоєному значенню аргументу?
х² + 2х – 1 = 2х
х² = 1
(х – 1)(х + 1) = 0
х = 1 або х = –1
Відповідь: при х = 1 або х = –1 значення даної функції дорівнює подвійному значенню аргументу.
Завдання 906
Функцію f задано описом: значення функції дорівнює найбільшому цілому числу, яке не більше за відповідне значення аргументу.
f(3,7) = 3; f(0,64) = 0; f(2) = 2; f(–0,35) = –1; f(–2,8) = –3
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 907
Цього року фермер скоротив площу під капусту на 10 %. Урожайність капусти цього року підвищилася на 12 % порівняно з минулим роком. Збільшився чи зменшився врожай капусти порівняно з минулим роком і на скільки відсотків?
Початкова площа була x, а урожайність була y, отже, врожай капусти дорівнює ху.
Цього року площу скоротили на 10 %, тому стала 0,9x, а урожайність збільшилась
на 12%, тому стала 1,12y, отже, врожай капусти дорівнює 0,9x • 1,12y = 1,008xy.
1,008xy – ху = 0,008, або, помноживши результат на 100%, одержимо 0,8%.
Відповідь: у цьому році капусти зібрано на 0,8% більше.
Завдання 908 Рівняння
|
1) 3,4(1 + 3x) – 1,2 = 2(1,1 + 5,1х) 10,2х – 10,2х = 2,2 + 1,2 – 3,4 |
3) 3(|х – 1| – 6) + 21 = 0 |
|
2) |2х – 1| = 17,3 Два корені |
4) 0,2(7 – 2x) = 2,3 – 0,3(x – 6) |
Завдання 909
Дано три числа, з яких кожне наступне на 10 більше за попереднє. Знайдіть ці числа, якщо добуток найбільшого та середнього з них на 320 більший за добуток найбільшого та найменшого із цих чисел.
Розв'язання
Нехай дано три числа х – 10, х і х + 10. Складаємо рівняння:
(х + 10)х – 320 = (х + 10)(х – 10)
х² + 10х – 320 = х² – 100
10х = 220
х = 22 – середнє число;
22 – 10 = 12 – попереднє число;
22 + 10 = 32 – наступне число.
Відповідь. 12, 22, 32.
Завдання 910
Доведіть, що коли a + c = 2b, то a² + 8bc = (2b + c)².
За умовою а + с = 2b, звідси а = 2b – с.
а² + 8bс = (2b – с)² + 8bс = 4b² – 4bс + с² + 8bс = 4b² + 4bс + с² = (2b + с)².
Завдання 911
Відомо, що x + y = a²/4 , у + z = –a, x + z = 1. Доведіть, що вираз x + у + z набуває тільки невід’ємних значень.
Додамо ці вирази почленно:
x + y + у + z + x + z = a²/4 + (–a) + 1
2(х + y + z) = a²/4 – а + 1
2(х + y + z) = (a/2 – 1)².
Отриманий вираз невід'ємний, а, отже, і сума х + у + z – невід'ємна.
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
Завдання 912
Побудуйте пряму, яка проходить через точки A(–2;3) і B(4;3).
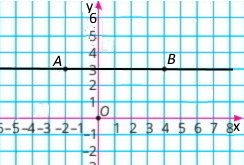
Ординати точок прямої дорівнюють 3.
Завдання 913
Побудуйте пряму, яка проходить через точки C(3;0) і D(3;–4).
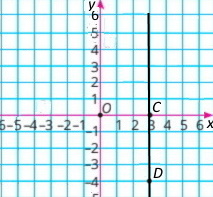
Абсциси точок прямої дорівнюють 3.
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
Завдання 914
Доведіть, що в будь–якому 60–цифровому числі, десятковий запис якого не містить нулів, можна закреслити кілька цифр таких, що отримане в результаті цього число буде ділитися націло на 1001. За умовою задачі в записі числа відсутні нулі, тому хоча б одна цифра в записі присутня мінімум 6 разів. Закреслимо цифри у записі таким чином, щоб утворилося число вигляду хххххх, де х – цифра від 1 до 9. Перетворимо це число: хххххх = 1000 ххх + ххх = 1001 ххх. Бачимо, що це число ділиться без остачі на 1001. Твердження задачі доведено.