Завдання 1056 Лінійне рівняння з двома змінними
|
1) 7х + 11у = 36 Так 2) x² + 4y = 6 Ні |
3) 12х – 17у = 0 Так 4) –3х + ху = 10 Ні |
Завдання 1057
|
1) 8x – 0,9y = 1/6 Так 2) х – 4у² = 5 Ні |
3) 6х + 2ху = 9 Ні 4) 3х + 4у = 0 Так |
Завдання 1058
Які з пар чисел є розв’язками рівняння 3х – 7у = 14?
Пара чисел (7;1) є розв’язком, бо 3 • 7 – 7 • 1 = 21 – 7 = 14
Пара чисел (0;–2) є розв’язком, бо 3 • 0 – 7 • (–2) = 0 + 14= 14
Пара чисел (8;2) не є розв’язком, бо 3 • 8 – 7 • 2 = 24 – 14 = 10. 10 ≠ 14
Пара чисел (–7;–5) є розв’язком, бо 3 • (–7) – 7 • (–5) = –21 + 35 = 14
Пара чисел (10;3) не є розв’язком, бо 3 • 10 – 7 • 3 = 30 – 21 = 9. 9 ≠ 14
Завдання 1059
Розв’язком якого з рівнянь є пара чисел (3;–2):
1) 4x + 5у = 2; Є розв’язком, бо 4 • 3 + 5 • (–2) = 12 – 10 = 2
2) 3x – 2у = 5; Не є розв’язком, бо 3 • 3 – 2 • (–2) = 9 + 4 = 13
3) 0,2x – 0,5у = 1,6. Є розв’язком, бо 0,2 • 3 – 0,5 • (–2) = 1,6
Завдання 1060
Чи є розв’язком рівняння 2х – 9у = 13 пара чисел:
1) Пара чисел (2,5;2) не є розв'язком, бо у = 2 • 2,5 – 9 • 2 = –13
2) Пара чисел (10,5;2) не є розв'язком, бо 2х • 10,5 – 9 • 2 = 3
3) Пара чисел (5;–1/3) є розв'язком, бо 2 • 5 + 9 • (–1/3) = 10 + 3 = 13
4) Пара чисел (–7;–3) є розв'язком, бо 2 • (–7) – 9 • (–3) = –14 + 27 = 13
Завдання 1061
Відомо, що пара чисел (–5;у) є розв’язком рівняння 2х + 9y=17. Знайдіть значення у.
Якщо x = –5, то 2 • (–5) + 9у = 17; –10 + 9у = 17; 9у = 27; у = 3
Завдання 1062
Відомо, що пара чисел (8;у) є розв’язком рівняння 2х – 3y = 4. Знайдіть значення у.
Якщо х = 8, то 2 • (–8) – 3у = 4; –16 – 3у = 4; –3у = 20; у=–20/3 =–6 2/3
Завдання 1063
Відомо, що пара чисел (x;2/3) є розв’язком рівняння 1/7х+ 6у = 1. Знайдіть значення х.
Якщо у = 2/3, то 1/7х + 6 • 2/3 = 1; 1/7х = 1 – 4; 1/7х = –3; х = –21
Завдання 1064
Відомо, що пара чисел (х;6) є розв’язком рівняння 8х – 3у = 22. Знайдіть значення х.
Якщо у = 6, то 8x – 3 • 6 = 22; 8x – 18 = 22; 8x = 40; x = 5
Завдання 1065
Графіку якого з рівнянь належить точка М(1;4):
1) 4y – 2х = –4; Не належить графіку, бо 4 • 4 – 2 • 1=16 – 2=14
2) 6х + 11y = 50. Належить графіку, бо 6 • 1 + 11 • 4=6 + 44=50
Завдання 1066
Чи проходить графік рівняння 3х + у = –1 через точку:
1) М(–3;10); Не проходить, бо 3 • (–3) + 10 = – 9 + 10 = 1
2) N(4;–13); Проходить, бо З • 4 + (–13) = 12 – 13 = –1
3) K(0;–1). Проходить, бо 3 • 0 + (–1) = 0 – 1 = –1
Завдання 1067
Виразіть із даного рівняння змінну х через змінну у і знайдіть які–небудь три розв’язки цього рівняння:
|
1) x + у = 12 х = 12 – у Якщо у = 12, то х = 12 – 12 = 0. Якщо у = 10, то х = 12 – 10 = 2 Якщо у = 1, то х = 12 – 1 = 11 (0;12), (2;10), (11;1) |
4) 2х + 8у = 16 2х = 16 – 8у х = 8 – у Якщо у = 0, то х = 8 – 0 = 8 Якщо у = 1, то х = 8 – 1 = 7 Якщо у = –1, то х = 8 + 1 = 9 (8;0), (7;1), (9;–1) |
|
2) х – 7у = 5 х = 5 + 7у Якщо у = 0, то х = 5 + 0 = 5 Якщо у = 1, то х = 5 + 7 = 12 Якщо у = –1, то х = 5 – 7 = – 2 (5;0), (12;1), (–2;–1)
|
5) –6х + 5у = 18 –6х = 8 – 5у х = –8/6 – 5/6у Якщо у = 0, то х = –8/6 – 0 = –8/6 Якщо у = 1, то х = –8/6 – 5/6 =–13/6=–2 1/6 Якщо у = –1, то х = –8/6 + 5/6 = –3/6=–1/2 (–8/6;0), (–2 1/6;1), (–1/2; –1) |
|
3) х + 6у = 10 х = 10 – 6у Якщо у = 0, то х = 10 – 0 = 10 Якщо у = 1, то х = 10 – 6 = 4 Якщо у = –1, то х = 10 + 6 = 16 (100), (4;1), (16;–1) |
5) 3х + 7у = 1 3х = 1 – 7у х = 1/3 – 7/3у Якщо у = 0, то х = 1/3 – 0 = 1/3 Якщо у = 1, то х = 1/3 – 7/3 = –6/3 = –2 Якщо у = –1, то х = 1/3 + 7/3 = 8/3 = 2 2/3 (1/3;0), (–2;1), (2 2/3;–1) |
Завдання 1068
Виразіть із даного рівняння змінну у через змінну х і знайдіть які–небудь два розв’язки цього рівняння:
|
1) 4х – у = 7 у = 4х – 7 Якщо х = 0, то у = 0 – 7 =–7 Якщо х = 1, то у = 4 – 7 =–3 (0;–7), (1;–3) |
2) –2х + у= 11 у = 2х + 11 Якщо х = 0, то у = 0 + 11 = 11 Якщо х = 1, то у = 2 + 11 = 13 (0; 11), (1; 13) |
|
3) 5х – Зу = 15 Якщо х = 0, то 5 • 0 – 3у = 15; –3у = 15; у = –5 Якщо х = 3, то 5 • 3 – 3у = 15; –3у = 0; у = 0 (0;–5), (3;0) |
|
Завдання 1069
Знайдіть які–небудь три розв’язки рівняння:
1) х – у = 10
Якщо х = 0, то 0 – у = 10; у = –10
Якщо х = 5, то 5 – у = 10; у = –5
Якщо х = 10, то 10 – у = 10; у = 0.
Відповідь: (0;–10), (5;–5), (10;0).
2) 2у – 5х = 11
Якщо х = 0, то 2у – 0 = 11; у = 5,5
Якщо х = 1, то 2у – 5 = 11; 2у = 16; у = 8
Якщо х = –1, то 2у + 5 = 11; 2у = 6; у = 3.
Відповідь: (0;5,5), (1;8), (–1;3).
Завдання 1070
Знайдіть які–небудь три розв’язки рівняння:
1) 6х + у = 7
Якщо х = 0, то 0 + у = 7; у = 7
Якщо х = 1, то 6 + у = 7; у = 1
Якщо х = 2, то 12 + у = 7; у = –5
Відповідь: (0;7), (1;1), (2;–5).
2) 2х – Зу = –4
Якщо х = 1, то 2 – Зу = –4; –Зу = –6; у = 2
Якщо х = 4, то 8 – Зу = –4; –Зу = –12; у = 4
Якщо х = –2, то –4 – Зу = –4; –Зу = 0; у = 0
Відповідь: (1;2), (4;4), (–2;0).
Завдання 1071 Побудуйте графік рівняння
|
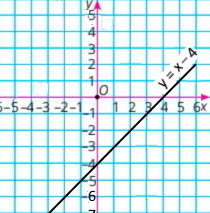
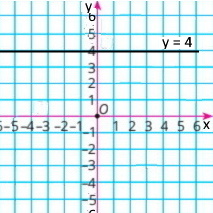
1) х – y = 4
|
3) х – 5y = 5
|
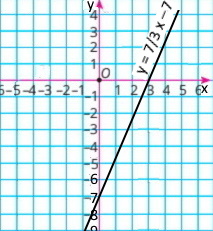
5)7х – 3y = 21
|
||||||||||||||||||
|
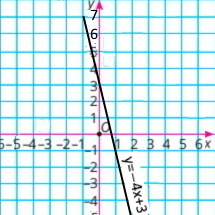
2) 4х + y = 3
|
4) 3х + 2y = 6
|
6) 0,2x + 2/3 y = 1
|
Завдання 1072
|
1) х + y = –3
|
2) 6х + y = 0
|
3) 2х – 3y = 9
|
Завдання 1073
Які пари чисел є розв’язками рівняння:
1) 0х + 4у = 20; 4у = 20; Рівняння набуває вигляду у = 5.
Розв’язком є пари чисел (х;5), де х — будь–яке число;
2) –Зх + 0у = 27; –Зх = 27; рівняння набуває вигляду х = –9.
Розв’язками є пари чисел (–9;у), де у — будь–яке число.
Завдання 1074
|
1) 4y = –8
|
2) 1,2х = 3,6
|
Завдання 1075
|
1) –0,2х = 1
|
2) 0,5у = 2
|
Завдання 1076
У якій точці пряма 7y – 3х = 21 перетинає:
1) вісь х; у = 0, то 0 – Зх = 21; х = –7, тому в точці (–7;0);
2) вісь у. х = 0, то 7у – 0 = 21; у = 3, тому в точці (0;3).
Завдання 1077
Знайдіть координати точок перетину прямої 0,Зх + 0,2y = 6 з осями координат.
у = 0, то 0,3х + 0 = 6; 0,3х = 6; х = 20, пряма перетинає вісь х у точці (20;0).
х = 0, то 0 + 0,2у = 6; 0,2у = 6; у = 30, пряма перетинає вісь у в точці (0;30).
Завдання 1078
Складіть лінійне рівняння з двома змінними, розв’язком якого є пара чисел (–2;1).
0,3х + у = 0,4
Завдання 1079
Складіть лінійне рівняння з двома змінними, розв’язком якого є пара чисел (3;5).
Зх + у = 14
Завдання 1080
Знайдіть розв’язок рівняння 7х + 8у = 30, який складається з двох рівних чисел.
Якщо х = у, то 7х + 8х = 30; 15х = 30; х = 2, розв'язком є пара чисел (2;2).
Завдання 1081
Знайдіть розв’язок рівняння –12х + 17у = –87, який складається з двох протилежних чисел.
Якщо х = –у, то –12(–у) + 17у = –87; 29у = –87; у = –3, розв’язком є пара чисел (3;–3).
Завдання 1082
При якому значенні а пара чисел (а;2а) є розв’язком рівняння 2х + 7у = 16?
2а + 7 • 2а = 16; 2а + 14а = 16; 16а = 16; а = 1, отже, при а = 1 розв'язок (1;2).
Завдання 1083
При якому значенні а пара чисел (–4;2) є розв’язком рівняння:
|
1) 3х + 5у = а 3 • (–4) + 5 • 2 = а –12 + 10 = а а = –2 |
2) ах + 5у = 18 –4а + 5 • 2 = 18 –4а = 8 а = –2 |
Завдання 1084
При якому значенні а графік рівняння 11х – 13у = а + 4 проходить через початок координат? Якщо х = у = 0, то 0 – 0 = а + 4; 0 = а + 4; а = –4
Завдання 1085
1) Графік рівняння 4х – 9у = а проходить через точку A(5;–3), якщо:
4 • 5 – 9 • (–3) = а; 20 + 27 = а; а = 47
2) графік рівняння 6х – ау = 15 проходить через точку А(5;–3), якщо:
6 • 5 – а • (–3) = 15; 30 + За = 15; 3a = –15; а = –5
Завдання 1086
При якому значенні а графік рівняння ах + 4у = 0 проходить через точку:
1) А(12;–4); а • 12 + 4 • (–4) = 0; 12а – 16 = 0; 12а = 16; а = 4/3 = 1 1/3;
2) В(0;2); а • 0 + 4 • 2 = 0; 0а = –8, розв'язків немає; не проходить через цю точку;
3) 0(0;0)? а • 0 + 4 • 0 = 0; 0а = 0, а — будь–яке число.
Завдання 1087
При якому значенні b графік рівняння 5х + by = 0 проходить через точку:
1) М(–4;–10); 5 • (–4) + b • (–10) = 0; –10b = 20; b = –2
2) N(0;1); 5 • 0 + b • 1 = 0; b = 0
3) К(–2;0)? 5 • (–2) + b • 0 = 0; 0b = 10, розв'язків немає; не проходить через цю точку.
Завдання 1088
Графіком яких із даних рівнянь є та сама пряма, що й графік рівняння 2х – 5у = 3:
1) 4х – 10y = 6; Почленно поділимо на 2, отримаємо рівняння 2х – 5y = 3
4) 5y – 2х = –3; Перенесемо доданки, отримаємо рівняння 2х – 5y = 3
5) х – 2,5у = 1,5; Почленно помножимо на 2, отримаємо рівняння 2х – 5y = 3
Завдання 1089
Складіть рівняння з двома змінними за такою умовою:
1) довжина прямокутника дорівнює х м, ширина — у м, периметр — 18 м; 2х + 2у = 18
2) автобус їхав 4 год зі швидкістю х км/год і 3 год зі швидкістю у км/год, проїхавши всього 250 км; 4х + Зу = 250
3) зошит коштує х грн, а ручка — у грн, 2 ручки дорожчі за 5 зошитів на 18 грн;
2у – 5х = 1,2
4) кусок сплаву масою х кг, який містив 12 % міді, та кусок сплаву масою у кг, який містив 20% міді, сплавили разом і отримали новий сплав, що містить 9 кг міді; 0,12х + 0,2у = 9
5) в одному ящику було х кг цукерок, а в другому — у кг; після того як із першого ящика переклали в другий 8 кг цукерок, в обох ящиках цукерок стало порівну. х – 8 = у + 8
Завдання 1090
Складіть рівняння з двома змінними за такою умовою:
1) бічна сторона рівнобедреного трикутника дорівнює а см, основа — b см, периметр — 32 см; 2а + b = 32
2) один автомобіль проїхав зі швидкістю х км/год за 6 год на 32 км менше, ніж другий автомобіль зі швидкістю у км/год за 7 год; 7у – 6х = 32
3) в одному магазині було х ц яблук, а в другому — у ц; за день у першому магазині продали 14 % яблук, а в другому — 18 % яблук, причому в другому магазині продали на 1,2 ц яблук менше, ніж у першому. 0,14х – 0,18у = 1,2
Завдання 1091
Доведіть, що прямі 5у – х = 6 і 3х – 7у = 6 перетинаються в точці А(9;3).
5 • 3 – 9 = 6 — пряма 5у – х = 6 проходить через точку A(9;3).
З • 9 – 7 • 3 = 27 – 21 = 6 — пряма Зх – 7у = 6 проходить через точку A(9;3).
Точка A(9;3) належить і прямій 5у – х = 6, і прямій Зх – 7у = 6, тому є спільною точкою для цих двох прямих, отже, прямі перетинаються в цій точці.
Завдання 1092
Доведіть, що прямі 4х – 3у = 12 і 3х + 4у = –66 перетинаються в точці В(–6;–12).
4 • (–6) – 3 • (–12) = –24 + 36 = 12 — пряма 4х – 3у = 12 проходить через точку B(–6;–12)
3 • (–6) + 4 • (–12) = –18 – 48 =–66 — пряма Зх + 4у=–66 проходить через точку В(–6;–12)
Точка B(–6;–12) належить і прямій 4х – Зу = 12, і прямій Зх + 4у = –66, тому є спільною точкою для цих двох прямих, отже, прямі перетинаються в цій точці.
Завдання 1093
Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точку:
1) А(2;8);
Графік проходить через початок координат, тому рівняння прямої у = kх.
Точка А(2;8) лежить на прямій, тому 8 = 2k; k = 4, отже, у = 4х або 4х – у = 0
2) В(–6;15).
Графік проходить через початок координат, тому рівняння прямої у = kх.
Точка В(–6;15) лежить на прямій, тому 15 = –6k; k = –2,5, отже, у = –2,5х або 2,5х + у = 0
Завдання 1094
Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точку С(8;–12).
Графік проходить через початок координат, тому рівняння прямої у = kх.
Точка С(8;–12) лежить на прямій, тому –12 = 8k; k = –1,5, отже, у = –1,5х або 1,5х + у = 0
Завдання 1095
Доведіть, що не існує такого значення а, при якому пряма ах – 3у = 12 проходить через початок координат.
Якщо пряма проходить через початок координат, тоді точка (0;0) лежить на прямій і
а • 0 – 3 • 0 = 0, а 0 ≠ 12. Отже, пряма не проходить через початок координат, тобто не існує такого значення а.
Завдання 1096
При яких значеннях a і b пряма ах + by = 24 перетинає осі координат у точках А(–6;0) і В(0;12)?
Точка А(–6:0) належить графіку
а • (–6) + 0 = 24
–6а = 24
а = –4
–4х + bу = 24
Точка В(0:12) належить графіку:
а • 0 + b • 12 = 24
b = 2
Відповідь: при а = –4 і b = 2.
Завдання 1097
На якому з рисунків 62, а–г зображено графік рівняння х + у = З?
Якщо у = 0, то х + 0 = 3; х = 3. Якщо х = 0, то 0 + у = 3; у = 3.
Отже, графік рівняння проходить через точки (3;0) і (0;3) і зображений на рисунку в).
Завдання 1098
На якому з рисунків 63, а–г зображено графік рівняння х – у = –5?
Якщо у = 0, то х – 0 = –5; х = –5. Якщо х = 0, то 0 – у = –5; у = 5.
Отже, графік рівняння проходить через точки (–5;0) і (0;5) і зображений на рисунку в).
Завдання 1099
Яка з прямих, зображених на рисунку 64, є графіком рівняння:
1) 0х + у = –3; у = –3, х – будь–яке число. Графіком є пряма d
2) 2х – у = 1; у = 2х – 1 Графіком є пряма с
3) 3х + 0у = 6; х = 2, у – будь–яке число. Графіком є пряма b
4) х + 2у = 0? 2у = –х, у = –0,5х Графіком є пряма а.
Завдання 1100
При якому значенні а точка перетину прямих 2х – 3у = –6 і 4х + у = а належить осі абсцис?
Якщо у = 0, то 2х – 0 = –6; х = –3. Пряма 2х – Зу = –6 перетинає вісь х в точці (–3;0).
Пряма 4х + у = а повинна перетинати вісь х у точці (–3;0). 4 • (–3) + 0 = а, тому а = –12
Завдання 1101
При якому значенні b точка перетину прямих 9х + 7у = 35 і х + bу = –20 належить осі ординат?
Якщо х = 0, то 0 + 7у = 35; у = 5. Пряма 9х + 7у = 35 перетинає вісь у в точці (0;5).
Пряма х + bу = –20 повинна перетинати вісь у в точці (0;5). 0 + b • 5 = –20; тому b = –4
Завдання 1102
Чи належить графіку рівняння 13х + 17y = –40 хоча б одна точка, обидві координати якої — додатні числа? Якщо обидві координати точки додатні, то сума додатніх чисел не може бути від'ємною, тому графіку не належить жодна така точка.
Завдання 1103
Чи належить графіку рівняння 4х – 8у = 7 хоча б одна точка, обидві координати якої — цілі числа?
8у = 4х – 7; у = 1/2 х – 7/8, обидві координати не можуть бути цілими числами, тому графіку не належить жодна така точка.
Завдання 1104
Складіть лінійне рівняння з двома змінними, графік якого перетинає осі координат у точках:
1) А(–4;0) і В(0;2);
Графік перетинає осі координат, тому рівняння прямої у = kх + b.
Точка В(0;2) лежить на прямій, тому 2 = 0k + b; b = 2, отже, у = kх + 2.
Точка A(–4;0) лежить на прямій, тому 0 = –4k + 2; 4k = 2; k = 0,5
Рівняння має вигляд 0,5х – у = –2
2) 0(0;–3) і В(5;0).
Графік перетинає осі координат, тому рівняння прямої у = kх + b.
Точку С(0;–3) лежить на прямій, тому –3 = 0k + b; b = –3, отже, у = kх – 3.
Точка D(5;0) лежить на прямій, тому 0 = 5k – 3; 5k = 3; k = 0,6
Рівняння має вигляд: 0,6х – у = 3
Завдання 1105
Складіть лінійне рівняння з двома змінними, графік якого проходить через точки М(6;0) і K(0;6).
Графік перетинає осі координат, тому рівняння прямої у = kх + b.
Точка K(0;6) лежить на прямій, тому 6 = 0k + b; b = 6, отже, у = kх + 6
Точка М(6;0) лежить на прямій, тому 0 = 6k + 6; 6k = –6; k = –1
Рівняння має вигляд х + у = 6
Завдання 1106
Складіть рівняння, графіки яких зображено на рисунку 65.
Прямі а і с перетинають осі координат, тому рівняння прямої у = kх + b
Точка (0;3) лежить на прямій а, тому З = k • 0 + b; b = 3, отже, у = kх + 3
Точка (–1;0) лежить на прямій а, тому 0 = k • (–1) + 3; k = 3, отже, у = 3х + 3
Рівняння прямої а буде мати вигляд: –3х – у = 3
Точка (0;–2) лежить на прямій с, тому –2 = k • 0 + b; b = –2, отже, у = kх – 2
Точка (4;0) лежить на прямій с, тому 0 = 4k – 2; 4k = 2, k = 0,5, отже, у = 0,5х – 2
Рівняння прямої с буде мати вигляд: 0,5х – у = 2
Пряма d проходить через початок координат, тому рівняння прямої у = kх
Точка (–2;2) лежить на прямій d, тому –2 = 2k, k = –1, отже у = –х
Рівняння прямої d буде мати вигляд: х + у = 0
Пряма m паралельна осі ординат і проходить через точку (–2;2).
Рівняння прямої m буде мати вигляд: х= –2
Завдання 1107
Складіть рівняння, графіки яких зображено на рисунку 66.
Прямі m і n перетинають осі координат, тому рівняння прямої у = kх + b
Точка (0;–3) лежить на прямій m, тому –З = k • 0 + b; b = –3, отже, у = kх – 3
Точка (1;0) лежить на прямій m, тому 0 = k – 3; k = 3, отже, у = 3х – 3
Рівняння прямої m буде мати вигляд: 3х – у = 3
Точка (0;2) лежить на прямій n, тому 2 = k • 0 + b; b = 2, отже, у = kх + 2
Точка (0;3) лежить на прямій n, тому 0 = 3k + 2; 3k = –2, k = –2/3, отже, у = –2/3 х + 2
Рівняння прямої с буде мати вигляд: 0,5х – у = 2
Пряма b паралельна осі абсцис і проходить через точку (3;0).
Рівняння прямої b буде мати вигляд: y = 3
Завдання 1108
Скільки існує пар простих чисел (х;у), які є розв’язками рівняння 5х – 6у = З?
5х – 6у = 3; 5х = 6у + 3; 5x = 3(2у + 1). З останньої рівності слідує, що число х ділиться
на 3. Єдиним простим числом, яке ділиться на 3 є саме число 3.
Якщо х = 3, то 5 • 3 – 6у = 3; –6у = –12; у = 2. Отже, існує одна пара простих чисел
(3;2), яка є розв’язком рівняння 5х – 6у = 3.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 1109
Петру Івановичу треба купити 2 буханці хліба, 800 г ковбаси та 0,5 кг шинки. У таблиці наведено ціни на ці продукти в трьох магазинах, найближчих до дому Петра Івановича.
|
Магазин |
Ціна, грн |
||
|
|
Хліб (за буханець) |
Ковбаса (за 1 кг) |
Шинка (за 1 кг) |
|
«Смачно» |
26 |
280 | 400 |
|
«Апетит» |
24 | 270 | 360 |
|
«Свіжі продукти» |
28 | 310 | 480 |
У магазині «Смачно» у Петра Івановича є дисконтна картка зі знижкою в розмірі 5 % на всі продукти. У магазині «Свіжі продукти» цього дня діє знижка в розмірі 10 % на всі ковбасні та м’ясні вироби. У якому магазині Петру Івановичу найвигідніше зробити покупку?
Розв'язання
26 • 2 + 280 • 0,8 + 400 • 0,5 = 52 + 224 + 200 = 476 (грн) – вартість продуктів в «Смачно»;
476 • 0,95 = 452,2 (грн) – вартість зі знижкою продуктів в «Смачно»;
24 • 2 + 270 • 0,8 + 360 • 0,5 = 48 + 216 + 180 = 444 (грн)– вартість продуктів в «Апетит»:
28 • 2 + 310 • 0,8 • 0,9 + 480 • 0,5 • 0,9 = 56 + 223,2 + 216 = 495,2 (грн) – вартість продуктів в «Апетит».
Відповідь: найдешевше буде в магазині «Апетит», де нема знижок, 444 грн.
Завдання 1110
Дві бригади виготовили 840 деталей, причому одна бригада виготовила на 80 % більше деталей, ніж друга. Скільки деталей виготовила кожна бригада?
Розв'язання
Нехай друга бригада виготовила х деталей, тоді перша бригада — 1,8х деталей. Складаємо рівняння:
1,8х + х = 840
2,8х = 840
х = 300 (д.) – виготовила деталей друга бригада;
1,8 • 300 = 540 (д.) – виготовила друга бригада.
Відповідь: 540 деталей, 300 деталей.
Завдання 1111
Відомо, що 4 однакових екскаватори можуть вирити котлован за 12 год. За який час 6 таких самих екскаваторів вириють 3 таких котловани?
Розв'язання
1) 12 • 4 = 48 (год) — потрібно одному екскаватору, щоб вирити один котлован;
2) 48 : 6 = 8 (год) — потрібно шести екскаваторам, щоб вирити один котлован;
3) 8 • 3 = 24 (год) — потрібно шести екскаваторам, щоб вирити три котловани.
Відповідь: За 24 год.
Завдання 1112
Доведіть, що значення виразу 236 + 4100 – 232 – 498 кратне числу:
1) 15;
236 + 4100 – 232 – 498 = 236 – 232 + 4100 – 498 =
= 232 • (24 – 1) + 498 • (4² – 1) = 232 • (16 – 1) + 498 • (16 – 1) =
= 15 • (232 + 498) — кратне числу 15;
2) 240.
236 + 4100 – 232 – 498 = 236 – 232 + 41100 – 498 = 232 • (24 – 1) + 498 • (42 – 1) =
= 232 • (16 – 1) + 498 • (16 – 1) = 15 • (232 + 498) = 15 • (16 • 228 + 16 • 496) =
= 15 • 16 • (228 + 496) = 240 • (228 + 496) — кратне числу 240.
Завдання 1113 Рівняння
|
1) (х – 8)² – (х – 4)(х + 4) = 0 x² – 16х + 64 – х² + 16 = 0 х = 5 |
2) (4х – 5)(4х + 5) – (4х – 1)² = 9 – 2х х = 3,5 |
Завдання 1114 Розклад на множники
1) 6х3 – 8x2 + Зху – 4у = 2х2(3х – 4) + у(3х – 4) = (Зх – 4)(2х2 + у)
2) х4 – 6х2у + 9y2 – 16 = (х2 – Зу)2 – 16 = (х2 – Зу – 4)(х2 – Зу + 4)
3) (125x3)/27 – (m6n9)/64 =
= (5x/3)3 – ((m2n3)/4)3=(5x/3 – (m2n3)/4)((25x2)/9 + 5x/3 • (m2n3)/4 + (m4n6)/16) =
= (5x/3 – (m2n3)/4)((25x2)/9 + (5xm2n3)/12 + (m4n6)/16)
4) с² – 2с – b² – 4b – 3 = с² – 2с + 1 – (b² + 4b + 4) = (с – 1)² – (b + 2)² =
= (с – 1 – b – 2)(с – 1 + b + 2) = (с – b – 3)(с + b + 1)
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
Завдання 1115
Яка з пар чисел (3;3), (–3;3), (–3;–3) є розв’язком кожного з рівнянь х² + у²=18 і х + у = 0?
Розв’язком кожного з рівнянь х² + у² = 18 і х + у = 0 є пара чисел (–3; 3), бо
(–3)² + З² = 9 + 9 = 18 і –3 + 3 = 0
Завдання 1116
На рисунку 67 зображено графіки рівнянь у = х² і х – у + 2 = 0. Користуючись цим рисунком, знайдіть усі пари чисел, які є розв’язками кожного з даних рівнянь.
Розв’язками кожного з рівнянь у = х² і х – у + 2 = 0 є пари чисел (–1;1) і (2;4).
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
Завдання 1117
Сума 100 різних натуральних чисел дорівнює 5051. Знайдіть ці числа.
Знайдемо суму 100 найменших різних натуральних чисел:
1 + 2 + 3 + 4 + ... + 97 + 98 + 99 + 100 =
= (1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) +... + (50 + 51) = 101 • 50 = 5050.
Суму 5051 можна отримати із тих же доданків замінивши доданок 100 на 101.