Інші завдання дивись тут...

Завдання 1118

Яка з пар чисел (–2;1), (2;–1), (6;4), (8;–4) є розв’язком системи рівнянь

(–2;1)	(2;–1)	(6;4)	(8;–4)
{3х – 8y = –14   4х + у = 28 3 • (–2) – 8 • 1=–14 4 • (–2) + 4 = –4 Не є розв'язком	{3х – 8y = –14   4х + у = 28 3 • 2 – 8 • (–1)=14 Не є розв'язком	{3х – 8y = –14   4х + у = 28 3 • 6 – 8 • 4=–14 4 • 6 + 4 = 28 Є розв'язком	{3х – 8y = –14   4х + у = 28 3 • 8 – 8 • (–4)=64 Не є розв'язком

Завдання 1119 

Чи є правильним твердження:

1) Так	2) Ні	3) Так	4) Ні	5) Так
{у – х = 5 3х + 2у = 4 пара (0;0) 0 – 0 = 0 не є розв'язком	{х + у = 1 3х + 2у = –1 пара (–1;2) –1 + 2 = 1 3 • (–1) + 2 • 2=1 не є розв'язком	{2у – х = –4 3х + 2у = 1 пара (2:–1) 2 • 2 – (–1)=5 не є розв'язком	{х + у = 8 х – у = 9 пара (9:–1) 9 + (–1) = 8 9 – (–1) = 10 не є розв'язком	{4х + 5у = 6 5у + 4х = 7 не  має розв'язків, вираз набуває різних значень

Завдання 1120

Розв’язком яких систем рівнянь є пара чисел (–5;2):

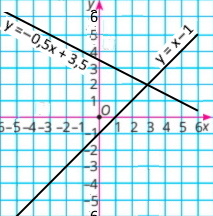
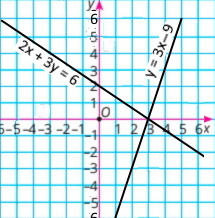
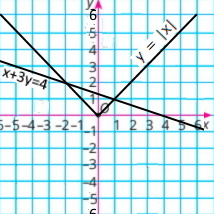
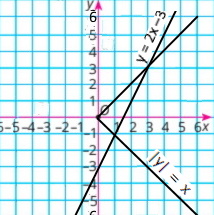
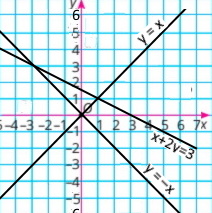
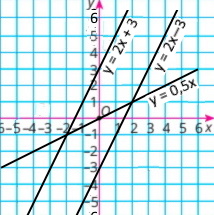
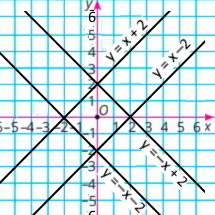
Визначте координати точки перетину прямих, зображених на рисунку 70. Запишіть відповідну систему рівнянь, перевірте знайдений розв’язок системи, підставивши координати точки перетину прямих у рівняння системи.

а) координати точки (1;4) є розв’язком системи {x + y = 5  3x + y = 7, бо 1 + 4 = 5, 3 • 1 + 4 = 7

б) координати точки (–1;–1) є розв’язком системи {y + 2x = –3  –2x + y = 1, бо –1 + 2 • (–1) = –3, –2 • (–1) + (–1) = 1

Завдання 1122

Розв’яжіть графічно систему рівнянь:

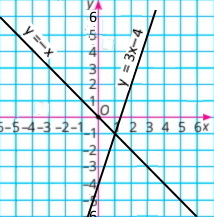
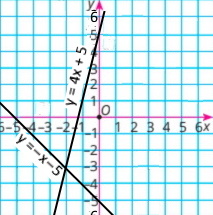
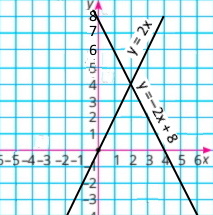
1) х – у = 1    х + 2у = 7		3) х + у = –5    4х – у = –5		5) 2х + у = 8    2х – у = 0
у=х–1 х 0 4 у –1 3	у=–0,5х+3,5 х –5 7 у 6 0	у=–х–5 х 0 1 у –5 –6	у=4х+5 х 0 1 у 5 9	у=–2х+8 х 0 1 у 8 6	у=2х х –1 1 у –2 2
Розв'язок (3;2)		Розв'язок (–2;–3)		Розв'язок (2;4)
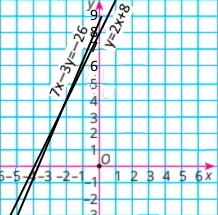
2) х + у = 0    3х – у = 4		4) 2x + 3y = 6     3х – у = 9		6) 7х – 3у = –26     у – 2х = 8
у=–х х –1 0 у 1 0	у=3х–4 х 0 1 у –4 –1	у=–2/3х+2 х 0 3 у 2 0	у=3х–9 х 0 3 у –9 0	у=7/3х+26/3 х –2 –5 у 4 –3	у=2х+8 х –4 0 у 0 8
Розв'язок (1;–1)		Розв'язок (3;0)		Розв'язок (–2;4)

Завдання 1123

Розв'яжіть графічно систему рівнянь:

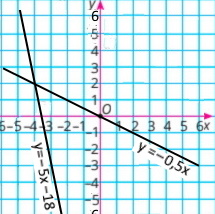
1) {х + 2у = 0      5х + у = –18		3) {х – 2у = 1      y – x = –2
у = –0,5x х –2 2 у 1 –1	y = –5х – 18 х –3 –4 у –3 2	y = 0,5x – 0,5 х –5 5 у –3 2	y = х – 2 х 0 3 у –2 1
Розв'язок (–4;2)		Розв'язок (3;1)
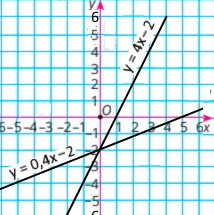
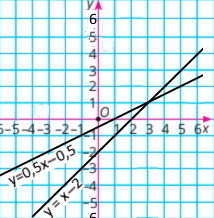
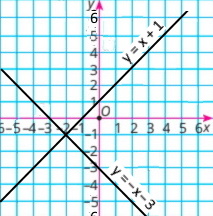
2) {2x – 5y = 10      4х – у = 2		4) {х + у = –3      х – у = –1
y = 0,4х – 2 х –5 5 у –4 0	y = 4х – 2 х 0 1 у –2 2	у = –x – 3 х 0 2 у –3 –5	у = x + 1 х 0 2 у 1 3
Розв'язок (0;–2)		Розв'язок (–2;–1)

Завдання 1124

Складіть яку–небудь систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара значень змінних:

1) х = 3, у = 2;

Підставимо (3;2) у формулу y = kx + b, отримаємо: 2 = 3k + b

Якщо k = 1, то 2 = 3 + b; b = –1, рівняння має вигляд: у = х – 1

Якщо k = 2, то 2 = 6 + b; b = –4, рівняння має вигляд: у = 2х – 4

Маємо систему двох лінійних рівнянь з двома змінними:

{x – y = 1

 2x – y = 4

2) х = –4, у = 1;

Підставимо (–4;1) у формулу y = kx + b, отримаємо: 1 = –4k + b

Якщо k = 1, то 1 = –4 + b; b = 5, рівняння має вигляд: у = х + 5

Якщо k = 2, то 1 = –8 + b; b = 9, рівняння має вигляд: у = 2х + 9

Маємо систему двох лінійних рівнянь з двома змінними:

{x – y = –5

 2x – y = –9

3) х = 5, у = 0.

Підставимо (5;0) у формулу y = kx + b, отримаємо: 0 = 5k + b

Якщо k = 1, то 0 = 5 + b; b = –5, рівняння має вигляд: у = х – 5

Якщо k = 2, то 0 = 10 + b; b = –10, рівняння має вигляд: у = 2х – 10

Маємо систему двох лінійних рівнянь з двома змінними:

{x – y = 5

 2x – y = 10

 

Завдання 1125

Складіть яку–небудь систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел (2;–2).

Підставимо (2;–2) у формулу y = kx + b, отримаємо: –2 = 2k + b

Якщо k = 1, то –2 = 2 + b; b = –4, рівняння має вигляд: у = х – 4

Якщо k = 2, то –2 = 4 + b; b = –6, рівняння має вигляд: у = 2х – 6

Маємо систему двох лінійних рівнянь з двома змінними:

{x – y = 4

 2x – y = 6

 

Завдання 1126

Знайдіть значення а і b, якщо пара (6;4) є розв’язком системи рівнянь:

1) {ах + 2у = 26      4х + bу = 14	2) {5х + bу = 6     ах + bу = 0
{а • 6 + 2 • 4 = 26     4 • 6 + b • 4 = 14    {6a = 18     4b = –10    {a = 3     b = –2,5	{5 • 6 + b • 4 = 6     а • 6 + b • 4 = 0    {4b = –24     6a + 4b = 0    {b = –6      a = 4

Завдання 1127

При яких значеннях а і b пара чисел (–2;3) є розв’язком системи рівнянь:

{ах – 3у = –13

 7х + bу = 1

{a • (–2) – 3 • 3 = –13

 7 • (–2) + b • 3 = 1

{–2a = –4

 3b = 15

{a = 2

 b = 5

 

Завдання 1128

Чи має розв’язок система рівнянь:

1) {2х – 7у = 6    |•4      8x – 28y = 24    {8x – 28y = 24      8x – 28y = 24 Має безліч розв’язків, бо вираз одночасно набуває однакових значень

2) {2х + у = –2   |•3      6x + 3y = 9    {6x + 3y = –6      6x + 3y = 9 Не має розв’язків, бо вираз одночасно набуває різних значень

3) {x + 2y = 0,5   |•2      2x + 4y = 2     {2x + 4y = 1      2x + 4y = 2 Не має розв’язків, бо вираз одночасно набуває різних значень

Завдання 1129

Чи має розв’язок система рівнянь:

1) {x – y = 4   |•3      3x – 3y = 6    {3x – 3y = 12      3x – 3y = 6 Не має розв’язків, бо вираз одночасно набуває різних значень

2) {x – 1,5y = –4  |•(–2)      3y – 2x = 8    {–2x + 3y = 8      –2x + 3y = 8 Має безліч розв'язків, бо вираз одночасно набуває однакових значень

3) {9x + 9y = 18   |:9      x + y = 2     {x + y = 2      x + y = 2 Має безліч розв'язків, бо вираз одночасно набуває однакових значень

Завдання 1130

До рівняння 2х – 3у = 6 доберіть друге лінійне рівняння таке, щоб отримати систему рівнянь, яка:

1) має єдиний розв’язок	2) має безліч розв’язків;	3) не має розв’язків
3x – y = 5 Прямі перетинаються	4х – 6у = 12 Прямі збігаються	2х – 3у = 5 Прямі паралельні

Завдання 1131

До рівняння х – у = 2 доберіть друге лінійне рівняння таке, щоб отримати систему рівнянь, яка:

1) має єдиний розв’язок	2) має безліч розв’язків;	3) не має розв’язків
2x – y = 5 Прямі перетинаються	2х – 2у = 4 Прямі збігаються	х – у = 3 Прямі паралельні

Завдання 1132

При яких значеннях а не має розв’язків система рівнянь

{8x + 9y = 7

 8х + 9у = а

Коли вираз одночасно набуває різних значень, тому при а ≠ 7.

 

Завдання 1133

При якому значенні а має безліч розв’язків система рівнянь:

1) {х + 5у = 4      |•4      4x + 20y = a     {4х + 20у = 16      4x + 20y = a Коли вираз одночасно набуває однакових значень, тому при a = 16

2) {3x + ay = 12      9x – 15y = 36    |:3     {3x + ay = 12      3x – 5y = 12 Коли вираз одночасно набуває однакових значень, тому при a = –5

Завдання 1134

При яких значеннях а система рівнянь:

1) не має розв язків;	2) має безліч розв’язків?
{7x – 12y = 14  7х – 12у = а  Коли вираз одночасно набуває  різних значень, тому при a ≠ 14	{6х + ay = 4  3х – 5у = 2   |•2 {6х + ay = 4  6х – 10у = 4 Коли вираз одночасно набуває однакових значень, тому при a = –10

Завдання 1135

Доберіть такі значення а і b, при яких система рівнянь

{х – 2у = З

 ах + 4у = b

{х – 2у = З    |•(–2)

 ах + 4у = b

{–2x + 4y = –6

 ах + 4у = b

1) має безліч розв’язків; 

Коли вираз одночасно набуває однакових значень, тому при a = –2 і b = –6

2) має єдиний розв’язок;

При a = 1 і b = 2

3) не має розв’язків.

Коли вираз одночасно набуває різних значень, тому при a = –2 і b ≠ –6

 

Завдання 1136

Доберіть такі значення m і n, при яких система рівнянь

{х + у = 5

 3х – mу = n

{х + у = 5      |•3

 3х – mу = n

{3x + 3y = 15

 3x – my = n

1) має безліч розв’язків;

Коли вираз одночасно набуває однакових значень, тому при m = –3, n = 15

2) має єдиний розв’язок; 

При m = 6, n = 2

3) не має розв’язків.

Коли вираз одночасно набуває різних значень, тому при m = –3, n ≠ 15

 

Завдання 1137

Розв'яжіть графічно систему рівнянь:

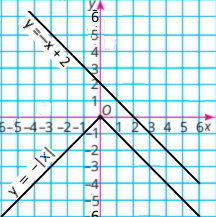
1) |x| – y = 0     x – y = –4		3) y + |x| = 0     x + y = 2
у = |x| у = х, якщо х ≥ 0 у = –х, якщо x < 0 х –2 0 2 у 2 0 2	y = х + 4 х 0 1 у 4 5	у = –|x| у = –х, якщо х ≥ 0 у = х, якщо x < 0 х –2 0 2 у –2 0 –2	y = –х + 2 х 0 3 у 2 –1
Розв'язок (–2;2)		Розв'язків немає
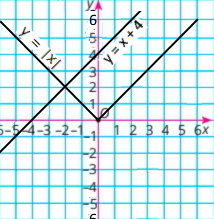
2) |x| – y = 0 x + 3y = 4		4) x – |y| = 0    2x – y = 3
у = |x| у = х, якщо х ≥ 0 у = –х, якщо x < 0 х –1 0 1 у 1 0 1	y = –1/3 х + 4/3 х –2 4 у 2 0	|у| = х у = х, якщо у ≥ 0 –у = х, якщо у < 0 х 1 0 1 у –1 0 1	у = 2x – 3 х 0 2 у –3 1
Розв'язки (–2;2) і (1;1)		Розв'язки (3;3) і (–1;1)

Завдання 1138

Розв’яжіть графічно систему рівнянь:

1) x² – y² = 0    х + 2у = 3			2) |y – 2x| = 3      х – 2у = 0
x² – y² = 0 (x – y)(х + у) = 0 х – у = 0 або х + у=0 у = х           у = –х		х + 2у = 3 2у = –х + 3 у =–0,5х + 1,5	|y – 2x| = 3 y – 2x =3 або y – 2x =–3 y = 2x + 3     у = 2х – 3		х – 2у=0 2у = х у = 0,5х
х –1 1 у –1 1	х –1 1 у 1 –1	х –5 5 у 4 –1	х 0 1 у 3 5	х 0 2 у –3 1	х –2 2 у –1 1
Два розв'язки (–3;2) і (1;1)			Два розв'язки (–2;–1) і (2;1)
3) х² – 2ху + у² = 4    |х + у| = 2
х² – 2ху + у² = 4 (х – у)² = 2²  |х – у| = 2 х – у = 2 або х – у = –2 у = х – 2 або у = х + 2			|х + у| = 2 х + у = 2 або х + у = –2 у = –х + 2 або у = –х –2
х 0 3 у –2 1		х 0 1 у 2 3	х 0 1 у 2 1		х 0 2 у –2 –4
Чотири розв'язки (2;0), (–2;0), (0;2) і (0;–2)

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

Завдання 1139

Математичний гурток відвідують 30 учениць 5–8 класів. На діаграмі (рис. 71) показано розподіл їх за класами.

Чи є правильним твердження:

1) шестикласниць більше, ніж семикласниць; Ні

2) восьмикласниць більше, ніж разом п’ятикласниць і шестикласниць; Твк

3) восьмикласниць менше, ніж семикласниць; Ні

4) семикласниці становлять понад 25 % членів гуртка; Так

5) восьмикласниці становлять понад 50 % членів гуртка; Ні

6) шестикласниць і семикласниць разом 15 осіб; Так

7) семикласниць і восьмикласниць разом менше, ніж 20 осіб? Ні

 

Завдання 1140

Зливок сплаву міді й олова масою 5,5 кг містить міді на 20 % більше, ніж олова. Знайдіть масу міді в цьому зливку.

Розв'язання

Нехай маса міді в зливку дорівнює x кг, тоді маса олова дорівнює (x – 0,2x) кг. Складаємо рівняння:

x + (x – 0,2x) = 5,5

x + x – 0,2x = 5,5

1,8x = 5,5

x = 3

Відповідь: 3 кг.

 

Завдання 1141

Із Києва до Лубен, відстань між якими дорівнює 200 км, виїхав автобус. Через 32 хв після виїзду автобуса назустріч йому з Лубен виїхав автомобіль зі швидкістю, на 20 км/год більшою за швидкість автобуса. З якою швидкістю рухався автобус, якщо вони зустрілися через 1,2 год після виїзду автомобіля?

Розв'язання 

Нехай швидкість автобуса дорівнює x км/год, тоді швидкість автомобіля дорівнює (x + 20) км/год. До зустрічі автобус проїхав (32/60 + 1,2)x = (8/15 + 1,2)х км, а автомобіль — 1,2(x + 20) км. Складаємо рівняння:

(8/15 + 1,2)x + 1,2(x + 20) = 200    |•15

(8 + 18)x + 18(x + 20) = 3000

26x + 18x + 360 = 3000

44x = 3640

x = 60 (км/год) – швидкість автобуса.

Відповідь 60 км/год.

 

Завдання 1142

Знайдіть чотири послідовних непарних натуральних числа, сума квадратів яких дорівнює 164.

Чотири послідовних непарних натуральних чисел можна записати так: 2n – 3; 2n – 1; 2n + 1; 2n + 3. Складаємо рівняння:

(2n – 3)² + (2n – 1)² + (2n + 1)² + (2n + 3)² = 164

4n² – 12n + 9 + 4n² – 4n + 1 + 4n² + 4n + 1 + 4n² + 12n + 9 = 164

16n² + 20 = 164

16n² = 144

n² = 9

n = 3

2n – 3 = 2 • 3 – 3 = 6 – 3 = 3 – перше число; 

2n – 1 = 2 • 3 – 1 = 6 – 1 = 5 – друге число;

2n + 1 = 2 • 3 + 1 = 6 + 1 = 7 – третє число;

2n + 3 = 2 • 3 + 3 = 6 + 3 = 9 – четверте число.

Відповідь: 3; 5; 7; 9.

 

Завдання 1143

Доведіть, що коли х + у = а – 1, то ах + х + ау + у + 1 = а².

ax + x + ay + y + 1 = x(a + 1) + y(a + 1) + 1 = (a + 1)(x + y) + 1

Якщо x + y = a – 1, тоді (a + 1)(x + y) + 1 = (a + 1)(a – 1) + 1 = a² – 1 + 1 = a²

 

Завдання 1144

Остача при діленні числа а на 5 дорівнює 4, а остача при діленні на 5 числа b дорівнює 3. Доведіть, що значення виразу а² + b² кратне 5.

Якщо остачі від ділення чисел a і b на 5 відповідно дорівнюють 3 і 4, то

a = 5n + 4 і b = 5m + 3.

Маємо: a² + b² =(5n + 4)² + (5m + 3)² = 25n² + 40n + 16 + 25m² + 30m + 9 =

= 25n² + 40n + 25m² + 30m + 25 = 5(5n² + 8n + 5m² + 6m + 5) – кратне 5.

 

ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ

Завдання 1145

Виразіть у через х і х через у у рівняннях:

1) x + y = 10    x = 10 – y    y = 10 – x	3) у – х = –4    x = y + 4    y = x – 4	5) 5у – 4х = 0    x = 5/4y    y = 4/5x
2) 2x + y = 7    x = (7 – y)/2    y = 7 – 2x	4) х – 6у = 1    x = 1 + 6y    y = (x – 1)/6	6) 4х + 3у = –12     x = (–12 – 3y)/4     y = (–12 – 4x)/3

УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ

Завдання 1146

Десятковий запис одного п’ятицифрового числа складається тільки із цифр 2 і 3, а другого п’ятицифрового числа — тільки із цифр 3 і 4. Чи може запис добутку цих чисел складатися тільки із цифр 2 і 4?

Розглянемо всі можливі останні цифри указаних чисел.

І	2	2	3	3
ІІ	3	4	3	4
Добуток	6	8	9	2

Отже, останньою цифрою першого числа може бути тільки цифра 3, а другого — тільки цифра 4, тоді остання цифра добутку дорівнює 2.

Розглянемо аналогічно для десятків.

І	23	23	33	33
ІІ	34	44	34	44
Добуток	82	12	22	52

Отже, можливий лише варіант, коли кількість десятків першого числа дорівнює 3 і другого — 3. Аналогічно кількість сотень чисел і далі може дорівнювати відповідно 3 і 3. Але тоді перша цифра добутку 33333 • 33334 дорівнює 1, що неможливо. Отже запис добутку заданих в умові задачі чисел не може складатися тільки з цифр 2 і 4.

Інші завдання дивись тут...