Завдання 984
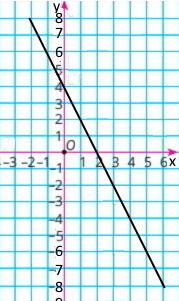
Формула функції прямої пропорційності, графік проходить через M(2;–5).
Рівняння прямої пропорційності у = kx.
Точка M(2;–5) лежить на прямій, тому –5 = 2k; k = –2,5, отже, формула у = –2,5х
Завдання 985
Значення b, при якому графік функції у = –1/9x + b проходить через A(–27;4).
Точка A(–27;4) належить графіку, тому 4 = –1/9 • (–27) + b; 4 = 3 + b; b = 4 – 3 = 1
Завдання 986
Значенні k при якому графік функції y = kx – 15 проходить через точку B(3;–6).
y = kx – 15; –6 = 3k – 15; 3k = 9; k = 3
Завдання 987
Графік функції y = kx + b перетинає осі координат у точках C(0;4) і D(–8;0). Знайдіть значення k і b.
Точка С(0;4) належить графіку, тому 4 = k • 0 + b; b = 4, отже, y = kx + 4
Точка D(–8;0) належить графіку, тому 0 = –8k + 4; 8k = 4, k = 0,5
Відповідь: k = 0,5; b = 4.
Завдання 988
Графік функції y = kx + b перетинає осі координат у точках M(3;0) і K(0;–1). Знайдіть значення k і b.
Точка К(0,–1) належить графіку, тому –1 = k • 0 + b; b = –1, отже, y = kx – 1
Точка М(3;0) належить графіку, тому 0 = 3k – 1; 3k = 1; k = 1/3
Відповідь: k = 1/3; b = –1.
Завдання 989
Усі точки графіка функції y = kx + b мають однакову ординату, яка дорівнює –6. Знайдіть значення k і b.
Якщо всі точки мають однакову ординату, то графік паралельний осі абсцис.
у = –6, то b = –6, тоді –6 = kx + 6; kx = 0, ле х – будь-яке, тому k = 0
Відповідь: k = 0 і b = –6.
Завдання 990
Графік функції y = kx + b паралельний осі абсцис і проходить через точку A(–2;3). Знайдіть значення k і b.
Якщо графік паралельний осі абсцис, всі точки мають однакову ординату.
Точка A(–2;3) належить графіку, то всі точки мають ординату 3, тому b = 3, у = kx + 3.
3 = –2k + 3$ –2k = 0; k = 0
Відповідь: k = 0, b = 3.
Завдання 991
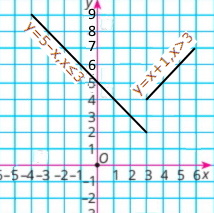
1) Графік, зображений на рис. 44:
а) відображає процес витікання води з бака,
б) відображає процес наповнювання водою бака;
2) Спочатку було в баках: а) 50 л води; б) 10 л води.
3) Через 2 хв після відкриття кранів у баках було: а) 40 л води; б) 15 л води;
через 6 хв після відкриття кранів у баках було: а) 20 л поди; б) 25 л води;
4) 30 л води після відкриття в баках було: а) через 4 хв; б) через 8 хв.
5) Щохвилини води у баках: а) наливається 10 : 4 = 2,5 л; б) виливається 10 : 2 = 5 л;
6) формули залежності кількості води в баках від часу, а) у = 50 – 5х; б): у = 10 + 2,5х.
Завдання 992
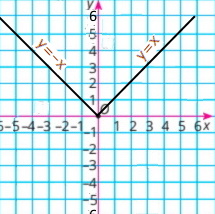
Яка з прямих, зображених на рисунку 45, є графіком функції:
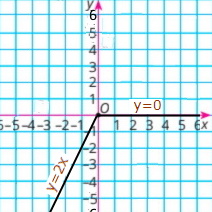
1) y = x; Пряма b, бо х = 1, то у = 1, точка (1;1);
2) y = 4x; Пряма а, бо х = 1, то у = 4, точка (1;4);
3) y = 1/4x; Пряма с, бо х = 1, то у = 1/4, точка (1;1/4);
4) y = –1/4x. Пряма d, бо х = 1, то у = –1/4 = –0,25, точка (1;–1/4).
Завдання 993
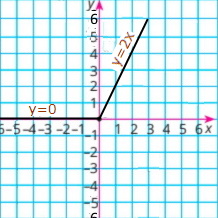
Яка з прямих, зображених на рисунку 46, є графіком функції:
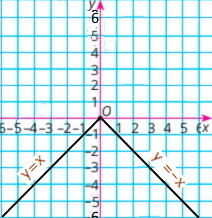
1) y = –x; Пряма n, бо х = 1, то у = –1, точка (1;–1);
2) у = 3x; Пряма k, бо х = 1, то у = 3, точка (1;3);
3) у = –1х; Пряма m, бо х = 1, то у = –1, точка (1;–1);
4) у = –2x? Пряма p, бо х = 1, то у = –2, точка (1;–2).
Завдання 994
Задайте формулою які–небудь дві лінійні функції, графіки яких проходять через точку:
|
1) A(0;4) |
2) B(1;3) |
|
у = аx + b 4 = а • 0 + b b = 4, а – будь–яке число Наприклад, а = 1, формула у = х + b а = 2, формула у = 2х + b |
у = аx + b 3 = а • 1 + b а + b = 3 Наприклад, а = 1, b = 2, формула у = х + 2 а = 2, b = 1, формула у = 2х + 1 |
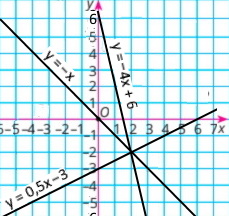
Завдання 995
Графіки функцій у = 0,5x – 3, у = –4x + 6 і у = kx перетинаються в одній точці. Знайдіть значення k. Побудуйте в одній системі координат графіки цих функцій.
0,5х – 3 = –4х + 6
0,5х + 4х = 6 + 3
4,5х = 9
х = 2
Якщо х = 2, то у = 0,5 • 2 – 3 = 1 – 3 = –2, координати точки (2;–2).
–2 = k • 2; k = –1, тому формула графіка функції у = –х
|
1) у = 0,5x – 3
|
2) у = –4x + 6
|
2) у = –х
|
||||||||||||||||||
|
|
||||||||||||||||||||
Завдання 966
При якому значенні b графіки функцій у = 1,5x – 3, у = 2,5x + 1 і у = 5x + b перетинаються в одній точці?
1,5х – 3 = 2,5х + 1; 2,5х – 1,5х = –3 – 1; х = –4; у = 1,5 • (–4) – 3 = –9.
Підставимо координати (–4;–9) у рівняння третьої прямої: –9 = 5 • (–4) + b; b = 11
Отже, при b = 11 дані три графіки функцій перетинаються в одній точці.
Завдання 997
Точка C належить відрізку AB завдовжки 8. Довжина відрізка AC дорівнює x, довжина відрізка BC — у. Побудуйте графік залежності у від x, якщо 0 < x < 8. Позначте на цьому графіку точку, яка відповідає випадку, коли точка C — середина відрізка AB.
у + х = 8; Звідси у = –х + 8
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
у |
8 |
7 |
6 | 5 | 4 | 3 | 2 | 1 | 0 |
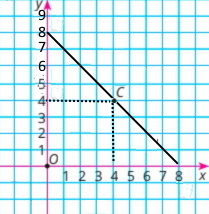
Середина відрізка, тому у = х., отже, х = –х + 8; 2х = 8; х = 4
Якщо х = 4, тоді у = –х + 8 = –4 + 8 = 4
Точка С(4;4) – середина відрізка АВ.
Завдання 998
Периметр прямокутника ABCD дорівнює 12, AB = x, AD = у, 0 < x < 6. Побудуйте графік залежності у від x. Позначте на цьому графіку точку, яка відповідає випадку, коли прямокутник ABCD є квадратом.
Периметр дорівнює 12, тобто 2(х + у) = 12; х + у = 6, у = 6 – х
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
у |
6 |
5 |
4 | 3 | 2 | 1 | 0 |
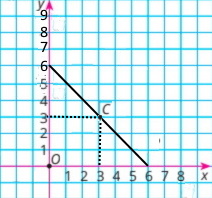
Прямокутник квадрат, коли у = х, тому х = 6 – х; 2х = 6; х = 3
Якщо х = 3, тоді у = 6 – х = 6 – 3 = 3
Точка С(3;3) відповідає випадку, коли прямокутник ABCD – квадрат.
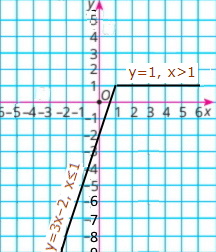
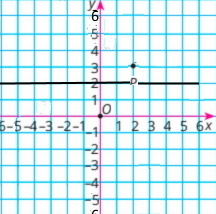
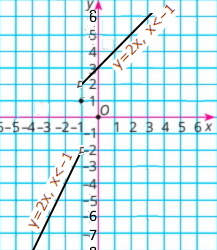
Завдання 999 Побудуйте графік функції:
|
1) у = {х – 4, якщо х ≥ 0 –2х – 4, якщо х < 0 |
3) у = {2, якщо х ≠ 2 3, якщо х = 2 |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
 |
|||||||||||||||||||||
|
2) у = {3х – 2, якщо х ≤ 1 1, якщо х > 1
|
4) у = {2х, якщо х < –1 1, якщо х = –1 х + 3, якщо х > –1 |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
 |
|||||||||||||||||||||
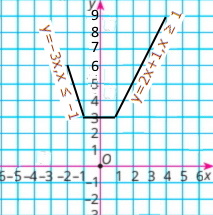
Завдання 1000 Побудуйте графік функції
|
1) у = {–3х, якщо х ≤ –1, 3, якщо –1 < х < 1 2х+1, якщо х ≥ 1 |
2) y = {5 – х, якщо х ≤ 3 x + 1, якщо х > 3 |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
Завдання 1001
|
1) у = |x| |
2) у = |x| + x |
3) у = 4x – |x| + 2 |
|
|
|
|
Завдання 1002
|
1) у = –|x| |
2) у = x – |x| |
3) у = 3x + 2|x| |
|
|
|
|
Завдання 1003
Формули лінійних функцій, графіки яких:
|
на рисунку 47 |
на рисунку 48 |
|
1) пряма a; у = х + 3 2) пряма b. y = –0,5x – 1 |
1) пряма m; y = –2/3x 2) пряма n. у = 2х – 4 |
Завдання 1005
Функцію задано описом: значення функції дорівнює різниці між значенням аргументу й цілою частиною аргументу: у = х – [x]
Побудуйте графік цієї функції.
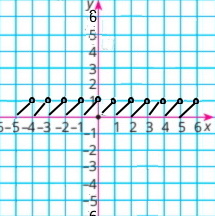
Примітка: за допомогою запису [х] позначають найбільше ціле число, яке не більше за х
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 1006
Троє друзів вирішили створити фірму з виробництва меблів і домовилися ділити прибуток пропорційно своїм внескам до статутного капіталу фірми. Один із них уніс 75 000 грн, другий — 125 000 грн, а третій — 175 000 грн. За підсумками першого року роботи прибуток склав 1 800 000 грн. Скільки грошей має отримати кожен із друзів?
Розв'язання
175 000 : 125 000 : 75 000 = 7 : 5 : 3
1) 7 + 5 + 3 = 15 (ч.) – всього частин;
2) 3/15 • 1 800 000 = 1/5 • 1 800 000 = 360 000 – отримає перший друг;
3) 5/15 • 1 800 000 = 1/3 • 1 800 000 = 600 000 – отримає другий друг;
4) 7/15 • 1 800 000 = 840 000 – отримає третій друг.
Відповідь: 360 000 грн; 600 000 грн; 840 000 грн.
Завдання 1007 Вирази
1) (2 + 3a)(5 – a) – (2 – 3a)(5 + a) = 10 + 15a – 2a – 3a² – 10 – 2a + 15a + 3a² = 26a
Якщо a = –1,5, тоді 26a = 26 • (–1,5) –39
2) (3a + b)² –(3a –b)² = 9a² + 6ab + b² – 9a² + 6ab – b² = 12ab
при a = –3 1/3, b = 0,3: 12ab = 12 • (–3 1/3) • 0,3 = –12
Завдання 1008 Рівняння
|
1) (5x + 1)(2х – 3) = (10x – 9)(x + 2) 10x² – 15х + 2х – 3=10x² + 20х – 9х – 18 |
2) (7x – 1)(х + 5) = (3 + 7x)(x + 3) |
Завдання 1009
Доведіть, що сума кубів трьох послідовних натуральних чисел ділиться націло на 3.
Нехай n – 1, n, n + 1 – три послідовні натуральні числа.
(n – 1)3 + n3 + (n + 1)3 = n3 – 3n2 + 3n – 1 + n3 + n3 + 3n2 + 3n + 1 =
= 3n3 + 6n – 3(n3 + 2n) Отриманий вираз ділиться без остачі на 3, отже, твердження задачі доведено.
Завдання 1010
У двох діжках було порівну води. Об’єм води в першій діжці спочатку збільшили на 10 %, а потім зменшили на 10 %. Об’єм води в другій діжці, навпаки, спочатку зменшили на 10 %, а потім збільшили на 10 %. У якій діжці води стало більше?
Розв'язання
Нехай воли в обох діжках було по х л.
У першій діжці після збільшення на 10% води стало (х + 0,1х) = (1 + 0,1)х = 1,1х л,
а після зменшення на 10% води стало 0,9 • 1,1х = 0,99х л.
У другій діжці після зменшення на 10% води стало (х – 0,1х) = (1 – 0,1)х = 0,9х л,
а після збільшення на 10% води стало 0,9х • 1,1х = 0,99х л.
Отже, у двох діжках залишилося порівну води.
Відповідь: порівно.
Завдання 1011
Відомо, що x² + у² = a, xy = b. Чому дорівнює значення виразу x4 + x²у² + у4?
x4 + x²y² + y4 = x4 + 2x²y² + y4 – x²y² = (x² + y²)² – x²y² = a² – b²
Завдання 1012
Доведіть, що при будь–якому значенні x значення виразу |x| – x більше за відповідне значення виразу 2x – x² – 2.
Значення виразу |х| – х завжди невід'ємне.
Перетворимо другий вираз: 2х – х² – 2 = –1 – (х² – 2х + 1) = –1 – (х – 1)².
Значення цього виразу завжди від'ємне. Тому твердження задачі доведено.
Завдання 1013
1) Якщо х = –4, у = 0,6, то 0,1х + 5у = 0,1 • 4 + 5 • 0 6 = –0,4 + 3 = 2,6
якщо х = 6, у = –2, то х² – 3у + 7 = 6² – 3 • 2 + 7 = 36 + 6 + 7 = 49
3) якщо х = –10, у = 2, то |х| + |у + 6| = |–10| + |2 + 6| = 10 + 8 = 18
4) якщо х = –4, у = 1,5, то (2у – 3)² – (х + 4)² = (2 • 1,5 – 3)² – (–4 + 4)² = 0² – 0² = 0
Завдання 1014
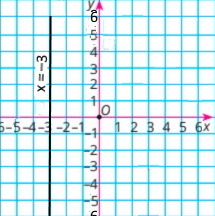
Зобразіть на координатній площині всі точки (x;у) такі, що:
|
1) x = –3 |
2) у = 2 |
3) x = 0 |
|
|
|
|
Завдання 1015
Є два друкарських автомати. Перший, отримавши на вході картку із числами (a; b; c), видає на виході картку із числами ((a + b)/2 ; (b + c)/2 ; (a + c)/2), а другий за карткою із числами (a; b; c) — картку із числами (2a – b; 2b – c; 2c – a). Чи можна за допомогою цих автоматів з картки із числами (2,8; –1,7; 16) отримати картку із числами (1,73; 2; 0,4)?
Обидва автомати замінюють трійку чисел а, b, с картки новою трійкою, але з тією самою сумою чисел (а + b + с). Указані картки, які потрібно отримати, мають різні суми чисел. Тому, за такою процедурою, необхідну картку отримати неможливо.