Завдання 353
Олена та Ігор планують подорож із Кракова до Риму. На сайті різних перевізників для цієї подорожі вони знайшли 2 авіарейси, 3 залізничних маршрути та 4 автобусних маршрути. Скількома способами Олена та Ігор зможуть здійснити цю подорож?
Розв'язання
За правилом додавання маємо:
2 + 3 + 4 = 9 (сп.)
Відповідь: Олена та Ігор зможуть здійснити цю подорож 9 способами.
Завдання 354
Катерина зайшла в кафе і побачила у меню 5 видів кави, 4 види чаю та 10 різновидів тортів і тістечок. Скількома способами дівчина може сформувати замовлення, якщо обере з меню один гарячий напій та один десерт?
Розв'язання
За правилом додавання маємо:
1) 5 + 4 = 9 (сп.) – обере напій;
За правилом добутку маємо:
2) 9 • 10 = 90 (сп.) – обере замовлення;
Відповідь: дівчина може сформувати замовлення 90 способами.
Завдання 355
Скільки можна утворити чотирицифрових чисел із цифр 2, 4, 6, 8, якщо ці цифри можуть повторюватися?
Розв'язання
Кожну з цифр чотирицифрового числа можна обрати 4 способами, тому за правилом добутку маємо:
4 • 4 • 4 • 4 = 256 (сп.)
Відповідь: можна утворити 256 способами.
Завдання 356
У репертуарі оперного театру протягом місяця є 6 балетних вистав, 8 опер, 2 оперети та одна музична казка. Скількома способами відвідувачі та відвідувачки можуть обрати один із цих заходів? Скільки існує способів переглянути покази по одному кожного виду?
Розв'язання
За правилом додавання маємо:
1) 6 + 8 + 2 + 1 = 17 (сп.) – обрати один із цих заходів;
За правилом добутку маємо:
2) 6 • 8 • 2 = 96 (сп.) – переглянути покази по одному кожного виду.
Відповідь: 17 способів; 96 способів.
Завдання 357
Учні та учениці 6 класів організували благодійний ярмарок, на якому продавали 15 видів випічки, 8 видів фруктів та 5 видів напоїв. Скількома способами можна здійснити покупку одного товару? Скільки існує способів обрати покупку по одному з трьох товарів?
Розв'язання
За правилом додавання маємо:
1) 15 + 8 + 5 = 28 (сп.) – здійснити покупку одного товару;
За правилом добутку маємо:
2) 15 • 8 • 5 = 600 (сп.) – обрати покупку по одному з трьох товарів.
Відповідь: 17 способів; 96 способів.
Завдання 358
Скільки можна утворити різних п’ятицифрових чисел із цифр 1, 3, 5, 7, 9, якщо ці цифри не можуть повторюватися?
Розв'язання
Для вибору першої цифри п'ятицифрового числа існує 5 способів, для другої – 4 способи, для третьої – 3 способи, для другої – 2 способи, для третьої – 1 спосіб, тому за правилом добутку маємо:
5 • 4 • 3 • 2 • 1 = 120 (ч.) – п'ятицифрових чисел можна утворити.
Відповідь: 120 чисел.
Завдання 359
Пані Вікторія забула семизначний код, що було встановлено на замок її валізи. Скільки існує можливих кодів, якщо використовуються цифри від 1 до 7 і в установленому коді жодна цифра не повторюється?
Розв'язання
За правилом добутку маємо:
7 • 6 • 5 • 4 • 3 • 2 • 1 = 5040 (к.) – можливих кодів.
Відповідь: 5040 кодів.
Завдання 360
Олег вирішив зіграти в лотерею та мав обрати 10 чисел у діапазоні від 1 до 80. Визначте, скільки є способів заповнення лотерейного квитка, якщо числа не можуть повторюватися.
Завдання 361
Діти мають вгадати трицифрове число, яке складається із цифр: 1, 3, 5, 7, 9. Відомо, що цифри в числі не повторюються. Спочатку діти назвали число 375 і виявилося, що вони вгадали дві цифри, і тільки одна з них стоїть на своєму місці. Потім діти назвали 571 і виявилося, що вгадано дві цифри, і дві з них стоять на своїх місцях. Допоможіть дітям знайти число, яке загадала вчителька. 579
Завдання 362 Середнє арифметичне
Знайдіть середнє арифметичне поданих чисел.
Розв'язання
а) (124 + 323 + 152 + 247 + 388 + 244 + 97) : 7 = 1575 : 7 = 225
б) (2 1/5 + 4,1 + 6 1/2 + 9 7/10 + 7 2/5 + 6,7) : 6 =
= (2,2 + 4,1 + 6,5 + 9,7 + 7,4 + 6,7) : 6 = 36,6 : 6 = 6,1
Відповідь: а) 225; б) 6,1.
Завдання 363
Середнє арифметичне трьох чисел становить 135. Знайдіть третє число, як що відомо два інших – 120 і 145.
Розв'язання
(120 + 145 + х) : 3 = 135
120 + 145 + х = 405
х = 405 – 120 – 145
х = 140
Відповідь: третє число 140.
Завдання 364
Знайдіть середню температуру повітря протягом тижня за даними в таблиці.
Розв'язання
(20 + 17 + 19 + 22 + 21 + 20 + 21) : 7 = 140 : 7 = 20 (°С)
Відповідь: середня температура повітря 20°С.
Завдання 365
Турист рухався по дорозі протягом двох годин зі швидкістю 8 км/год. Одну годину йшов під гору зі швидкістю 4,6 км/год та ще годину йшов із гори зі швидкістю 6,8 км/год. Визначте, з якою середньою швидкістю рухався турист
Розв'язання
1) 8 • 2 = 16 (км) – пройшов за перші дві години;
2) 4,6 • 1 = 4,6 (км) – пройшов за третю годину;
3) 6,8 • 1 = 6,8 (км) – пройшов за четверту годину.
4) (16 + 4,6 + 6,8) : 4 = 27,4 : 4 = 6,85 (км/год)
Відповідь: турист рухався з середньою швидкістю 6,85 км/год.
Завдання 366
Знайдіть середнє арифметичне шести чисел, якщо відомо, що середнє арифметичне чотирьох із них дорівнює 7,7, а середнє арифметичне двох інших чисел дорівнює 6,5.
Розвязання
1) 6,5 • 2 = 13 – сума двох чисел;
2) 7,7 • 4 = 30,8 – сума чотирьох чисел.
3) (13 + 30,8) : 6 = 43,8 : 6 = 7,3
Відповідь: середнє арифметичне шести чисел 7,3.
Завдання 367
На фермі народилося 6 поросят: два з них вагою по 1,2 кг, решта – 1,4 кг, 1,3 кг, 1,1 кг, 1,0 кг. Знайдіть середню вагу одного поросяти.
Розвязання
1) 1,2 • 2 = 2,4 (кг) – маса двох поросят.
2) (2,4 + 1,4 + 1,3 + 1,1 + 1,0) : 6 = 7,2 : 6 = 1,2 (кг)
Відповідь: середня вага поросяти 1,2 кг.
Завдання 368
Середній вік дванадцяти гравчинь збірної команди з волейболу становить 26,5 років. Коли до складу збірної взяли ще одну гравчиню, то середній вік став 27 років. Визначте, скільки років гравчині, яку взяли до команди останньою.
Розвязання
1) 26,5 • 12 = 318 (р.) – сума років 12-ти гравчинь;
2) 27 • 13 = 351 (р.) – сума років 13-ти гравчинь.
3) 351 – 318 = 33 (р.)
Відповідь: гравчині, яку взяли в команду останньою, 33 роки.
Завдання 369
Найменшими були витрати у вівторок, а найбільшими - у п'ятницю.
1) 25,5 + 22,4 + 24,6 + 27,5 + 30 = 130 (грн) – загальна сума витрачених грошей.
2) 130 : 5 = 26 (грн) – середня вартість обіду.
Відповідь: 130 грн; 26 грн.
Завдання 370
Побудуйте лінійну діаграму за цими даними та визначте день найменшої активності. Якою є щоденна середня кількість кроків?
Розвязання
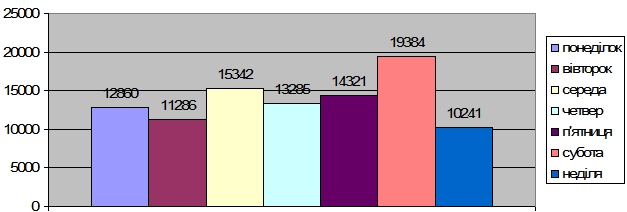
День найменшої активності: неділя.
(12860 + 11286 + 15342 + 13285 + 14321 + 19384 + 10241) : 7 = 96719 : 7 =
= 13817 (кр.) – щоденна середня кількість кроків.
Відповідь: 12817 кроків.
Завдання 371
За результатами контрольної роботи з математики вчителька створила кругову діаграму успішності тридцяти учнів та учениць шостого класу.
Розвязання
1) 30 • 0,1 = 3 (уч.) – початковий рівень або не писали;
2) 30 • 0,3 = 9 (уч.) – середній рівень або достатній рівень;
3) 30 • 0,2 = 280 (уч.) – високий рівень.
Завдання 372
Проаналізуйте дані про те, скільки учнів та учениць класу відвідує одну або більше спортивних секцій. Побудуйте діаграму довільного виду, яка ілюструватиме дані, що наведено у таблиці.
Розвязання
1) 24 + 9 + 3 = 36 (д.) – всього дітей;
2) 24/36 • 360° = 240° – жодна секція;
3) 9/36 • 360° = 90° – одна секція;
4) 3/36 • 360° = 30° – дві і більше.
Завдання 373
У шухляді лежать кубики синього і жовтого кольорів. Визначте, скільки у шухляді синіх кубиків, якщо жовтих у ній 9, а ймовірність того, що вибраний кубик жовтого кольору, дорівнює 3/5. Яка ймовірність того, що навмання витягнутий із шухляди кубик буде синього кольору? Яка із цих двох подій буде більш імовірною?
Розвязання
За умовою Р(А) = 3/5 = 9/15, тому загальна кількість кубиків 15.
15 – 9 = 6 (к.) – синіх кубиків, тому ймовірність того, що витягнутий кубик буде синього кольору 6/15.
Оскільки 9/15 > 6/15, тому більш ймовірно витягнути жовтий кубик, ніж синій.
Відповідь: 6 кубиків; більш ймовірно витягнути жовтий кубик.