Завдання 1935
120 : 2 = 60 — половина від 120
120 : 3 = 40 — третина від 120
120 : 10 = 12 — десята частина від 120
Завдання 1936
На скільки третина числа 108 більша за його четверту частину?
108 : 3 = 36 — це третина від 108
108 : 4 = 27 — це четверта частина від 108
108 : 3 > 108 : 4 на 9, бо 36 – 27 = 9
Відповідь: на 9.
Завдання 1937
На скільки 0,7 числа 126 більше від 0,3 цього числа?
126 • 0,7 = 88,2 — це 0,7 числа 126
126 • 0,3 = 37,8 — це 0,3 числа 126
126 • 0,7 > 126 • 0,3 на 50,4, бо 88,2 – 37,8 = 50,4
Відповідь: на 50,4.
Завдання 1938
а) 2,6 • 0,2 = 0,52 — це 0,2 числа 2,6
2,3 • 0,3 = 0,69 — це 0,3 числа 2,3
2,6 • 0,2 < 2,6 • 0,3
|
б) 0,8 • 0,6 = 0,48 — це 0,6 числа 0,8
0,6 • 0,8 = 0,48 — чи 0,8 числа 0,6
0,8 • 0,6 = 0,8 • 0,6
|
Завдання 1939
В одній крамниці тато витратив 0,3 грошей, що мав, а в другій — ще 470 грн. У нього залишилося 1000 грн. Скільки гривень він витратив в обох крамницях разом?
Розв'язання
Нехай тато мав х грн, тоді у першій крамниці він витратив 0,3х грн. Складаємо рівняння.
х – 0,3х – 470 = 1000
0,7х = 1470
х = 1470 : 0,7
х = 2100 (грн) – мав грошей;
0,3х = 0,3 • 2100 = 630 (грн) – витратив в першій крамниці;
630 + 470 = 1100 (грн) – витратив в обох крамницях.
Відповідь: 1100 грн.
Завдання 1940
З діжки відлили спочатку 0,5, а потім — 0,3 всієї олії, що була в ній, після чого в діжці залишилося 30 л олії. Скільки літрів олії було в діжці спочатку?
Розв'язання
Нехай було х л олії, тоді відлили спочатку 0,5х л, а потім 0,3х л. Складаємо рівняння.
х – 0,5х – 0,3х = 30
0,2х = 30
х = 30 : 0,2
х = 150
Відповідь: 150 л.
Завдання 1941
З каси видали 0,3 усіх наявних грошей, потім — половину остачі, після чого в ній залишилося 3500 грн. Скільки грошей було в касі спочатку?
Розв'язання
Нехай було в касі х грн, тоді видали 0,3х, а потім 0,7х : 2 = 0,35х грн. Складаємо рівняння.
х – (0,3х + 0,35х) = 3500
0,35х = 3500
х = 3500 : 0,35
х = 10 000
Відповідь: 10 000 грн.
Завдання 1942
Три десятих відстані між містами на 26 км менші за решту відстані. Знайди відстань між цими містами.
Розв'язання
Нехай відстань становитьі х км, тоді 0,3х менша за решту 0,7х відстані на 26 км. Складаємо рівняння.
0,7х – 0,3х = 26
0,4х = 26
х = 26 : 0,4
х = 65
Відповідь: 65 км.
Завдання 1943
Скільки дощок піде на настилання підлоги в кімнаті, довжина якої 3,5 м, а ширина — 3,2 м, якщо довжина кожної дошки дорівнює 4,5 м, а ширина становить 0,04 довжини?
Розв'язання
1) 3,5 • 3,2 = 11,2 (м2) – площа підлоги;
2) 4,5 • 0,04 = 0,18 (м) – ширина дошки;
3) 4,5 • 0,18 = 0,81 (м) – площа дошки;
4) 11,2 : 0,81 = 13,8 ≈ 14 (д.) – дощок піде на настилання підлоги.
Відповідь: 14 дощок.
Завдання 1944
Присадибна ділянка має форму прямокутника, довжина якого 120 м, а ширина — 90 м. Під картоплю відведено 0,75 усієї площі, решту — під інші овочі. Яку площу відведено під картоплю?
Розв'язання
1) 120 • 90 = 10800 (м2) – площа ділянки;
2) 10800 • 0,75 = 8100 (м2) – площа під картоплею.
Відповідь: 8100 м2.
Завдання 1945
У господарстві виростили 2400 саджанців, з яких 0,3 становили липи, а 0,4 решти саджанців — клени. На скільки саджанців кленів виростили більше чи менше, ніж саджанців липи?
Розв'язання
1) 2400 • 0,3 = 720 (с.) – липи;
2) 2400 – 720 = 1680 (с.) – решта;
3) 1680 • 0,4 = 672 (с.) – клени;
4) 720 – 672 = 48 (с.) – на стільки більше саджанців липи.
Відповідь: на 48 саджанців.
Завдання 1946
На будівництво привезли 490 т будівельних матеріалів: 0,1 їх становить вапно, 0,2 — цемент, решта — цегла. Скільки тонн цегли привезли на будівництво?
Розв'язання
1) 490 • 0,1 = 49 (т) – вапно;
2) 490 • 0,2 = 98 (т) – цемент;
3) 490 – (49 + 98) = 343 (т) – решта.
Відповідь: 343 т.
Завдання 1947
Накресли відрізок AB завдовжки 38 мм.
Завдання 1948
Накресли відрізок KP і познач на ньому точку T. Виміряй довжини всіх відрізків, які утворилися.
Завдання 1949
Накресли прямокутник зі сторонами 46 і 33 мм. Обчисли його площу і периметр.
Розв'язання
1) 46 • 33 = 1518 (мм2) – площа прямокутника;
2) (46 + 33) • 2 = 79 • 2 = 158 (мм) – периметр прямокутника.
Відповідь: 1518 мм2 і 158 мм.
Завдання 1950
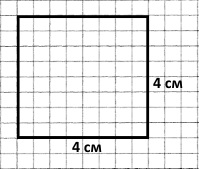
Накресли квадрат зі стороною 4 см. Обчисли його периметр і площу.
Розв'язання
1) 4 • 4 = 16 (см2) – площа квадрата;
2) 4 • 4 = 16 (см) – периметр квадрата.
Відповідь: 16 см2 і 16 см.
Завдання 1951
Накресли: а) гострий кут KOM; б) тупий кут P. Виміряй за допомогою транспортира їх міри.
Завдання 1952
Накресли за допомогою транспортира кути, які дорівнюють: 30°; 64°; 120°; 145°.
Завдання 1953
Накресли довільний трикутник. Виміряй за допомогою транспортира його кути і знайди їх суму.
∠А + ∠В + ∠С = 180°.
Завдання 1954
Накресли довільний чотирикутник. Виміряй за допомогою транспортира його кути і знайди їх суму.
∠А + ∠В + ∠С + ∠D= 320°.
Завдання 1955
Прямі AB і KP перетинаються в точці O так, що ∠AOK = 40°. Знайди міри кутів BOP, AOP і BOK.
∠BOP = ∠AOK = 40°; ∠AOP = 180° – ∠POB = 180° – 40° = 140°; ∠BOK = ∠AOP = 140°
Завдання 1956
Скільки вершин, ребер і граней має:
а) Куб має: вершин 8; ребер 12; граней 6.
б) Прямокутний паралелепіпед має: вершин 8; ребер 12; граней 6.
Завдання 1957
Кімната має виміри 4 м, 5 м і 4 м. Обчисли її об’єм.
Розв'язання
V = 4 • 5 • 4 = 80 (м3) – об'єм кімнати.
Відповідь: 80 см3.
Завдання 1958
Обчисли об’єм і площу поверхні куба, якщо його ребро завдовжки:
а) а = 4 см;
1) 4 • 4 • 4 = 64 (см3) – об'єм куба;
2) 4 • 4 • 6 = 96 (см2) – площа поверхні куба.
а) а = 5 дм;
1) 5 • 5 • 5 = 125 (см3) – об'єм куба;
2) 5 • 5 • 6 = 150 (см2) – площа поверхні куба.
в) x м.
1) х • х • х = х3 (м3) – об'єм куба;
2) х • х • 6 = 6х2 (м2) – площа поверхні куба.
Завдання 1959
Обчисли площу поверхні та об’єм куба, якщо площа однієї його грані дорівнює 36 см2.
Розв'язання
1) 36 • 6 = 216 (см2) – площа поверхні куба;
2) 36 = 6 • 6, тому 6 (см) – довжина ребра куба;
3) 36 • 6 = 216 (см3) – об'єм куба.
Відповідь: 216 см2; 216 см3.
Завдання 1960
Знайди суму довжин усіх ребер та об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 3 см, 4 см і 5 см.
Розв'язання
1) (3 + 4 + 5) • 4 = 12 • 4 = 48 (см) – сума довжин усіх ребер;
2) 3 • 4 • 5 = 60 (см2) – об'єм прямокутного паралелепіпеда.
Відповідь: 48 см; 60 см2.
Завдання 1961
Сторона квадрата на 2,5 см більша від сторони рівностороннього трикутника з периметром 21 см. Знайди периметр і площу квадрата.
Розв'язання
1) 21 : 3 = 7 (см) – сторона трикутника;
2) 7 + 2,5 = 9,5 (см) – сторона квадрата;
3) 9,5 • 4 = 38 (см) – периметр квадрата;
4) 9,5 • 9,5 = 90,25 (см2) – площа квадрата.
Відповідь: 38 см; 90,25 см2.
Завдання 1962
Скільки тонн пшениці можна насипати в кузов автомобіля завдовжки 4 м, завширшки 2 м 50 см і глибиною 80 см, якщо маса 1 м3 зерна становить 0,7 т?
Розв'язання
1) 4 • 2,5 • 0,8 = 8 (м3) – об'єм кузова;
2) 0,7 • 8 = 5,6 (т) – пшениці можна еасипати в кузов.
Завдання 1963
В акваріум, довжина якого 6 дм, ширина — 4 дм, висота — 4 дм, налили воду до висоти 30 см. Скільки літрів води налили в акваріум? А скільки можна ще налити?
Розв'язання
1) 6 • 4 • 4= 96 (дм3) – об'єм акваріума;
2) 6 • 4 • 3= 72 (дм3) – об'єм води;
3) 96 – 72 = 24 (дм3) – можна налити води.
Відповідь: 24 дм3.
Завдання 1964
Читальний зал має розмір 9,4 × 6 × 4,5 м. На скільки місць розрахований читальний зал, якщо одній людині потрібно 3 м3 повітря?
Розв'язання
1) 9,4 • 6 • 4,5 = 253,8 (м3) – об'єм повітря;
2) 253,8 : 3 = 84,6 (м.) – місць в читальному залі.
Завдання 196 5
Прямокутний паралелепіпед, який має довжину 12 см, ширину 8 см і висоту 4 см, розрізали на кубики з ребром 1 см. Скільки таких кубиків одержали?
Розв'язання
1) 12 • 8 • 4 = 384 (см3) – об'єм пралелепіпеда;
2) 384 : 1 = 384 (к.) – одержали кубиків.
Завдання 1966 Чи може трикутник мати сторони:
а) 3; 6 і 9 см; Не може.
б) 5,3; 3,5 і 8 дм; Може бути.
в) 6; 2,4 і 6,5 м? Може бути.
Завдання 1967 Яка з трьох точок A, B, C лежить між двома іншими, якщо:
а) AB = 15 см, AC = 19 см і CB = 4 см; Точка В.
б) AB = 18 см, AC = 12 см і BC = 6 см; Точка С.
в) AB = 3 см, BC = 4 см і AC = 7 см? Точка В.
Завдання 1968
У прямокутному трикутнику дві сторони, що утворюють прямий кут, мають довжини 10 і 15 см. Знайди площу трикутника.
Розв'язання
(10 • 15) : 2 = 150 : 2 = 75 (см2) – площа трикутника.