Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§6 Вертикальні кути, кут між двома прямими, що перетинаються
Завдання 113
Пари вертикальних кутів: ∠PMA і ∠FMT, ∠AMF і ∠PMT.
Завдання 114
Вертикальних кутів нема.
Завдання 115
1) Один з вертикальних кутів дорівнює 15°. Знайдіть другий кут.
Два вертикальні кути різної пари є суміжними, тобто утворюють розгорнутий кут, тому
180° – 15° = 165° – другий кут.
Відповідь: кут 165°.
2) Один з вертикальних кутів дорівнює 129°. Знайдіть другий кут.
Два вертикальні кути різної пари є суміжними, тобто утворюють розгорнутий кут, тому
180° – 129° = 51° – другий кут.
Відповідь: кут 51°.
Завдання 116
1) Один з вертикальних кутів дорівнює 42°. Знайдіть другий кут.
Два вертикальні кути різної пари є суміжними, тобто утворюють розгорнутий кут, тому
180° – 42° = 138° – другий кут.
Відповідь: кут 138°.
2) Один з вертикальних кутів дорівнює 139°. Знайдіть другий кут.
Два вертикальні кути різної пари є суміжними, тобто утворюють розгорнутий кут, тому
180° – 139° = 41° – другий кут.
Відповідь: кут 41°.
Завдання 117
Усі пари вертикальних кутів:
∠APB і ∠LPM (або ∠BPA і ∠MPL);
∠BPC і ∠KPL (або ∠CPB і ∠LPK);
∠APC і ∠KPM (або ∠CPA і ∠MPK);
∠APK і ∠CPM (або ∠KPA і ∠MPC)
Завдання 118
Один з кутів, що утворилися при перетині двох прямих, дорівнює 40°. Знайдіть інші кути.
При перетині двох прямих утворюється дві пари вертикальних кутів, які є рівними.
Одна пара вертикальних кутів по 40°.
Різної пари вертикальні кути утворюють суміжний кут, тому 180° – 40° = 140° – інший вертикальний кут.
Друга пара вертикальних кутів по 140°.
Відповідь: 40° і 40°, 140° і 140°.
Завдання 119
∠AML = 120°. Знайдіть ∠AMP, ∠PMB і ∠BML.
Кути AML і PMB – вертикальні, тому вони рівні ∠AML = ∠PMB = 120°.
Вертикальні кути різних пар утворюють суміжний кут.
∠AMB = ∠AML + ∠LMB = ∠AML + ∠BML = 180°
∠BML = 180° – ∠AML = 180° – 120° = 60°.
Кути BML і AMP – вертикальні, тому вони рівні. ∠BML = ∠AMP = 60°.
Відповідь: ∠AMP = 60°, ∠PMB = 120° і ∠BML = 60°.
Завдання 120
Учениця накреслила дві прямі, що перетинаються, та, вимірявши транспортиром один з кутів, які при цьому утворилися, отримала 130°. Чи може вона стверджувати, що кут між прямими дорівнює 130°?
Ні. Кут між прямими не перевищує 90°.
Оскільки вертикальні кути різних пар є суміжними, то в даному випадку кут між прямим дорівнює 180° – 130° = 50°.
Завдання 121
Прямі AB і PL перетинаються в точці O. ∠POB = 118°. Знайдіть кут між прямими AB і PL.
Вертикальні кути різних пар є суміжними, утворюють розгорнутий кут.
∠POL = ∠POB + ∠BOL = 180°
Кутом між прямими буде менший вертикальний кут.
∠BOL = 180° – ∠POB = 180° – 118° = 62°
Відповідь: кут між прямими 62°.
Завдання 122
Накресліть дві прямі, що перетинаються, та знайдіть за допомогою транспортира кут між ними.
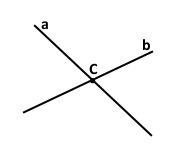
Кут між прямим не може перевищувати 90° (менший у парах вертикальних кутів).
У нашому випадку кут між прямими дорівнює 70°.
Завдання 123
Накресліть MON, що дорівнює 110°. Побудуйте доповняльні промені OL і OK до його сторін OM і ON відповідно. Обчисліть градусні міри трьох нерозгорнутих кутів, що утворилися, і порівняйте з результатами вимірювання.
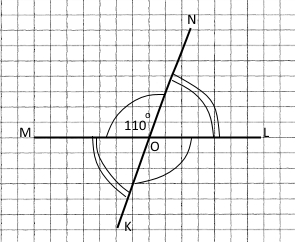
Кути MON і LOK вертикальні, тому ∠MON = ∠LOK = 110°
Вертикальні кути різної пари є суміжними, утворюють розгорнутий кут:
∠MOL = ∠MON + ∠NOL = 180°
∠NOL = 180° – ∠MON
∠NOL = 180° – 110° = 70°.
Вертикальні кути рівні, утворюють пару, ∠NOL = ∠MOK = 70°.
Відповідь: ∠LOK = 110°, ∠NOL = 70°, ∠MOK = 70°.
Завдання 124
Накресліть ∠AOB, що дорівнює 30°. Побудуйте доповняльні промені OP і OD до його сторін OA і OB відповідно. Обчисліть градусні міри трьох нерозгорнутих кутів, що утворилися, і порівняйте з результатами вимірювання.
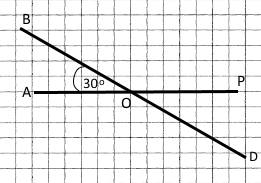
Кути AOB і POD вертикальні, тому ∠AOB = ∠POD = 30°
Вертикальні кути різної пари є суміжними, утворюють розгорнутий кут:
∠AOP = ∠AOB + ∠BOP = 180°
∠BOP = 180° – ∠AOB
∠BOP = 180° – 30° = 150°.
Вертикальні кути рівні, утворюють пару, ∠BOP = ∠AOD = 150°.
Відповідь: ∠POD = 30°, ∠BOP = 150°, ∠AOD = 150°.
Завдання 125
1) Знайти градусну міра кожного з кутів, які утворилися при перетині двох прямих, якщо усі кути рівні між собою.
Вертикальні кути різної пари є суміжними, утворюють розгорнутий кут. Якщо усі кути рівні, тоді 180° : 2° = 90°
Відповідь: 90°, 90°, 90°, 90°.
2) Градусна міра кожного з кутів, які утворилися при перетині двох прямих, якщо сума двох з них дорівнює 178°.
Оскільки сума величин двох кутів не дорівнює величині розгорнутого кута, то відома сума вертикальних кутів, а не суміжні. Вертикальні кути рівні.
178° : 2 = 89° – один вертикальний кут.
Вертикальні кути різних пар є суміжними, тобто утворюють розгорнутий кут, тому
180° – 89° = 91° – інший вертикальний кут.
Відповідь: 89°, 89°, 91°, 91°.
Завдання 126
1) Знайдіть градусну міру кожного з кутів, які утворилися при перетині двох прямих, якщо сума двох з них дорівнює 16°;
Оскільки сума величин двох кутів не дорівнює величині розгорнутого кута, то відома сума вертикальних кутів, а не суміжні.
Вертикальні кути рівні. 16° : 2 = 8° – один вертикальний кут.
Вертикальні кути різних пар утворюють суміжний кут, тому
180° – 8° = 172° – інший вертикальний кут.
Відповідь: 8°, 8°, 172°, 172°.
2) Знайдіть градусну міру кожного з кутів, які утворилися при перетині двох прямих, якщо три із чотирьох кутів рівні між собою.
При перетині двох прямих утворюються попарно рівні вертикальні кути. Якщо три із чотирьох кутів рівні, тоді їм дорівнює четвертий кут.
Вертикальні кути різних пар є суміжними, тобто утворюють розгорнутий кут, тому
180° : 2 = 90° – вертикальні кути усіх пар.
Відповідь: 90°, 90°, 90°, 90°.
Завдання 127
1) Знайдіть кут між прямими, що перетинаються, якщо різниця двох з утворених кутів дорівнює 18°.
Якщо різниця двох з утворених кутів дорівнює 18°, це означає, що один із кутів на 18° більший від другого. Вертикальні кути різних пар є суміжними, тобто сума таких вертикальних кутів утворює розгорнутий кут (дорівнює 180°).
Нехай х (°) – один вертикальний кут, тоді х + 18 (°) – інший вертикальний кут. Складемо рівняння.
х + х + 18 = 180
2х = 180 – 18
2х = 162
х = 162 : 2
х = 81 (°) – шуканий кут, оскільки він менший за 90°.
Відповідь: кут 81°.
2) Знайдіть кут між прямими, що перетинаються, якщо сума трьох з утворених кутів дорівнює 293°.
Вертикальні кути різних пар є суміжними, утворюють розгорнутий кут, тому
293° – 180° = 113° – один вертикальний кут.
180° – 113° = 67° – шуканий кут між прямими (інший вертикальний кут, який є меншим серед вертикальних кутів).
Відповідь: 67°.
3) Знайдіть кут між прямими, що перетинаються, якщо один із кутів становить 4/5 від іншого.
Вертикальні кути різних пар суміжні, тобто вони утворюють розгорнутий кут і їхня сума дорівнює 180°.
Нехай х (°) – один кут, тоді х • 4/5 (°) – інший кут. Складемо рівняння.
х + х • 4/5 = 180
9/5 х = 180
х = 180 : 9/5
х = 180 • 5/9
х = 100 (°) – один кут.
4/5 х = 100 • 4/5 = 80 (°) – інший кут.
Оскільки кутом між прямими є менший із вертикальних кутів, шуканий кут між прямими дорівнює 80°.
Відповідь: кут 80°.
Завдання 128
1) Знайдіть кут між прямими, що перетинаються, якщо один з кутів, що утворилися, удвічі менший від іншого.
Вертикальні кути різних пар є суміжними, тому такі вертикальні кути утворюють розгорнутий кут, їхня сума дорівнює 180°.
Нехай х (°) – один вертикальний кут, тоді 2х (°) – інший вертикальний кут. Складемо рівняння.
х + 2х = 180
3х = 180
х = 180 : 3
х = 60 (°) – шуканий кут між прямими, оскільки він менший за 90°.
Відповідь: кут 60°.
2) Знайдіть кут між прямими, що перетинаються, якщо один з кутів становить 20% від іншого.
Вертикальні кути різних пар є суміжними, тому такі вертикальні кути утворюють розгорнутий кут, їхня сума дорівнює 180°.
Нехай х (°) – один вертикальний кут, тоді х : 100 • 20 = 0,2х (°) – інший вертикальний кут. Складемо рівняння.
х + 0,2х = 180
1,2х = 180
х = 180 : 1,2
х = 150 (°) – більший кут.
0,2х = 0,2 • 150 = 30 (°) – шуканий кут між прямими, оскільки він менший за 90°.
Відповідь: кут 30°.
Завдання 129
Прямі AP, BL і CK перетинаються в точці M, ∠BMC = 20°, ∠LMP = 60°. Знайдіть ∠AMK.
Між прямими, що перетинаються утворилися 3 пари вертикальних кути, які попарно рівні:
∠BMC = ∠KML, ∠CMP = ∠AMK, ∠PML = ∠AMB.
Вертикальні кути різних пар є суміжними, тобто утворюють розгорнутий кут.
∠BML = ∠BMC + ∠CMP + ∠PML = 180°
∠BMC + ∠CMP + ∠LMP = 180°
∠CMP = 180° – ∠BMC – ∠LMP = 180° – 20° – 60° = 100°.
Вертикальні кути рівні, тому ∠CMP = ∠AMK = 100°.
Відповідь: ∠AMK = 100°.
Завдання 130
Прямі AP, BL і CK перетинаються в точці M, ∠CMP = 105°, ∠KML = 25°. Знайдіть ∠AMB.
Між прямими, що перетинаються утворилися 3 пари вертикальних кутів:
∠BMC = ∠KML, ∠CMP = ∠AMK, ∠PML = ∠AMB.
Вертикальні кути різних пар є суміжними, тобто утворюють розгорнутий кут.
∠BML = ∠BMC + ∠CMP + ∠PML = 180°
∠KML + ∠CMP + ∠AMB = 180°
∠AMB = 180° – ∠KML – ∠CMP = 180° – 25° – 105° = 50°.
Відповідь: ∠AMB = 50°.
Завдання 131
На малюнку зображено три прямі, що перетинаються в одній точці. Знайдіть суму вертикальних кутів різних пар.
При перетині трьох прямих утвориться три пари вертикальних кутів.
Вертикальні кути різних пар є суміжними, тобто утворюють розгорнутий кут, тому сума таких кутів дорівнює 180°.
Відповідь: 180°.
Завдання 132
Доведіть, що бісектриси вертикальних кутів є доповняльними променями.
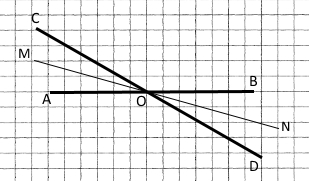
Пояснення.
Треба довести, що бісектриси вертикальних кутів є доповняльними променями, тобто мають спільний початок і лежать на одній прямій, тобто кут MON є розгорнутим (дорівнює 180°).
При перетині двох прямих утворилися суміжні кути СOВ і BOD, ∠СOА = ∠АBD, тобто вони утворюють розгорнуті кути ∠СOВ + ∠BOD = 180°, ∠СOА + ∠АOD = 180°.
За властивістю вимірювання кутів ∠MOD = ∠MOC + ∠COD, також ∠MOD = ∠MON + ∠NOD.
Якщо рівні ліві частини рівності, тоді також рівні праві частини, тому
∠MOC + ∠COD = ∠MON + ∠NOD, тоді ∠MON = ∠MOC + ∠COD – ∠NOD.
Нехай OM бісектриса вертикального кута АОС, тоді вона ділить його на два рівні кути ∠АОМ = ∠МОС, або ∠АОС = 2∠МОС.
Нехай ON бісектриса вертикального кута BОD, тоді вона ділить його на два рівні кути ∠BОN = ∠NOD, або ∠BOD = 2∠NOD.
При перетині двох прямих утворилися вертикальні кути ∠AOC = ∠BOD, ∠AOD = ∠BOC. Вони мають початком спільну точку О. Якщо рівні ліві частини рівності, тоді також рівні праві частини, тому ∠MOC = ∠NOD
∠MON = ∠MOC + ∠COD – ∠NOD = ∠MOC + ∠COD – ∠MOC = ∠COD = 180°
Отже, кут MON, утворений бісектрисами ОМ і ON, – розгорнутий, тобто бісектриси вертикальних кутів є доповняльними променями.
Дано ОМ і ОN бісектриси вертикальних кутів.
Доведення.
Нехай кути АОС і ВOD вертикальні. Оскільки кути СOВ і BOD суміжні, то ∠СOВ + ∠BOD = 180°. Оскільки кути СOА і AOD суміжні, то ∠СOА + ∠АOD = 180°.
Промінь OM – бісектриса кута АОС, тоді ∠АОС = 2∠МОС. Промінь ON – бісектриса кута BОD, тоді ∠BOD = 2∠NOD.
Вертикальні кути рівні ∠AOC = ∠BOD.
Якщо рівні ліві частини рівності, тоді також рівні праві частини, тому ∠MOC = ∠NOD
За властивістю вимірювання кутів ∠MOD = ∠MOC + ∠COD, також ∠MOD = ∠MON + ∠NOD.
Якщо рівні ліві частини рівності, тоді також рівні праві частини, тому
∠MOC + ∠COD = ∠MON + ∠NOD, тоді ∠MON = ∠MOC + ∠COD – ∠NOD.
∠MON = ∠MOC + ∠COD – ∠MOC = ∠COD = 180°
Отже, кут MON, утворений бісектрисами ОМ і ON, – розгорнутий.
Вправи для повторення
Завдання 133
На прямій послідовно позначено 10 точок так, що відстань між будь-якими двома сусідніми точками дорівнює 2 см. Знайдіть відстань між двома крайніми точками.
Між 10 точками на прямій є 9 відрізків, то 2 • 9 = 18 (см)
Відповідь: 18 см.
Завдання 134
Відомо, що ∠ABC = 70°, а ∠CBD = 20°. Знайти кут ABD.
І випадок
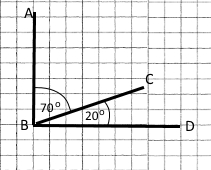
Спільний промінь ВС (кути знаходяться окремо).
∠ABD = ∠ABC + ∠CBD = 70° + 20° = 90°
ІІ випадок
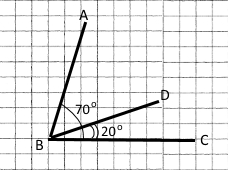
Спільний промінь BD (менший кут знаходиться у більшому).
∠ABC = ∠ABD + ∠DBC = ∠ABD + ∠CBD,
∠ABD = ∠ABC – ∠CBD = 70° – 20° = 50°
1) Чи може градусна міра кута ABD дорівнювати 40°? Ні.
2) Чи може градусна міра кута ABD дорівнювати 50°? Так.
3) Чи може градусна міра кута ABD дорівнювати 60°? Ні.
4) Чи може градусна міра кута ABD дорівнювати 80°? Ні.
5) Чи може градусна міра кута ABD дорівнювати 90°? Так.
6) Чи може градусна міра кута ABD дорівнювати 100°? Ні.
Життєва математика
Завдання 135 Згідно із санітарними нормами відношення площі вікон до площі підлоги у класній кімнаті має бути не менше ніж 0,2. Чи дотримано цих норм у класній кімнаті, довжина якої 14 м, а ширина становить 35 % від довжини, якщо в кімнаті три вікна розміром 2 х 1,8 м?
|
Для кімнати Довжина — 14 м Ширина — 35% довжини S — ? |
Для вікна Довжина — 2 м Ширина — 1,8 м S — ? |
Розв’язання
1) 14 : 100 • 35 = 4,9 (м) – ширина кімнати.
2) 14 • 4,9 = 68,6 (м2) – площа кімнати.
3) 2 • 1,8 = 3,6 (м2) – площа вікна.
4) 3,6 • 3 = 10,8 (м2) – площа трьох таких вікон.
5) 10,8 : 68,6 = 108 : 686 = 0,157 ≈ 0,16 (разів) – відношення площі вікон до площі підлоги у класній кімнаті.
0,16 < 0,20
Відповідь: не дотримано.
Завдання 136 Накресліть прямокутник ABCD та запишіть усі пари перпендикулярних прямих, які утворилися.
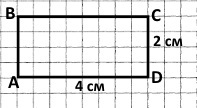
Чотири пари перпендикулярних прямих AB і АD; АВ і ВС; BC і СD; СD і АD.
Завдання 137 Фігуру на малюнку складено з восьми сірників.
1) Квадратів утворилося:
Короткий запис
З одної клітинки — 9 квадратів
З 4 клітинок — 4 квадрати
З 9 клітинок — 1 квадрат
Всього — ?
9 + 4 + 1 = 14 (кв.)
2) Як прибрати два сірники так, щоб залишилося лише три квадрати?
Перший зліва, перший знизу.
|_