
Завдання 1245
У легкоатлетичній секції тренуються 32 спортсмени, причому дівчат серед них на 4 більше, ніж хлопців. Скільки дівчат і скільки хлопців тренується в цій секції?
Розв'язання
Нехай у секції х дівчат і у хлопців, причому дівчат на 4 більше, тобто х – у = 4, а всіх дітей х + у = 32. Складаємо систему рівнянь:
{x + y = 32
x – y = 4
2x = 36
х = 36 : 2
х = 18
Підставимо знайдене значення х у рівняння х - 4 = 4:
18 – у = 4
у = 18 – 4
у = 14
Відповідь: у секції тренується 18 дівчат і 14 хлопців.
Завдання 1246
За дві години кухар наліпив 260 пельменів, причому за першу годину – на 20 пельменів менше, ніж за другу. Скільки пельменів наліпив кухар за першу годину і скільки – за другу?
Розв'язання
Нехай кухар за першу годину наліпив х пельменів, а за другу — y пельменів, причому за першу годину наліпив на 20 пельменів менше, тобто у – х = 20, а всього наліпив х + у = 260 пельменів. Складаємо систему рівнянь:
{у + х = 260
y – x = 20
2y = 280
у = 140
Підставимо знайдене значення у в рівняння у + х = 260:
140 + х = 260
х = 260 – 140
х = 120
Відповідь: кухар наліпив 120 пельменів за першу годину і 140 пельменів за другу годину.
Завдання 1247
За олівець і три зошити заплатили 32 грн, а за три олівці і зошит – 24 грн. Скільки коштує один олівець і скільки – один зошит?
Розв'язання
Нехай один олівець коштує x грн, а один зошит — y грн, тоді три олівці коштують 3х грн, а три зошити — 3у грн. Складаємо систему рівнянь:
{x + 3y = 32 |•(–3)
3x + y = 24
{–3x – 9y = –96
3x + y = 24
–8y = –72
у = (–72) : (–8)
y = 9
Підставимо знайдене значення у в рівняння х + 3у = 32:
x + 3 • 9 = 32
х + 27 = 32
х = 5
Відповідь: 5 грн коштує олівець і 9 грн коштує зошит.
Завдання 1248
За 2 год пішки і 1 год на велосипеді туристка подолала 18 км, а за 1 год пішки і 2 год на велосипеді – 27 км. З якою швидкістю туристка рухалася пішки і з якою – на велосипеді?
Розв'язання
Нехай туристка пішки рухалася зі швидкістю x км/год, а на велосипеді — y км/год. За 2 год пішки подолала 2х км, а за 2 год на велосипеді — 2у км. Складаємо систему рівнянь:
{2x + y = 18 |•(–2)
x + 2y = 27
{–4x – 2y = –36
x + 2y = 27
–3x = –9
х = (–9) : (–3)
x = 3
Підставимо знайдене значення х у рівняння х + 2у = 27:
3 + 2у = 27
2у = 24
у = 12
Відповідь: швидкість пішки 3 км/год і швидкість на велосипеді 12 км/год.
Завдання 1249
У касі крамниці після переобліку залишилося 12 монет по 50 к. і по 1 грн, усього на суму 8 грн. Скільки монет по 50 к. і скільки по 1 грн залишилося в касі?
Розв'язання
Нехай у касі x монет по 50 к., загальна вартість яких 0,5х грн, і y монет по 1 грн, загальна вартість яких у грн. Складаємо систему рівнянь:
{x + y = 12
0,5x + y = 8 |•(–2)
{x + y = 12
–x – 2y = –16
–y = –4
у = (–4) : (–1)
y = 4
Підставимо знайдене значення у в рівняння х + у = 12:
х + 4 = 12
х = 8
Відповідь: 8 монет по 50 к. і 4 монети по 1 грн.
Завдання 1250
Було придбано 16 зошитів у клітинку і лінійку, усього на суму 328 грн. Зошит у клітинку коштує 22 грн, а в лінійку – 18 грн. Скільки зошитів у клітинку і скільки зошитів у лінійку було придбано?
Розв'язання
Нехай у клітинку придбали x зошитів, а в лінійку — у зошитів. За зошити в клітинку заплатили 22х грн, а за зошити в лінійку — 18у грн. Складаємо систему рівнянь:
{x + y = 16 |•(–22)
22x + 18y = 328
{–22x – 22y = –352
22x + 18y = 328
–4y = –24
у = (–24) : (–4)
y = 6
Підставимо знайдене значення у в рівняння х + у = 16:
x + 6 = 16
х = 10
Відповідь: 10 зошитів у клітинку і 6 зошитів у лінійку.
Завдання 1251
За 3 футбольних і 2 волейбольних м'ячі заплатили 1088 грн. Скільки коштує футбольний м'яч і скільки волейбольний, якщо два волейбольних м'ячі на 192 грн дорожчі за один футбольний?
Розв'язання
Нехай футбольний м’яч коштує x грн, а волейбольний — у грн. Тоді 3 футбольних м'ячі коштують 3х грн, а 2 волейбольні — 2у грн Складаємо систему рівнянь:
{3x + 2y = 1088
2y – x = 192 |•3
{3x + 2y = 1088
–3x + 6y = 576
8y = 1664
y = 208
Підставимо знайдене значення у в рівняння 2у - х = 192:
2 • 208 – х = 192
416 – х = 192
х = 224
Відповідь: футбольний м’яч коштує 224 грн, а волейбольний м'яч — 208 грн.
Завдання 1252
2 акумулятори і 3 батарейки разом коштують 252 грн. Скільки коштує один акумулятор і скільки одна батарейка, якщо акумулятор коштує стільки само, скільки 3 батарейки?
Розв'язання
Нехай один акумулятор коштує x грн, а одна батарея — у грн. За два акумулятори заплатили 2х грн, а за 3 батарейки — 3у грн. Складаємо систему рівнянь і розв'язуємо її:
{2x + 3y = 252
x = 3y
Підставимо змінну х в перше рівняння системи, одержимо рівняння:
2 • 3y + 3y = 252
9y = 252
y = 28
Підставимо знайдене значення у в рівняння х = 3у:
x = 3 • 28
х = 84
Відповідь: акумулятор коштує 84 грн, а батарейка — 28 грн.
Завдання 1253
Основа рівнобедреного трикутника на 2 см більша за його бічну сторону. Знайдіть сторони трикутника, якщо його периметр дорівнює 26 см.
Розв'язання
Нехай бічна сторона рівнобедреного трикутника дорівнює x см, а основа — y см. Основа на 2 см більша за бічну сторону, тобто у – х = 2 см, а периметр дорівнює 26, тобто у + 2х = 26 см. Складаємо систему рівнянь:
{y – x = 2 |•2
у + 2х = 26
{2y – 2x = 4
у + 2х = 26
3у = 30
у = 30 : 3
у = 10
Підставимо знайдене значення у в рівняння у - х = 2:
10 – х = 2
х = 8
Відповідь: основа рівнобедреного трикутника дорівнює 10 см, а бічна сторона — 8 см.
Завдання 1254
Довжина прямокутника на 8 м більша за ширину. Знайдіть довжину і ширину прямокутника, якщо його периметр дорівнює 56 м.
Розв'язання
Нехай довжина прямокутника x м, а ширина — у м. Довжина на 8 м більша за ширину, тобто х – у = 8 м, а периметр прямокутника дорівнює 56 м, тобто 2(х + у) = 56 м. Складаємо систему рівнянь:
{2(x + y) = 56 |:2
x – y = 8
{x + y = 28
x – y = 8
2x = 36
x = 18
Підставимо знайдене значення х у рівняння х - у = 8:
18 – y = 8
у = 10
Відповідь: довжина прямокутника дорівнює 18 м, а ширина — 10 м.
Завдання 1255
Човен за 3 год руху за течією і 2 год руху проти течії долає 92 км. За 9 год руху за течією човен долає відстань у 5 разів більшу, ніж за 2 год руху озером. Знайдіть власну швидкість човна та швидкість течії.
Розв'язання
Нехай власна швидкість човна х км/год, а швидкість течії у км/год, тоді швидкість за течією (х + y) км/год, а швидкість проти течії — (х – у) км/год. За 3 год за течією річки човен пройде 3(х + у) км, а за 2 год проти течії — 2(х – у) км, що разом дорівнює 92 км, тобто 3(х + у) + 2(х – у) = 92 км. За 9 год за течією річки долає відстань 9(х + у) км, а за 2 год озером — 2х км, що у 5 разів більшою є, тобто 5•2х = 10х км. Складаємо систему рівнянь:
{3(x + y) + 2(x – y) = 92
9(x + y) = 10x
{3x + 3y + 2x – 2y = 92
9x + 9y = 10x
{5x + y = 92 |•9
х – 9у = 0
{45x + 9y = 828
х – 9у = 0
46х = 828
х = 828 : 46
х = 18
Підставимо знайдене значення х у рівняння х - 9у = 0:
18 – 9у = 0
9у = 18
у = 2
Відповідь: швидкість човна 8 км/год, швидкість течії 2 км/год.
Завдання 1256
Човен рухався 2 год за течією і 5 год проти течії, подолавши за цей час 110 км. Швидкість човна проти течії становить 70 % від швидкості човна за течією. Знайдіть власну швидкість човна та швидкість течії.
Розв'язання
Нехай власна швидкість човна у км/год, а швидкість течії х км/год, тоді швидкість човна за течією становить (х + у) км/год, а проти течії — (у – х) км/год. Човен за 2 год за течією подолав 2(х + у) км, а за 5 год проти течії — 5(у – х) км, що разом дорівнює 110 км, тобто 2(х + у) + 5(у – х) = 110 км. Складаємо систему рівнянь:
{2(x + y) + 5(y – x) = 110
у – х = 7/10 • (х + у) |•10
{2х + 2у + 5у – 5х = 110
10у – 10х = 7(х + у)
{7у – 3х = 110
10у – 10х = 7х + 7у
{7у – 3х = 110
3у = 17х
З другого рівняння системи виразимо змінну у через х, одержимо:
y = 17/3 x
Підставимо значення у в перше рівняння системи, одержимо рівняння:
7 • (17/3 x) – 3x = 110
119/3 x – 3x = 110 |•3
119x – 9x = 330
110x = 330
x = 3
Підставимо знайдене значення х у рівняння у = 17/3 х:
y = 17/3 • 3
у = 17
Відповідь: швидкість човна 17 км/год і швидкість течії річки 3 км/год.
Завдання 1257
З пунктів A і B, відстань між якими 168 км, одночасно вирушають велосипедистка і мотоцикліст. Якщо вони будуть рухатися назустріч одне одному, то зустрінуться через 3 год. А якщо рухатимуться в одному напрямку, то мотоцикліст наздожене велосипедистку через 6 год. Знайдіть швидкість кожного з них.
Розв'язання
Нехай швидкість велосипедистки x км/год, а мотоцикліста — y км/год. За 3 год назустріч вони подолають відстань 168 км, тобто 3х + 3у = 168 км. Якщо рухатимуться в одному напрямку, то мотоцикліст наздожене велосипедистку за 6 год, тобто а 6у - 8х = 168 км. Складаємо систему рівнянь:
{3x + 3y = 168
6y – 6x = 168 |:2
{3x + 3y = 168
–3x + 3y = 84
6y = 252
у = 252 : 6
y = 42
Підставимо знайдене значення у в рівняння 3х+ 3у = 168:
3х + 3 • 42 = 168
3х + 126 = 168
3х = 42
х = 14
Відповідь: швидкість велосипедистки 14 км/год, а мотоцикліста — 42 км/год.
Завдання 1258
Сума двох чисел дорівнює 62. Знайдіть кожне із чисел, якщо 70 % від одного і 60 % від другого разом становлять 39,6.
Розв'язання
Нехай перше число дорівнює x, а друге число — у, а їхня сума 62, тобто х + у = 62. 70% від першого числа дорівнює 0,7х, а 60% від другого — 0,6у, а їхня сума 39,6, тобто 0,7х + 0,6у = 39,6. Складаємо систему рівнянь:
{x + y = 62 |•(–7)
0,7x + 0,6y = 39,6 |•10
{–7x – 7y = –434
7x + 6y = 396
–y = –38
у = (–38) : (–1)
y = 38
Підставимо знайдене значення у в рівняння х + у = 62:
x + 38 = 62
х = 24
Відповідь: перше число 24, друге число 38.
Завдання 1259
20% від одного числа на 2,4 більше за 10% від другого. Знайдіть ці числа, якщо їх сума дорівнює 72.
Розв'язання
Нехай перше число дорівнює x, а друге число — у, а їхня сума дорівнює 72, тобто х + у = 72. 20% від першого числа дорівнює 0,2х, а 10% від другого — 0,1у, а їх різниця 2,4, тобто 0,2х - 0,1у = 2,4. Складаємо систему рівнянь:
{x + y = 72
0,2x – 0,1y = 2,4 |:0,1
{x + y = 72
2x – y = 24
3x = 96
х = 96 : 3
x = 32
Підставимо знайдене значення х у рівняння х + у = 72:
32 + y = 72
у = 40
Відповідь: перше число 32, друге число 40.
Завдання 1260
Матері разом з донькою 42 роки. Через рік мати стане втричі старшою за доньку. Скільки років кожній з них зараз?
Розв'язання
Нехай зараз матері x років, а доньці у років, а разом їм 42 роки, тобто х + у = 42. Через рік матері стане (х + 1) років, а доньці — (у + 1) років, причому мати стане старшою від доньки утричі, тобто (х + 1) = 3(у + 1). Складаємо систему рівнянь:
{x + y = 42
x + 1 = 3(y + 1)
{x + y = 42
x + 1 = 3y + 3
{x + y = 42 |•(–1)
x – 3y = 2
{–x – y = –42
x – 3y = 2
–4y = –40
у = (–40) : (–4)
y = 10
Підставимо знайдене значення у в рівняння х + у = 42:
х + 10 = 42
х = 42 – 10
х = 32
Відповідь: матері 32 роки, доньці 10 років.
Завдання 1261
Розв'яжіть систему рівнянь. Складіть задачу, яка б розв'язувалася за допомогою цієї системи.
1) {x + y = 17
x – y = 5
2x = 22
х = 22 : 2
x = 11
Підставимо знайдене значення х у рівняння х + у = 17:
11 + y = 17
у = 6
Відповідь: (11;6)
Знайдіть числа, сума яких дорівнює 17, а їхня різниця дорівнює 5.
2) {2x + 3y = 15
x – y = 1
З другого рівняння системи виразимо змінну х через у, одержимо:
x = 1 + y
Підставимо значення х в перше рівняння системи, одержимо рівняння:
2(1 + y) + 3y = 15
2 + 2y + 3y = 15
5y = 13
у = 13 : 5
y = 2,6
Підставимо знайдене значення у в рівняння х - у = 1:
x – 2,6 = 1
х = 3,6
Відповідь: (3,6;2,6)
Учень купив 2 ручки і 3 олівці за 15 грн. Скільки коштують окремо ручка й олівець, якщо ручка дорожча від олівця на 1 грн.
Завдання 1262
1) {x – y = 8
x + y = 12
2x = 20
х = 20 : 2
x = 10
Підставимо знайдене значення х у рівняння х - у = 8:
10 – у = 8
y = 10 – 8
у = 2
Відповідь: (10;2)
Знайдіть числа, сума яких дорівнює 12, а їхня різниця дорівнює 8.
2) {2x + y = 18
3x – y = 2
5x = 20
х = 20 : 5
x = 4
Підставимо знайдене значення х у рівняння 2х + у = 18:
2 • 4 + у = 18
8 + у = 18
у = 10
Відповідь: (4;10)
Учень купив 2 ручки і 1 зошит за 18 грн. Скільки коштують окремо ручка й зошит, якщо три ручки дорожчі від зошита на 2 грн.
Завдання 1263
У ящику і кошику разом 95 яблук. Якщо кількість яблук у ящику зменшити вдвічі, а кількість яблук у кошику збільшити на 25, то яблук у ящику і кошику стане порівну. Скільки яблук у ящику і скільки – в кошику?
Розв'язання
Нехай спочатку в ящику було х яблук, а в кошику — у яблук, а разом 95 яблук, тобто х + у = 95. У ящику зменшили яблук вдвічі, тобто х/2, а в кошику збільшили на 25, тобто (у + 25) яблук, після чого їх стало порівнр, тобто х/2 = у + 25. Складаємо систему рівнянь:
{x + y = 95
x/2 = y + 25 |•(–2)
{x + y = 95
–x + 2y = –50
3y = 45
у = 45 : 3
y = 15
Підставимо знайдене значення у в рівняння х + у = 95:
х + 15 = 95
х = 95 – 15
х = 80
Відповідь: 80 яблук у ящику і 15 яблук у кошику.
Завдання 1264
Сума двох чисел дорівнює 45. Знайдіть ці числа, якщо 60 % від першого з них дорівнюють 75 % від другого.
Розв'язання
Нехай перше число дорівнює x, а друге число — у, а їхня сума 45, тобто х + у = 45. 60% від першого дорівнює 06х, а 75% від другого — 0,75у, причому числа рівні, тобто 0,6х = 0,75у. Складаємо систему рівнянь:
{x + y = 45
0,6x = 0,75y
З першого рівняння системи виразимо змінну х через у, одержимо:
x = 45 – y
Підставимо значення х в друге рівняння системи, одержимо рівняння:
0,6(45 – y) = 0,75y
27 – 0,6y = 0,75y
–1,35y = –27
у = (–27) : (–1,35)
y = 20
Підставимо знайдене значення у в рівняння х + 20 = 45:
x + 20 = 45
х = 45 – 20
х = 25
Відповідь: перше число 25, друге число 20.
Завдання 1265
Знайдіть два числа, якщо їх сума дорівнює 200 і 11/24 від одного з них дорівнюють 3/8 від другого.
Розв'язання
Нехай перше число дорівнює x, а друге число — у, а їхня сума дорівнює 200, тобто х + у = 200. 11/24 від першого числа дорівнює 11/24 х, а 3/8 від другого числа — 3/8 у, причому вони рівні, тобто 11/24 х = 308 у. Складаємо систему рівнянь:
{x + y = 200
11/24x = 3/8y |•24
{x + y = 200
11x = 9y
З першого рівняння системи виразимо змінну х через у, одержимо:
x = 200 – y
Підставимо значення х в друге рівняння системи, одержимо рівняння:
11(200 – y) = 9y
2200 – 11y = 9y
20y = 2200
у = 2200 : 11
y = 110
Підставимо знайдене значення у в рівняння х + у = 200:
x + 110 = 200
х = 90
Відповідь: перше число дорівнює 90, друге число дорівнює 110.
Завдання 1266
Змішали два види цукерок вартістю 60 грн і 75 грн за кілограм. Після чого утворилося 20 кг суміші вартістю 66 грн за кілограм. По скільки кілограмів цукерок кожного виду взяли для суміші?
Розв'язання
Нехай цукерок вартістю 60 грн взяли x кг, а цукерок вартістю 75 грн — y кг, одержали 20 кг суміші, тобто х + у = 20 кг. Цукерки масою х кг коштують 60х грн, а масою у кг — 75 грн, за які заплатили 20 • 66 = 1320 грн. Складаємо систему рівнянь:
{x + y = 20 |•(–75)
60x + 75y = 1320
{–75x – 75y = –1500
60x + 75y = 1320
–15x = –180
х = (–180) : (–15)
х = 12
Підставимо знайдене значення х у рівняння х + у = 20:
12 + у = 20
у = 8
Відповідь: 12 кг цукерок по 60 грн і 8 кг цукерок по 75 грн.
Завдання 1267
З двох сортів печива вартістю 40 грн і 55 грн за кілограм утворили 25 кг суміші вартістю 49 грн за кілограм. По скільки кілограмів печива кожного виду взяли?
Розв'язання
Нехай печива вартістю 40 грн взяли x кг, а печива вартістю 55 грн — y кг, утворили 25 кг суміші, тобто х + у = 25 кг. Печиво масою х кг коштує 60х грн, а масою у кг — 55 грн, за які заплатили 25 • 49 = 1225 грн Складаємо систему рівнянь:
{x + y = 25 |•(–55)
40x + 55y = 1225
{–55x – 55y = –1375
40x + 55y = 1225
–15х = –150
х = –150 : (–15)
х = 10
Підставимо знайдене значення х у рівняння х + у = 25:
10 + у = 25
y = 25 – 10
у = 15
Відповідь: 10 кг печива по 40 грн і 15 кг печива по 55 грн.
Завдання 1268
У двох бідонах разом було 75 л олії. Після того як половину олії з першого бідона перелили в другий, там олії стало в 4 рази більше, ніж у першому. По скільки літрів олії було в кожному бідоні спочатку?
Розв'язання
Нехай олії у першому бідоні було x л, а в другому бідоні — у л. Після переливання у першому бідоні залишилося (х – 0,5x) = 0,5х л олії, а у другому стало (y + 0,5x) л олії. Складаємо систему рівнянь:
{x + y = 75
4 • 0,5x = y + 0,5x
{x + y = 75
1,5x = y
Підставимо змінну у в перше рівняння системи, одержимо рівняння:
х + 1,5х = 75
2,5x = 75
х = 75 : 2,5
x = 30
Підставимо знайдене значення х у рівняння х + у = 75:
30 + y = 75
у = 75 – 30
у = 45
Відповідь: у першому бідоні було 30 л олії, а у другому — 45 л олії.
Завдання 1269
На двох полицях разом 57 книжок. Після того як з першої полиці переставили 5 книжок на другу, там їх стало вдвічі більше, ніж на першій. По скільки книжок було на кожній полиці спочатку?
Розв'язання
Нехай на першій полиці було книжок, а на другій — у книжок, а разом на двох полицях 57 книжок, тобто х + у = 57. Після переставлення на першій полиці залишилося (x – 5) книжок, а на другій стало (y + 5) книжок, що вдвічі більше, ніж на першій. Складаємо систему рівнянь:
{x + y = 57
2(x – 5) = (y + 5)
{x + y = 57
2x – 10 = y + 5
{x + y = 57
2x – у = 15
3x = 72
х = 72 : 3
x = 24
Підставимо знайдене значення х у рівняння х + у = 57:
24 + у = 57
y = 57 – 24
у = 33
Відповідь: на першій полиці 24 книжки, на другій полиці 33 книжки.
Завдання 1270
За 5 світильників і 4 ліхтарики заплатили 896 грн. Після того як світильники подешевшали на 15 %, а ліхтарики подорожчали на 10 %, один світильник і один ліхтарик разом стали коштувати 196 грн. Якою була початкова вартість світильника і якою – ліхтарика?
Розв'язання
Нехай спочатку світильник коштував х грн, а ліхтарик — у грн, тоді за 5 світильників заплатили 5х грн, за 4 ліхтарики — 4у грн, а їхня загальна вартість 896 грн, тобто 5х + 4у = 896 грн. Світильники після подешевшення на 15% коштуватимуть 0,85х грн, ліхтарики після подорожчання на 10% — 1,1у грн, а їхня загальна вартість 196 грн. Складаємо систему рівнянь:
{5x + 4y = 896
0,85x + 1,1y = 196
З першого рівняння системи виразимо змінну х через у, одержимо:
x = (896 – 4y)/5
Підставимо змінну х в перше рівняння системи, одержимо рівняння:
0,85(896 – 4y)/5 + 1,1y = 196
0,17(896 – 4y) + 1,1y = 196
152,32 – 0,68x + 1,1y = 196
0,42y = 43,68
у = 43,68 : 0,42
y = 104
Підставимо знайдене значення у в рівняння х = (896 - 4у)/5:
x = (896 – 4 • 104)/5 = (896 – 416)/5 = 96
Відповідь: спочатку коштували світильник 96 грн і ліхтарик 104 грн.
Завдання 1271
Два кондитерських цехи за день мали разом виготовити 300 тортів. Коли перший цех виконав 55% свого завдання, а другий – 60% свого, виявилося, що перший цех виготовив на 27 тортів більше, ніж другий. По скільки тортів мав виготовити кожен цех?
Розв'язання
Нехай за планом перший цех мав виготовити x тортів, а другий — у тортів, разом 300 тортів, тобто х + у = 300. Перший цех виконав 55% свого завдання, тобто виготовив 0,55х тортів, другий — 60% свого завдання, тобто 0,6у тортів, різниця яких складає 27 тортів. Складаємо систему рівнянь:
{x + y = 300 |•0,6
0,55 – 0,6y = 27
{0,6x + 0,6y = 180
0,55 – 0,6y = 27
1,15x = 207
х = 207 : 1,15
x = 180
Підставимо знайдене значення х у рівняння х + у = 300:
180 + у = 300
y = 300 – 180
у = 120
Відповідь: мали виготовити перший цех 180 тортів і другий цех 120 тортів.
Завдання 1272
Якщо чисельник даного дробу збільшити на 7, то дріб дорівнюватиме 2/3. Якщо знаменник даного дробу збільшити на 2, то дріб дорівнюватиме 0,25 (1/4). Знайдіть цей дріб.
|
|
Був |
Став |
Став |
|
Чисельник |
x |
x + 7 |
x |
|
Знаменник |
y |
y |
y + 2 |
|
Дріб |
x/y |
(x + 7)/y = 2/3 |
x/(y + 2) = 1/4 |
Розв'язання
{(x + 7)/y = 2/3
x/(y + 2) = 1/4
{3х + 21 = 2у
4х = у + 2
{3х – 2у = –21
4х – у = 2 |•(–2)
{3х – 2у = –21
–8x + 2y = –4
Додамо почленно рівняння системи, одержимо рівняння:
–5х = –25
х = (–25) : (–5)
x = 5
Підставимо знайдене значення х у рівняння 4х - у = 2:
4 • 5 – у = 2
20 – у = 2
у = 18
Відповідь: 5/18.
Завдання 1273
Якщо чисельник дробу зменшити на 2, то дріб дорівнюватиме 0,5. Натомість, якщо знаменник дробу збільшити на 11, то дріб дорівнюватиме 1/3. Знайдіть цей дріб.
|
|
Був |
Став |
Став |
|
Чисельник |
x |
x – 2 |
x |
|
Знаменник |
y |
y |
y + 11 |
|
Дріб |
x/y |
(x – 1)/y = 1/2 |
x/(y + 11) = 1/3 |
Розв'язання
{(x – 2)/y = 1/2
x/(y + 11) = 1/3
{2x – 4 = y
3x = y + 11
{2x – y = 4
3x – y = 11
{–2x + y = –4 |•(–1)
3x – y = 11
x = 7
Підставимо знайдене значення х у рівняння 2х - у = 4:
2 • 7 – у = 4
14 – у = 4
у = 10
Відповідь: 7/10.
Завдання 1274
Скільки грамів кожного з 2–відсоткового і 6–відсоткового розчинів солі потрібно взяти, щоб отримати 200 г 5–відсоткового розчину?
Розв'язання
Нехай маса 2%-го розчину х г, а 6%-го — у г, а загальна маса 200 г, тобто х + у = 200. Солі в 2%-му розчині було 0,02х г, в 6%-му розчині — 0,06y г. Складаємо систему рівнянь:
{х + у = 200
0,02х + 0,06у = 200 • 0,05
{х + у = 200 |•(–0,06)
0,02х + 0,06у = 10
{–0,06х – 0,06у = –12
0,02х + 0,06у = 10
–0,04х = –2
х = (–2) : (–0,04)
х = 50
Підставимо знайдене значення х у рівняння х + у = 200:
50 + у = 200
у = 200 – 50
у = 150
Відповідь: 50 г 2–відсоткового розчину солі і 150 г 6–відсоткового розчину солі.
Завдання 1275
В одному сплаві міститься 9% цинку, а в другому – 24%. По скільки грамів кожного сплаву потрібно взяти, щоб одержати зливок масою 260 г, що містить 15 % цинку?
Розв'язання
Нехай маса 9%-го сплаву x г, а маса 24%-го сплаву у г. Цинку в 9%-вому сплаві було 0,09х г, а в 24%-вому — 0,24у г. Складаємо систему рівнянь:
{x + y = 260
0,09x + 0,24y = 0,15 • 260
{x + y = 260 |•(–0,24)
0,09x + 0,24y = 39
{–0,24x – 0,24y = –62,4
0,09x + 0,24y = 39
–0,15x = –23,4
х = (–23,4) : (–0,15)
x = 156
Підставимо знайдене значення х у рівняння х + у = 260:
156 + у = 260
y = 260 – 156
у = 104
Відповідь: треба взяти 156 г 9%-го сплаву і 104 г 24%-го сплаву.
Завдання 1276
Чотири роки тому батько був у 8 разів старший за сина, а через 20 років батько стане вдвічі старший за сина. Скільки років кожному з них зараз?
Розв'язання
Нехай зараз батькові х років, а синові — у років. Чотири роки тому батькові було (х - 4) роки, а синові — (у - 4) років, причому батько був у 8 разів старший, тобто х - 4 = 8(х - 4). Через 20 років батькові буде (х - 20) років, а синові — (у - 20) років, причому батько стане удвічі старший, тобто х + 20 = 2(у + 20). Складаємо систему рівнянь:
{x – 4 = 8(y – 4)
х + 20 = 2(y + 20)
{х – 4 = 8у – 32
х + 20 = 2у + 40
{x – 8y = –28 |•(–1)
x – 2y = 20
{–x + 8y = 28
x – 2y = 20
6y = 48
у = 48 : 6
y = 8
Підставимо знайдене значення у в рівняння х - 2у = 20:
x – 2 • 8 = 20
х – 16 = 20
х = 36
Відповідь: зараз 36 років батькові і 8 років синові.
Завдання 1277
Якщо суму цифр двоцифрового числа збільшити в 5 разів, то вона дорівнюватиме самому числу. А якщо його цифри поміняти місцями, то воно збільшиться на 9. Знайдіть це число.
Нехай у двоцифровому числі ху = 10х + у, цифра десятків дорівнює x, а цифра одиниць — у. Збільшена в 5 разів сума цифр 5(х + у) двоцифрового числа дорівнює даному числу, тобто 5(х + у) = 10х + у. Якщо суму цифр даного числа поміняти місцями, то отримаємо число 10у + х, яке збільшиться на 9 в порівнянні з даним, тобто 10у + х = 10х + у + 9. Складаємо систему рівнянь:
{5(x + y) = 10x + y
10у + х = 10х + у + 9
{5x + 5y = 10x + y
10у + х = 10х + у + 9
{5x + 5y – 10х – у = 0
10у + х – 10х – у = 9
{–5x + 4y = 0
–9х + 9y = 9 |:9
{–5x + 4y = 0
–х + y = 1 |(–5)
{–5x + 4y = 0
5x – 5y = –5
–y = –5
у = (–5) : (–1)
y = 5
Підставимо знайдене значення у в рівняння -х + у = 1:
–х + 5 = 1
–х = –4
х = –4 : (–1)
x = 4
Відповідь: двоцифрове число 45.
Завдання 1278 Розклад на множники многочлена
|
1) m² + 10m + 25 = (m + 5)² 3) р² – 0,36 = (р – 0,6)(p + 0,6) |
2) с² – 8с + 16 = (с – 4)² 4) –49а² + b² = b²– 49а² = (b – 7a)(b + 7а) |
Завдання 1279 Спрощення виразу
1) 2х(3х – 4x3) – (х + Зх²)² = 6х² – 8х4 – x² – 6х3 – 9х4 = 5x² – 17х4 – 6х3
2) 2р²(2р² – 6pm) – (2p² – Зmр)² = 4р4 – 12р3m – 4р4 + 12р3m – 9m²р² = – 9m²р²
Завдання 1280
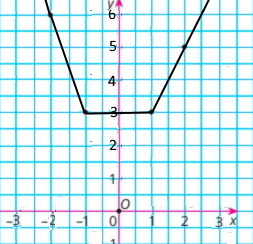
Побудуйте графік функції:
у = {–Зх, якщо x < –1;
З, якщо –1 ≤ х ≤ 1,
2х + 1, якщо х > 1
Завдання 1281
Діти 11–15 років на кожний кілограм своєї маси мають щоденно вживати 2,6 г білків, 2,3 г жирів, 10,4 г вуглеводів. Дізнайтеся власну масу тіла та визначте, скільки жирів, білків і вуглеводів маєте щоденно вживати ви.
Розв'язання
Припустимо, що маса дитини 45 кг.
(2,6 + 2,3 + 10,4) • 45 = 15,3 • 45 = 688,5 г
Відповідь: 688,5 г.
Завдання 1282
Задача Ньютона. Трава на галявині росте рівномірно щільно й швидко. Відомо, що 70 корів з'їли би її за 24 дні, а 30 корів – за 60 днів. Скільки корів з'їли би всю траву за 96 днів?
Траву, яку можуть з’їсти m корів за один день, одна корова може з’їсти за m днів.
Тому траву, яку з’їли 70 корів за 24 дні, одна корова з’їсть за 70 • 24 = 1680 днів, а ту
траву, яку 30 корів з’їдають за 60 днів, вистачить одній корові на 30 • 60 = 1800 днів.
Оскільки трава росте рівномірно, то за 60 – 24 = 36 днів виросте стільки трави, що
вистачить одній корові на 1800 – 1680 = 120 днів. Отже, ту кількість трави, яку одна
корова з’їдає за 1800 + 120 = 1920 днів, за 60 + 36 = 96 днів можуть з’їсти
1920 : 96 = 20 корів.
Відповідь: 20 корів.