графік функції х + у = 6	графік функції x – y = 4
1) (5;1); Належить, бо 5 + 1 = 6 2) (4;–2); Не належить, бо 4 – 2 = 2 3) (1;6) Не належить, бо 1 + 6 = 7 4) (6;0) Належить, бо 6 + 0 = 6	A(4;0); Належить, бо 4 – 0 = 4 B(1;3); Не належить, бо 1 – 3 = –2 С(3;–1); Належить, бо 3 + 1 = 4 D(0;4); Не належить, бо 0 – 4 = –4 E(5;1); Належить, бо 5 – 1 = 4

Завдання 1136

Чи проходить графік функції 7x + 5y = 25 через точку:

1) (7;–4); Не проходить, бо 7 • 7 + 5 • (–4) = 49 – 20 = 29

2) (5;–2); Проходить, бо 7 • 5 + 5 • (–2) = 25

3) (–1,4;7); Не проходить, бо 7 • (–1,4) + 5 • 7 = –9,8 + 35 = 25,2

4) (35;–44)? Проходить, бо 7 • 35 + 5 • (–44) = 245 – 220 = 25

 

Завдання 1137

Графіки яких рівнянь проходять через точку Р(–2;3):

1) 7x + 9y = 15; Не проходить, бо 7 • (–2) + 9 • 3 = –14 + 27 = 13

2) 17y – 4x = 59; Не проходить, бо 4 • (–2) – 17 • 3 = –8 – 51 = –59

3) 0x + 5y = 15; Проходить, бо 0 • (–2) + 5 • 3 = 0 + 15 = 15

4) 1/2x + 1/6y = –1; Не проходить, бо 1/2 • (–2) + 1/6 • 3 = –1 + 1/2 = –0,5

5) 0x + 0y = 5; Не проходить, бо 0 • (–2) + 0 • 3 = 0

6) 1,7x + 1,2y = 0,2? Проходить, бо 1,7 • (–2) + 1,2 • 3 = –3,4 + 3,6 = 0,2

 

Завдання 1138

Доведіть, що графіки рівнянь 5x – 8y = –66, 0x + 3y = 21 та 7y – 4x = 57 проходять через точку M(–2;7).

Графік рівняння 5х – 8y = –66 проходить через точку М(–2;7), бо

5 • (–2) – 8 • 7 = –10 – 56 = –66.

Графік рівняння 0x + 3y = 21 проходить через точку М(–2;7), бо

0 • (–2) + 3 • 7 = 21.

Графік рівняння –4x + 7у = 57 проходить через точку М(–2;7), бо

–4 • (–2) + 7 • 7 = 8 + 49 = 57.

Отже, графіки рівнянь 5х – 8y = –66, 0x + 3y = 21, і –4х + 7y = 57 проходять через точку М(–2;7).

 

Завдання 1139

Назвіть дві довільні точки, які належать графіку рівняння 2x – 5y = 20.

Якщо х = 0, тоді 2 • 0 – 5y = 20; –5y = 20; у = –4, точка (0;–4)

Якщо х = 10, тоді 2 • 10 – 5y = 20; 20 – 5y = 20; у = 0, точка (10;0)

Графіку рівняння 2х – 5y = 20 належать точки (0;–4) і (10;0). 

 

Завдання 1140

Дві точки, які належать графіку рівняння 3x + 2y = 12, і дві точки, які йому не належать.

Якщо х = 0, тоді 3 • 0 + 2y = 12; 2y = 12; у = 6, точка (0;6)

Якщо х = 4, тоді 3 • 4 + 2y = 12; 12 + 2y = 12; у = 0, точка (4;0)

Графіку рівняння Зх + 2y = 12 належать точки (0;6) і (4;0), а не належать — (0;5) і (4;1).

 

Завдання 1141 Графіки

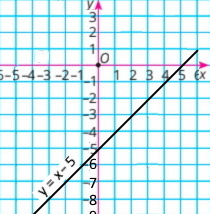
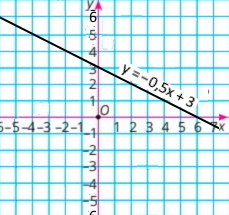
1) x – y = 5     у = x – 5 х 0 6 у –5 1	2) 0,5x + y = 3     у = –0,5х + 3 х 0  2 у 3  2
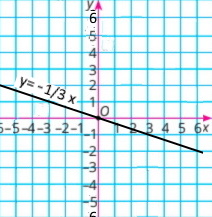
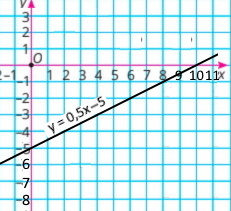
3) x + 3y = 0    3у = –х    у = –1/3 х х –3 3 у 1 –1	4) 0,2x – 0,4y = 2    0,4у = 0,2х – 2    у = 0,5х – 5 х 0 2 у –5 –4

Завдання 1142

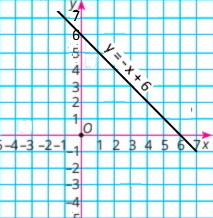
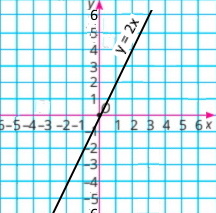
1) x + y = 6    у = –х + 6 х 0 1 у 6 5	2) y – 2x = 0     у = 2х х –1  1 у –2  2
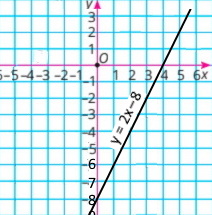
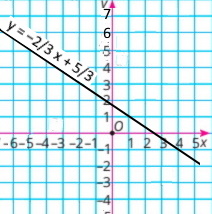
3) x – 0,5y = 4     0,5у = х – 4     у = 2х – 8 х 0  1 у –8 –6	4) 2x + 3y = 5     3у = 5 – 2х     у = (5–2х)/3 = -2/3 х + 5/3 х –2 7 у 3 3

Завдання 1143

Запишіть яке–небудь лінійне рівняння з двома змінними, графік якого проходить через точку Р(1;–3). 2х + 3у = –7, бо 2 • 1 + 3 • (–3) = –7

 

Завдання 1144

На графіку рівняння 2x + 3y = 7 вибрано точку з абсцисою –4. Знайдіть ординату цієї точки.

Якщо х = –4 , тоді 2 • (–4) + Зу = 7; –8 + Зу = 7; Зу = 15; у = 5

 

Завдання 1145

На графіку рівняння 5x – 7y = 16 взято точку з ординатою –2. Яка абсциса в цієї точки?

Якщо у = –2, тоді 5x – 7 • (–2) = 16; 5x + 14 = 16; 5x = 2; x = 0,4.

 

Завдання 1146 Графіки 

1) 0x + 2,5y = 12,5     2,5у = 12,5     у = 5	2) 7x + 0y = –14     7х = –14     х = –2
3) 1,9x = 5,7     х = 3	4) 3y = –7,5     у = –2,5

Завдання 1147 Графіки

1) 3x + 0y = –12     3x = –12     х = –4	2) 0x – 1,2y = 3,6     –1,2y = 3,6      у = –3
3) 1,8y = 7,2     у = 4	4) 4x = 6     х = 1,5

Завдання 1148

малюнок 26.6	малюнок 26.7	малюнок 26.8	малюнок 26.9
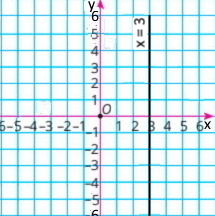
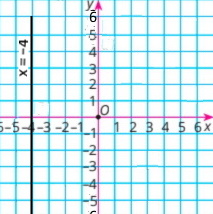
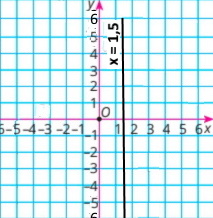
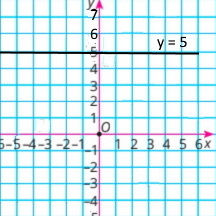
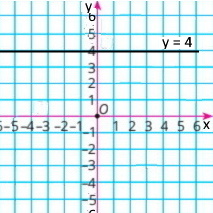
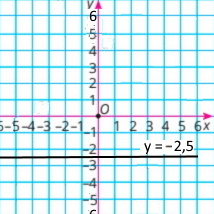
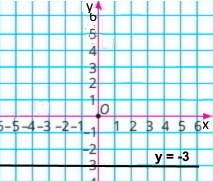
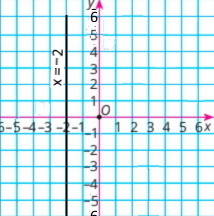
х = 2	у = 4	у = –3	х = –1

Завдання 1149

1) Графік рівняння 5х + 7у = m проходить через початок координат, тобто точка (0;0) належить графіку, то 0 + 0 = m; m = 0;

2) Графік рівняння mх + 2у = 14 проходить через точку (2;–3), то 2m – 6 = 14; 2m = 20; m = 10;

3) якщо графік рівняння 3х – 4у = m + 2 проходить через точку (–1;5), то

3 • (–1) – 4 • 5 = m + 2; –3 – 20 = m + 2; m = –3 – 20 – 2; m = –25.

 

Завдання 1150

Не виконуючи побудови, знайдіть координати точок перетину графіків рівнянь з осями координат:

1)  x + 7y = –21;

З віссю Ох (у = 0): х + 7 • 0 = –21; х = –21, тому в точці (–21;0)

З віссю Оу (х = 0): 0 + 7y = –21; 7у = –21; у = –3, тому в точці (0;–3)

2) 5x – 3y = 15.

З віссю Ох (у = 0): 5х – 3 • 0 = 15; 5х = 15; х = 3, тому в точці (3;0)

З віссю Оу (х = 0): 5 • 0 – Зу = 15; Зу = –15; у = –5, тому в точці (0;–5)

 

Завдання 1151

Не виконуючи побудови, знайдіть координати точок перетину графіків рівнянь з осями координат:

1) 3x + y = 18;

З віссю Ох (у = 0): Зх + 0 = 18; Зх = 18; х = 6, тому в точці (6;0)

З віссю Оу (х = 0): 3 • 0 + у = 18; у = 18, тому в точці (0; 18)

2) –7x – 2y = 28.

З віссю Ох (у = 0):: –7x – 2 • 0 = 28; –7x = 28; х = –4, тому в точці (–4;0).

З віссю Оу (х = 0): –7 • 0 – 2у = 28; –2у = 28; у = –14, тому в точці (0;–14).

 

Завдання 1152

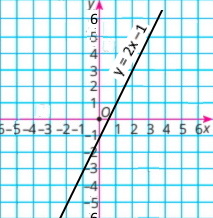
1) 2(x + y) – 3y = 1;    2х + 2у – 3y = 1    2х – y = 1    у = 2х – 1 х 0 1 у –1 1

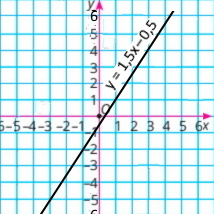
2) x/2 – y/3 = 1/6   |•6    3х –2у = 1    2у = 3х – 1     у = 1,5х – 0,5 х 0  3 у –0,5 4

Завдання 1153

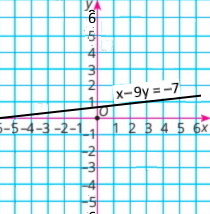
1) 5(x – y) – 4(x + y) = –7    5х – 5у – 4х – 4у = –7    х – 9y = –7    х = 9y –7 х –7 2 у 0 1

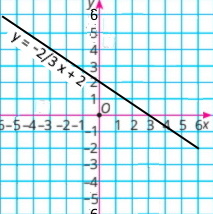
2) x/3 + y/2 = 1       у/2 = -х/3 + 1     |•6     3у = –2х + 6     у = –2/3 х + 2 х 0 3 у 2 0

Завдання 1154

Не виконуючи побудови, визначте, через які координатні кути проходить графік рівняння:

1) 2х – 6у = 0; 2x = 6у; х = Зу.

З рівності х = 3у випливає, що х і у набувають значень з однаковими знаками.

Отже, графік рівняння 2х – 6у = 0 розміщений у І і III координатних чвертях;

2) Зх + у = 0; у = –Зх.

З рівності у = –Зх слідує, що х і у набувають значень з протилежними знаками.

Отже, графік рівняння Зх +у = 0 розміщений у II і IV координатних чвертях;

3) 1,9х = 190; х = 100.

Графіком рівняння 1,9х = 190 є пряма, яка проходить через точку (100; 0) паралельно осі у і розміщена у І і IV координатних чвертях;

4) –8y = 720; у = –90.

Графіком рівняння –8у = 720 є пряма, яка проходить через точку (0; –90) паралельно осі х і розміщена у III і IV координатних чвертях.

 

Завдання 1155

Побудуйте в одній системі координат графіки рівнянь. 

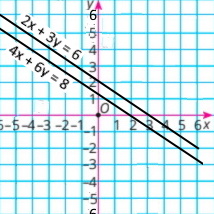
2x + 3y = 6	4x + 6y = 8
у = -2/3 х + 2 х 0 3 у 2 0	у = -2/3 х + 4/3 х –1 0 у 2 2

Ці графіки не перетинаються. вони паралельні. 

 

Завдання 1156

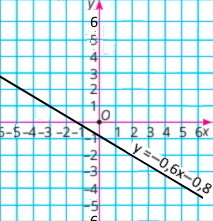
(x – 3)/5 + (y + 4)/3 = 7/15 |•15 3(x – 3) + 5(y + 4) = 7 3х – 9 + 5у + 20 = 7 3х + 5у = –4 5у = –3х – 4 у = – 0,6х – 0,8	х –3 2 у 1 –2

Завдання 1157

Пряму пропорційність задано формулою y = –1/4x.

1) Якщо х = –8 , то у = –1/4 • (–8) = 2     якщо х = 0, то у = –1/4 • 0 = 0     якщо x = 12, то у = –1/4 • 12 = –3     якщо x = 20, то y = –1/4 • 20 = –5

2) y = –2, якщо –2 = –1/4х; х = 8     у = 3, якщо 3 = –1/4х; х = –12     у = 10, якщо 10 = –1/4x; х = –40

Завдання 1158 Вираз у вигляді многочлена

1) 64а² – (8а – 1)² + 14а = 64а² – 64а² + 16а – 1 + 14а = 30а – 1;

2) m² + 4n² – (m + 2n)² – 12mn = m² + 4n² – m² – 4mn – 4n² – 12mn = –16mn;

3) 2m(m – 5) – (m – 5)² = 2m² – 10m – m² + 10m – 25 = m² – 25;

4) (х – 3)(х + 5) – (х + 1)² = х² + 5х – Зх – 15 – x² – 2х – 1 = –16.

 

Завдання 1159

Автомобіль та автобус одночасно виїхали назустріч один одному з пунктів A і B, відстань між якими 240 км. Швидкість автомобіля на 20 км/год більша за швидкість автобуса. Знайдіть швидкість автобуса та швидкість автомобіля, якщо вони зустрілися через 2 год після виїзду, при цьому автомобіль зробив на шляху півгодинну зупинку.

Розв'язання

Нехай швидкість автобуса х км/год, тоді швидкість автомобіля (х + 20) км/год. Відстань, яку проїхав автобус до зустрічі, дорівнює 2х км, а автомобіль — (x + 20)(2 – 0,5) = 1,5(х + 20) = (1,5x + 30) (км). Складаємо рівняння:

2x + 1,5x + 30 = 240

3,5x = 210

x = 60 (км/год) – швидкість автобуса;

60 + 20 = 80 (км/год) – швидкість автомобіля.

Відповідь: 60 км/год і 80 км/год.

 

Завдання 1160

Маса новонародженої дитини в середньому має становити 3 кг 300 г. Якщо батько дитини є курцем, то її маса буде на 125 г меншою від середньої, якщо ж курить мати – меншою на 300 г. Визначте, скільки відсотків маси втрачає дитина при народженні і округліть до цілих відсотків, якщо:

1) курить її батько;

3300 г — 100%

125 — х%

3300/125 = 100/х; 3300х = 12500; х = 3,79% ≈ 4% – маси втрачає дитина;

2) курить її мати.

3300 г — 100%

300 — х%

3300/300 = 100/х; 3300х = 30000; х = 9,09% ≈ 9% – маси втрачає дитина.

 

Завдання 1161

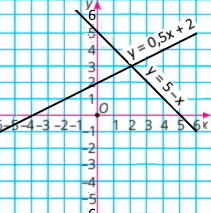
Побудуйте в одній системі координат графіки функцій y = 0,5x + 2 і y = 5 – x. За графіком знайдіть координати точки їх перетину.

y = 0,5x + 2 х 0 4 у 2 4	y = 5 – x х 0 4 у 5 1
Координати точки перетину (2;3)

Завдання 1162

Доведіть, що для будь–якого значення x значення виразу x⁸ – x⁵ + x² – x + 1 є числом додатним.

Розглянемо вираз x⁸ – x⁵ + x² – x + 1.

1) Якщо х ≤ 0, то х⁸ ≥ 0, x⁵ ≤ 0, тоді –x⁵ ≥ 0, x² ≥ 0, x ≤ 0, тоді –x ≥ 0,1 > 0.

Отже, x⁸+ (–x⁵) + x² + (–x)+ 1 > 0;

2) Якщо 0 < x ≤ 1, то 0 < xⁿ ≤ 1, тоді х⁸ – x⁵ + х² – x + 1 = х⁸ + x²(1 – х³) + (1 – x).

1 – x³ ≥ 0,1 – x ≥ 0, x⁸ > 0, x² >0, тому х⁸ – х⁵ + х² – х + 1 > 0;

3) якщо x > 1, то xⁿ > 1.

x⁸ – x⁵ + x² – x + 1 = x⁵(x³ – 1) + х( x – 1) + 1.

Отже, x⁵ > 1, x³ – 1 > 0, х > 0, х – 1 > 0, тому x⁸ – x⁵ + x² – х + 1 > 0.

Отже, x⁸ – x⁵ + x² – х + 1