Завдання 1283
Чи є пара чисел (7;1) розв'язком рівняння x – y = 6? Так, бо 7 – 1 = 6.
Знайдіть ще чотири розв'язки цього рівняння.
Пара чисел (9;3) є розв’язком рівняння, бо 9 – 3 = 6;
пара чисел (–1;–7) є розв’язком рівняння, бо –1 – (–7) = –1 + 7 = 6;
пара чисел (12 1/2; 6 1/2) є розв’язком рівняння x – у = 6, бо 12 1/2 – 6 1/2 = 6.
Завдання 1284
Знайдіть два будь–яких розв'язки рівняння:
1) 2x + y = 4;
Пара чисел (1;2), бо 2 • 1 + 2 = 2 + 2 = 4;
пара чисел (–1;6), бо 2 • (–1) + 6 = –2 + 6 = 4;
2) x – 3y = 7.
Пара чисел (1;–2), бо 1 – 3 • (–2) = 1 + 6 = 7;
пара чисел (28;7), бо 28 – 3 • 7 = 28 – 21 = 7.
Завдання 1285 Вираження змінної
1) y через змінну x з рівняння 7x – y = 18; у = 7x – 18
2) x через змінну y з рівняння 3x + 9y = 0; Зх = –9у, х = –Зу
3) y через змінну x з рівняння 13x – 2y = 6; 2у= 13х – 6; у = 6,5х – 3
4) x через змінну y з рівняння 8x + 15y = 24. 8x = 24 – 15у; х = 3 – 1,875х
Завдання 1286
Замініть «зірочки» числами так, щоб кожна з пар (*;3); (6;*); (*;–3); (15;*) була розв'язком рівняння x – 3y = 9.
Пара чисел (18;3) є розв’язком рівняння х – Зу = 9, бо 18 – 3 • 3 = 18 – 9 = 9;
пара чисел (3; –2) є розв’язком рівняння х – Зу = 9, бо: 3 – 3 • (–2)= 3 + 6 = 9;
пара чисел (0; –3) є розв’язком рівняння х – Зу = 9, бо: 0 – 3 • (–3) = 0 + 9 = 9;
пара чисел (15; 2) є розв’язком рівняння х – Зу = 9, бо: 15 – 3 • 2 = 15 – 6 = 9.
Завдання 1287
Доведіть, що рівняння з двома змінними не має розв'язків:
1) x² + y² =–4; Сума двох невід’ємних чисел не може дорівнювати від’ємному числу –4.
2) |x| + y² + 1 = 0; Сума невід’ємних чисел |x|, у² і додатного числа 1 не може дорівнювати нулю.
3) –|x| – |y| = 5; Недодатне число не може дорівнювати додатному числу.
4) 2x^4 + 3|y| = –2. Сума невід’ємних чисел не може дорівнювати від’ємному числу.
Завдання 1288
Знайдіть усі пари цілих чисел, які є розв'язками рівняння |x| + |y| = 2.
Якщо невід’ємні числа |x| і |у| є цілими і їхня сума дорівнює 2, то пара (|х|;|y|) може набувати значень: (0;2); (1;1); (2;0), тому розв’язками рівняння є пари чисел:
(0;2); (0;–2), (–1;1); (–1;–1); (1;1); (1;–1); (–2;0); (2;0).
До § 26
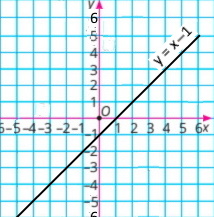
Завдання 1289 Побудова графіка
|
1) x – y = 1 у = x – 1
|
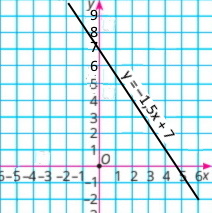
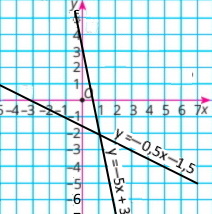
2) 1,5x + y = 7 у = –1,5х + 7
|
||||||||||||
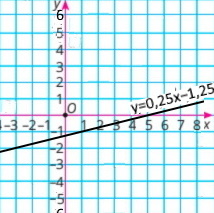
|
3) x – 4y = 5 у = 0,25х – 1,25
|
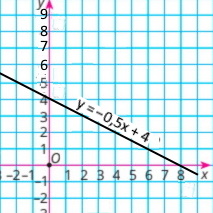
4) 0,1x + 0,2y = 0,8 у = –0,5х + 4
|
Завдання 1290
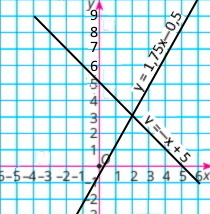
Побудуйте в одній координатній площині графіки рівнянь x + y = 5 і 7x – 4y = 2. Знайдіть координати точки їх перетину. Переконайтеся, що знайдена пара є розв'язком кожного з рівнянь.
|
x + y = 5 |
7x – 4y = 2 |
||||||||||||
|
у = –х + 5
|
у = 1,75х – 0,5
|
||||||||||||
|
Координати точки перетину (2:3) |
|||||||||||||
|
2 + 3 = 5 |
7 • 2 – 4 • 3 = 14 – 12 = 2 |
||||||||||||
Завдання 1291
Ордината деякої точки прямої, що є графіком рівняння –9x + 5y = 27, дорівнює нулю. Знайдіть абсцису цієї точки.
Якщо у = 0, то –9х = 27; х = –3
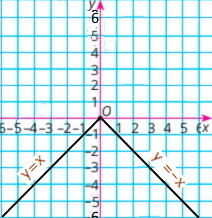
Завдання 1292 Побудова графіка рівняння, що містить модуль
|
1) |x| + y = 0 у = –|x| |
2) |x| + x – y = 0 у = |x| + x |
||||||||||||||||||||
|
Якщо х ≥ 0, то у = –х
|
Якщо х < 0, то у = –(–х) = х
|
Якщо х ≥ 0, то у = х + х = 2х
|
Якщо х < 0, то у = –х + х = 0 |
||||||||||||||||||
|
|
 |
||||||||||||||||||||
Завдання 1293
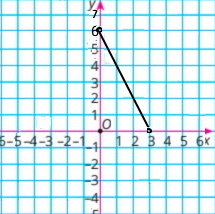
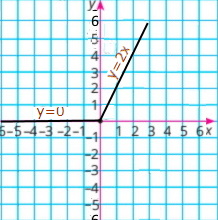
Побудуйте ту частину графіка рівняння 2x + y = 6, яка міститься в першій координатній чверті.
|
y = –2х + 6 |
|
|
До § 27
Завдання 1294
Чи є розв'язком системи рівнянь
{х – у = 0
х + у = 8
1) пара чисел: x = 5; y = 5; Ні, бо 5 – 5 = 0; 5 + 5 = 10, 10 ≠ 8;
2) пара чисел: x = 4; y = 4? Так, бо 4 – 4 = 0 в 4 + 4 = 8;
Завдання 1295 Графічне розв'язування системи рівнянь
|
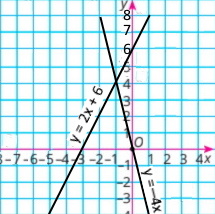
1) {у = –4х 2x – y = –6 |
2) {5х + у = З х + 2у = –3 |
||||||||||||||||||||||||||
|
у = –4x
|
y = 2х + 6
|
y = –5x + 3
|
y = –0,5х – 1,5
|
||||||||||||||||||||||||
|
Розв'язок (–1;4) |
Розв'язок (1;–2) |
||||||||||||||||||||||||||
Завдання 1296
|
1) {0х + 3у = 6 3x – 2y = 2 |
2) {7,1x = –14,2 2x + 7y = 17 |
||||||||||||||
|
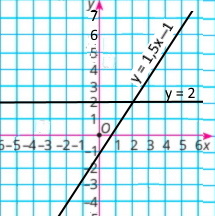
у = 2 |
y = 1,5х – 1
|
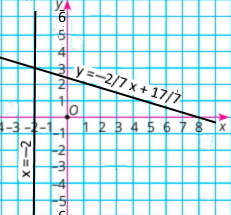
х = –2 |
y = –2/7 х + 17/7
|
||||||||||||
|
Розв'язок (2;2) |
Розв'язок (-2;3) |
||||||||||||||
Завдання 1297
|
{2х + у = 5 |•3 6х + ау = 15 {6x + 3y = 15 6x + ay = 15 Система рівнянь має безліч розв'язків при а = 3 |
2) {Зх – 2у = 7 |•(–2) –6x + 4y = a {–6x + 4y = –14 –6x + 4y = a Система рівнянь не має розв'язків при a ≠ –14 |
До § 28
Завдання 1298 Розв'язування системи рівнянь способом підстановки
|
1) {х = у – 7 2x – y = –6 {x = y – 7 2(y – 7) – y = –6 Розв'язуємо рівняння: 2(y – 7) – y = –6 2y – 14 – y = –6 y = 8 Підставляємо у в рівняння х = у – 7: x = 8 – 1 = 7 Відповідь: (7;8) |
2) {2х + у = 1 3x – 5y = 21 {y = 1 – 2x 3x – 5(1 – 2x) = 21 Розв'язуємо рівняння: 3x – 5(1 – 2x) = 21 3x – 5 + 10x = 21 13x = 26 х = 2 Підставляємо х у рівняння у = 1 – 2х: y = 1 – 2 • 2 = 1 – 4 = –3 Відповідь:(2;–3) |
|
3) {3х – 4у = –19 x + 7y = 27 {3(27 – 7y) – 4y = –19 x = 27 – 7y Розв'язуємо рівняння: 3(27 – 7y) – 4y = –19 81 – 21y – 4y = –19 –25y = –100 y = 4 Підставляємо у в рівняння х = 27 – 7у: х = 27 – 7 • 4 = 27 – 28 = –1 Відповідь: (–1;4) |
4) {5х + 7у = –З 8х – у = –17 {5x + 7(8x + 17) = –3 y = 8x + 17 Розв'язуємо рівняння: 5x + 7(8x + 17) = –3 5x + 56x + 119 = –3 61x = –122 х = –2 Підставляємо х у рівняння у = 8х + 17: y = 8 • (–2) + 17 = –16 + 17 = 1 Відповідь: (–2;1) |
Завдання 1299
Не виконуючи побудови, знайдіть координати точки перетину графіків рівнянь:
|
1) {2x + 3y = 0 4x – 5y = –22 {x = –1,5y 4 • (–1,5y) – 5y = –22 Розв'язуємо рівняння: 4 • (–1,5y) – 5y = –22 –6у – 5у = –22 –11y = –22 у = 2 x = –1,5y, y = 2; Підставляємо у в рівняння х = –1,5у: x = –1,5 • 2 = –3 Координати точки (–3;2) |
2) {4x – 7y = 34 2x + 7y = –4 {7y = 4х – 34 2x + (4х – 34) = –4 Розв'язуємо рівняння: 2x + (4х – 34) = –4 2x + 4х – 34 = –4 6х = 30 x = 5 Підставляємо х у рівняння 7у = 4х – 34: 7у = 4 • 5 – 34 7y = –14 y = –2 Координати точки (5;–2) |
Завдання 1300
|
1) {3(y – x) – 4 = –7у 5(x + у) + 9 = 8x {3y – 3x – 4 = –7y 5x + 5y + 9 = 8x {10y – 3x = 4 5y – 3x = –9 {3x = 10y – 4 5y – (10у – 4) = –9 Розв'язуємо рівняння: 5y – (10y – 4) = –9 5y – 10y + 4 = –9 –5y = –13 y = 13/5 = 2 3/5 Підставляємо у в рівняння 3х = 10у – 4: 3х = 10 • 13/5 – 4 3х = 26 – 4 3у = 22 у = 22/3 = 7 1/3 Відповідь: (7 1/3;2 3/5) |
2) {x/2 + y = 5 |•2 x – y/3 = 3 |•3 {x + 2y = 10 3x – y = 9 {x = 10 – 2y 3(10 – 2y) – y = 9 Розв'язуємо рівняння: 3(10 – 2y) – y = 9 30 – 6y – y = 9 –7y = –21 y = 3 Підставляємо у в рівняння х = 10 – 2у: x = 10 – 2 • 3 = 10 – 6 = 4 Відповідь: (4;3)
|
Завдання 1301
Розв'яжіть систему рівнянь:
{(2x – 1)/3 + (y + 7)/2 = 5,
(3x – 1)/5 + (2y + 1)/3 = (6x + 8y)/15
{(2x – 1)/3 + (y + 7)/2 = 5 |•6
(3x – 1)/5 + (2y + 1)/3 = (6x + 8y)/15 |•15
{2(2x – 1) + 3(y + 7) = 30
3(3x – 1) + 5(2y + 1) = 6x + 8y
{4x – 2 + 3y + 21 = 30
9x – 3 + 10y + 5 = 6x + 8y
{4x + 3y = 11
3x + 2y = –2
{y = (–2 – 3x)/2
4x + 3((–2 – 3x)/2) = 11
Розв'язуємо рівняння:
4x + 3((–2 – 3x)/2) = 11 |•2
8x + 3(–2 – 3x) = 22
8x – 6 – 9x = 22
x = –28
Підставляємо знайдене значення змінної х у рівняння у = (–2 – 3х)/2:
y = (–2 – 3 • (–28))/2 = (–2 + 84)/2 = 82/2 = 41
Відповідь: (–26;41)
Завдання 1302
Розв'яжіть рівняння з двома змінними:
|
1) |x – y| + (x + 2y – 1)² = 0 Сума невід'мних доданків дорівнює 0, коли кожен з доданків дорівнює 0. {|x – y| = 0 (x + 2y – 1)² = 0 {x – y = 0 x + 2y – 1 = 0 {x = y y + 2y – 1 = 0 Розв'язуємо рівняння: y + 2y – 1 = 0 3у = 1 у = 1/3 Підставляємо у в рівняння х = у: x = 1/3 Відповідь: (1/3;1/3) |
2) |x + y – 6| + x² – 4xy + 4y² = 0 |x + y – 6| + (x – 2y)² = 0 Сума невід'мних доданків дорівнює 0, коли кожен з доданків дорівнює 0. {|x + y – 6| = 0 (x – 2y)² = 0 {x + y – 6 =0 x – 2y = 0 {2у + y – 6 = 0 x = 2y Розв'язуємо рівняння: 2у + y – 6 =0 3y = 6 у = 2 Підставляємо у в рівняння х = 2у: х = 2 • 2 = 4 Відповідь: (4;2) |
До § 29
Завдання 1303 Розв'язування системи рівнянь способом додавання
|
1) {2х + у = З 3x – y = 7 5x = 10 x = 2 Підставляємо х у рівняння 2х + у = 3: 2 • 2 + у = 3 4 + у = 3 у = 3 – 4 у = –1 Відповідь: (2;–1)
|
2) {5х + у = 6 |•(–1) 5x + 9y = 14 {–5x – y = –6 5x + 9y = 14 8y = 8 y = 1 Підставляємо у в рівняння 5х + у = 6: 5х + 1 = 6 5х = 5 х = 1 Відповідь: (1;1) |
3) {x + 9y =–7 |•(–3) 3x – 7y = 13 {–3x – 27y = 21 3x – 7y = 13 –34y = 34 y = –1 Підставляємо у в рівняння х + 9у = –7: x + 9 • (–1) = –7 х – 9 = –7 х = 2 Відповідь: (–7;2) |
4) {4x – 5y =2 |•3 7x + 15y = 51 {12x – 15y = 6 7x + 15y = 51 19x = 57 x = 3 Підставляємо х у рівняння 4х – 5у = 2: 4 • 3 – 5у = 2 12 – 5у = 2 –5у = –10 у = 2 Відповідь: (3;2) |
Завдання 1304
|
1) {7х + 2у = 3 |•(–3) 4х + 3у = –2 |•2 {–21x – 6y = –9 8x + 6y = –4 –13x = –13 x = 1 Підставляємо х у рівняння 7 + 2у = 3: 7 • 1 + 2у = 3 2y = –4 y = –2 Відповідь: (1;–2)
|
2) {7х +12у = 53 |•3 5x – 18у = –2 |•2 {21x + 36y = 159 10x – 36y = –4 31x = 155 x = 5 Підставляємо х у рівняння 7х + 12у = 53: 7 • 5 + 12у = 53 35 + 12y = 53 12y = 18 y = 1,5 Відповідь: (5;1,5) |
|
3) 4x + 7y = –5 |•(–3) 6x + 9y = –6 |•2 –12x – 21y = 15 12x + 18y = –12 –3y = 3 y = –1 Підставляємо у в рівняння 4х + 7у = –5: 4x + (–7) = –5 4х – 7 = –5 4x = 2 x = 0,5 Відповідь: (0,5;–1) |
4) {5(a – 3b) + 6a = 7 0,5(a + 6b) – 1,5b = 2,5 {5a – 15b + 6a = 7 0,5a + 3b – 1,5b = 2,5 {11a – 15b = 7 0,5a + 1,5b = 2,5 |•10 {11a – 15b = 7 5a + 15b = 25 16a = 32 a = 2 Підставляємо у в рівняння 11а – 15b = 7: 11 • 2 – 15b = 7 22 – 15b = 7 15b = 15 b = 1 Відповідь: (2;1) |
Завдання 1305
З'ясуйте кількість розв'язків системи рівнянь залежно від коефіцієнта a.
{2x + y = 3 |•2
4x + ay = 6
{4x + 2y = 6
4x + ay = 6
Якщо a = 2, то система має безліч розв’язків.
Якщо a ≠ 2, то система має один розв’язок.