ГДЗ Істер геометрія 7 клас кут, вимірювання кутів, бісектриса кута (відповіді)

Інші завдання дивись тут...

Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."

^{(умови завдань з підручника подані чорним кольором)}

§3 Кут, вимірювання кутів, бісектриса кута

Завдання 39 Малюнок 3.9

Для кута АМК вершина А, сторони МА, МК.

Для кута PLF вершина L, сторони LP, LF.

Для кута BNC вершина N, сторони NB, NC.

Завдання 40

Для кута MOP вершина О, сторони ОМ, ОР.

Для кута BLK вершина L, сторони LB, LK.

Завдання 41

1) ∠A = 39° гострий кут;

2) ∠B = 90° прямий кут;

3) ∠C = 91° тупий кут;

4) ∠D = 170° тупий кут;

5) ∠M = 180° розгорнутий кут;

6) ∠Q = 79° гострий кут;

7) ∠P = 1° 3' гострий кут;

8) ∠F = 173° 12' тупий кут;

9) ∠K = 89° 30' гострий кут.

Завдання 42

1) ∠K = 121° тупий кут;

2) ∠A = 90° прямий кут;

3) ∠L = 12° гострий кут;

4) ∠E = 180° розгорнутий кут;

5) ∠M = 89° гострий кут;

6) ∠N = 93°12' тупий кут.

Завдання 43

1) На малюнку 3.10 промінь OK не є бісектрисою кута AOB, оскільки не ділить кут навпіл.

∠АОК = 50°, ∠КОВ = 30°, ∠АОК ≠ ∠ КОВ.

2) На малюнку 3.11 промінь OK є бісектрисою кута AOB, оскільки ділить кут навпіл.

∠АОК = 60°, ∠КОВ = 60°, ∠АОК = ∠КОВ.

3) На малюнку 3.12 промінь OK є бісектрисою кута AOB, оскільки ділить кут навпіл.

∠АОК = 120°, ∠КОВ = 120°, ∠АОК = ∠КОВ.

Завдання 44 Малюнок 3.13

1) Усі зображені кути: кут АВС, або кут СВА; кут ABD, або кут DBA; кут DBC, або кут CBD.

2) Градусні міри кутів АBD і DBC:

∠АВD = 65°

∠DBC = 65°

3) градусна міра третього кута:

∠АВС = 130°

Завдання 45

Знайдіть градусні міри кутів на малюнку 3.9, визначте вид кожного з них.

∠AMK = 40° гострий кут

∠PLF = 90° прямий кут

∠BNC = 105° тупий кут

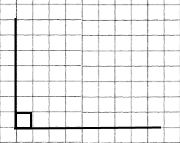
Завдання 46

1) 30°	2) 90°

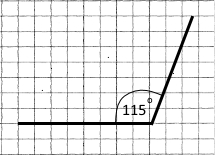
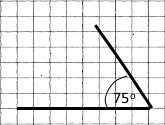
3) 115°	4) 75°

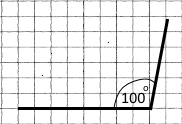
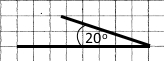
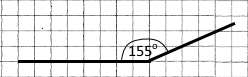
Завдання 47

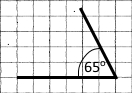
1) 65°	2) 100°
_
3) 20°	4) 155°

Завдання 48

Накресліть кут, градусна міра якого дорівнює 140°, і проведіть його бісектрису.

Бісектриса ділить кут на два рівні кути.

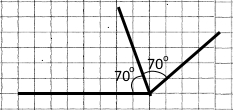
Завдання 49

Накресліть кут, градусна міра якого дорівнює 50°, і проведіть його бісектрису.

Завдання 50

1) 7°13' + 12°49' = (7° + 12°) + (13' + 49') = 19° + 62' = 19° + 1° + 2' = 20°2'

2) 52°17' – 45°27' = 51°77' – 45°27' = (51° – 45°) + (77' – 27') = 6° + 50' = 6°50'

Завдання 51

1) 4° = 4° • 60 = 240'

2°15' = 2° • 60 + 15' = 120' + 15' = 135'

2) 5' = 5' • 60 = 300”

2° = 2° • 3600 = 7200”

1°3' = 1° • 3600 + 3' • 60 = 3600” + 180” = 3780”

Завдання 52

Промінь OK проходить між сторонами кута BOC. Знайдіть градусну міру кута BOC, якщо ∠BOK = 38°, ∠KOC = 42°. Виконайте малюнок.

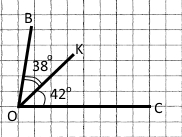
Якщо промінь ОК проходить між сторонами кута ВОС, тоді справедлива основна властивість вимірювання кутів ∠ВОС = ∠ВОК + ∠КОС.

∠ВОС = ∠ВОК + ∠КОС = 38° + 42° = 80°

Завдання 53

Промінь PC проходить між сторонами кута APB. Знайдіть градусну міру кута CPB, якщо ∠APB = 108°, ∠APC = 68°. Виконайте малюнок.

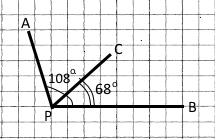
Якщо промінь РС проходить між сторонами кута АРВ, тоді справедлива основна властивість вимірювання кутів: ∠АРВ = ∠АРС + ∠СРВ.

∠СРВ = ∠АРВ – ∠АРС = 108° – 68° = 40°

Завдання 54

Чи проходить промінь BK між сторонами кута ABC, якщо ∠ABC = 52°, ∠ABK = 57°? Відповідь обґрунтуйте.

Якщо промінь ВК проходить між сторонами кута АВС, тоді справедлива основна властивість вимірювання кутів ∠АВС = ∠АВК + ∠КАС.

52° < 57° + ∠КАС

Оскільки не виконується основна властивість, отже, промінь ВК не проходить між сторонами кута АВС.

Завдання 55

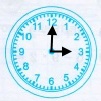
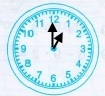
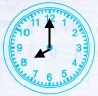
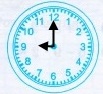
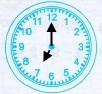
Знайдіть градусні міри кутів між годинною та хвилинною стрілками годинника.

Годинник має 12 поділок, у середині кола годинника градусна міра дорівнює 360, тоді 360 : 12 = 30 (°) – градусна міра між сусідніми поділками.

Кожної години хвилинна стрілка знаходиться біля поділки 12, а годинна стрілка вказує час. Щоб знайти градусну міру між годинною та хвилинною стрілками годинника достатньо градусну міру між сусідніми стрілками помножити на число, біля якого знаходиться годинна стрілка.

1) о 18 год	2) о 3 год	3) о 1 год	4) о 20 год
30° • 6 = 180°	30° • 3 = 90°	30° • 1 = 30°	30° • 8 = 240°

Завдання 56

Знайдіть градусну міру кута між годинною та хвилинною стрілками годинника.

1) о 21 год	2) о 6 год	3) о 19 год	4) о 2 год
30° • 9 = 270°	30° • 6 = 180°	30° • 7 = 210°	30° • 2 = 60°

Завдання 57

Промінь OC ділить кут AOB на два кути. Знайдіть градусну міру кута BOC, якщо ∠AOB = 60° і ∠AOC = 2/3 ∠AOB.

Якщо промінь ОС проходить між сторонами кута АОС, тоді справедлива основна властивість вимірювання кутів ∠АОВ = ∠АОС + ∠СОВ.

∠ВОС = ∠СОВ = ∠АОВ – ∠АОС = ∠АОВ – 2/3 ∠АОВ = (3/3 – 2/3) • ∠АОВ = 1/3 ∠АОВ = 1/3 • 60° = 60°/3 = 20°

2 спосіб

∠АОС = 2/3 ∠АОВ = ∠АОВ • 2 : 3 = 60° • 2 : 3 = 40°

∠ВОС = ∠СОВ = ∠АОВ – ∠АОС = 60° – 40° = 20°

Відповідь: ∠ВОС = 20°

Завдання 58

Промінь AB ділить кут MAK на два кути. Знайдіть градусну міру кута MAK, якщо ∠MAB = 70°, а кут BAK становить 60% від кута MAB (∠ВАК = 0,60 ∠МАВ).

Якщо промінь АВ ділить кут МАК на два кути, тоді справедлива основна властивість вимірювання кутів ∠МАК = ∠МАВ + ∠ВАК.

∠МАК = ∠МАВ + 0,6 ∠МАВ = (1,0 + 0,6) • ∠МАВ = 1,6 ∠МАВ = 1,6 • 70° = 112°

2 спосіб

∠ВАК = 0,6 ∠МАВ = 0,6 • ∠МАВ = 0,6 • 70° = 42°

∠МАК = ∠МАВ + ∠ВАК = 70° + 42° = 112°

Відповідь: ∠МАК = 112°

Завдання 59

Кут між бісектрисою кута і продовженням однієї з його сторін за вершину кута дорівнює 142°. Знайдіть градусну міру цього кута.

Бісектриса ділить кут пополам, тоді градусна міра такого кута дорівнює подвійній величині одного з утворених кутів.

142° • 2 = 284°

Завдання 60

Який кут утворює бісектриса кута 98° з продовженням однієї з його сторін за вершину кута?

98° • 2 = 196°

Завдання 61

1) ∠MQB = 120°. Між сторонами кута проходить промінь QP. Знайдіть кути PQB і MQP, якщо кут PQB у 4 рази менший від кута MQP.

Якщо промінь QP проходить між сторонами кута MQB, тоді справедлива основна властивість вимірювання кутів ∠МQB = ∠MQP + ∠PQB.

120 : 5 = 24 (°) – градусна міра кута PQB, або припадає на 1 частину кута MQB (У).

24 • 4 = 96 (°) – градусна міра кута MQP (К)

2) ∠MQB = 120°. Між сторонами кута проходить промінь QP. Знайдіть кути PQB і MQP, якщо ∠PQB : ∠MQP = 3 : 2.

120 : 5 = 24 (°) – припадає на 1 частину кута MQB.

24 • 3 = 72 (°) – градусна міра кута РQВ (Р)

24 • 2 = 48 (°) – градусна міра кута MQP (Ч)

3) ∠MQB = 120°. Між сторонами кута проходить промінь QP. Знайдіть кути PQB і MQP, якщо кут PQB на 20° більший за кут MQP.

120 – 20 = 100 (°) – подвійна градусна міра кута MQР.

100 : 2 = 50 (°) – градусна міра кута МQР (В)

50 + 20 = 70 (°) – градусна міра кута РQВ (А)

96°	72°	70°	50°	48°	24°	96°
К	Р	А	В	Ч	У	К

2) Відомих українців із цим прізвищем знаєте: перший президент незалежної України.

Завдання 62

1) Промінь AC проходить між сторонами кута MAN, який дорівнює 84°. Знайдіть кути MAC і CAN, якщо кут MAC більший за кут CAN на 14°.

Якщо промінь АС проходить між сторонами кута MAN, тоді справедлива основна властивість вимірювання кутів ∠МAN = ∠MAC + ∠CAN.

84 – 14 = 70 (°) – подвійна градусна міра кута CAN.

70 : 2 = 35 (°) – градусна міра кута CAN (А)

35 + 14 = 49 (°) – градусна міра кута MAC (Р)

2) Промінь AC проходить між сторонами кута MAN, який дорівнює 84°. Знайдіть кути MAC і CAN, якщо кут MAC менший від кута CAN у 3 рази.

84 : 4 = 21 (°) – градусна міра кута МАС, або одна частина кут MAN (В).

21 • 3 = 63 (°) – градусна міра кута CAN (Ш)

Назва столиці європейської держави Польщі:

21°	35°	49°	63°	35°	21°	35°
В	А	Р	Ш	А	В	А

2) Дізнайтеся про відстань від Києва до цієї столиці та складіть задачу, пов'язану із зазначеною відстанню.

Відстань між Києвом і Варшавою становить 782 км. Автобус рухається рівномірно зі швидкістю 46 км/год. Скільки часу пасажир буде в дорозі?

^{Швидкість, км/год}	^{Час, год}	^{Відстань, км}
⁴⁶	^?	⁷⁸²

782 : 46 = 17 (год)

Відповідь: 17 годин.

Завдання 63

Розгорнутий AOB променями OK і OL поділено на три кути так, що ∠AOK = 140°, ∠BOL = 100°. Знайдіть градусну міру кута LOK.

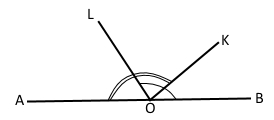
Кут АОВ розгорнутий, тому ∠АОВ = 180.

Якщо промені ОL і OK проходить між сторонами кута AOB, тоді справедлива основна властивість вимірювання кутів ∠AOB = ∠AOL + ∠LOK + ∠KOB

∠LOK = ∠AOB – ∠AOL – ∠KOB

∠AOL = ∠AOB – ∠LOB = ∠AOB – ∠BOL = 180° – 100° = 80°

∠KOB = ∠AOB – ∠AOK = 180° – 140° = 40°

∠LOK = 180° – 80° – 40° = 60°

Відповідь: ∠LOK = 60°

Завдання 64

Прямий кут COD променями OM і ON поділено на три кути так, що ∠CON = 70°, ∠MOD = 80°. Знайдіть градусну міру кута MON.

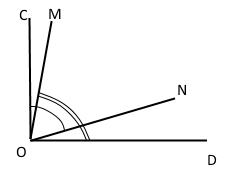
Кут COD прямий, тому ∠COD = 90°

Якщо промені ОM і ON проходить між сторонами кута COD, тоді справедлива основна властивість вимірювання кутів: ∠COD = ∠COM + ∠MON + ∠NOD.

∠MON = ∠COD – ∠COM – ∠NOD

∠COM = ∠COD – ∠MOD = 90° – 80° = 10°

∠NOD = ∠COD – ∠CON = 90° – 70° = 20°

∠MON = 90° – 10° – 20° = 60°

Відповідь: ∠MON = 60°

Завдання 65

1) Фермерська родина Нечипоруків посіяла огірки в теплиці 28 м 50 см завдовжки і 16 м завширшки. Скільки кілограмів огірків збере родина з теплиці, якщо з 1 м² збирають 30 кг огірків?

^{Маса на 1м2 (кг)}	^{Загальна площа (м2)}	^{Загальна маса (кг)}
^{30 кг}	^S	^?

28 м 50 см = 28 • 100 см + 50 см = 2850 см

16 м = 16 • 100 см = 1600 см

1) S = 2850 • 1600 = 4560000 (см2) = 456 • 100 • 100 (см2) = 456 (м2) – площа ділянки.

2) 30 • 456 = 13680 (кг) = 13 т 680 кг – огірків збере.

Відповідь: родина збере 13 т 680 кг огірків.

2) Фермерська родина Нечипоруків збере 13 680 кг огірків. Який виторг отримають фермери, якщо продадуть огірки під час весняного сезонного підвищення цін на овочі за ціною 18 грн за кілограм?