Серія "Вчимось разом" до підручника "Геометрія 7 клас Істер О."
(умови завдань з підручника подані чорним кольором)
§ 11 Трикутник і його елементи
Завдання 281
Три сторони трикутника KLM відповідно дорівнюють ML = 4 см, MK = 2 см, KL = 3 см. Знайдіть периметр трикутника KLM.
Короткий запис
І сторона — 4 см
ІІ сторона — 2 см
ІІІ сторона — 3 см
Р — ?
Розв’язання
Р = 4 + 2 + 3 = 9 (см)
Завдання 282
Накресліть ∆PKL. Запишіть вершини, сторони та кути цього трикутника.
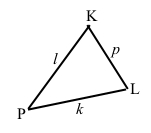
Вершини: P, K, L.
Сторони: PK (або KP), KL (або LK), PL (або LP).
Сторони можемо також позначити p, k, l.
Кути: ∠PKL (або ∠LKP), ∠KLP (або ∠PLK), ∠LPK (або ∠KPL).
Оскільки з вершин не проведено жодних інших ліній, тоді кути можемо позначити ∠P, ∠K, ∠L.
Завдання 283
Накресліть трикутник і позначте його вершини буквами A, М і N. Назвіть сторони і кути цього трикутника.
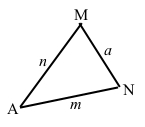
Сторони: AM (або MA), MN (або NM), NA (або AN).
Сторони можемо також позначити a, m, n.
Кути: ∠AMN (або ∠NMA), ∠MNA (або ∠ANM), ∠NAM (або ∠MAN).
Оскільки з вершин не проведено жодних інших ліній, тоді кути можемо позначити ∠A, ∠M, ∠N.
Завдання 284
На малюнку 11.2 і 11.4 три точки можуть бути вершинами трикутника, оскільки не лежать на одній прямій.
На малюнку 11.3 три точки не можуть бути вершинами трикутника, оскільки вони лежать на одній прямій.
Завдання 285
Знайдіть периметр трикутника зі сторонами 25 мм, 3,2 см (32 мм), 0,4 дм (40 мм).
Короткий запис
І сторона — 25 мм
ІІ сторона — 32 мм
ІІІ сторона — 40 мм
Р — ?
Розв’язання
3,2 см = 1 см • 3,2 = 10 мм • 3,2 = 32 мм
0,4 дм = 1 дм • 0,4 = 100 мм • 0,4 = 40 мм
Р = 25 + 32 + 40 = 97 (мм) = 9 см 7 мм
Відповідь: периметр трикутника 9 см 7 мм.
Завдання 286
Знайдіть периметр трикутника, сторони якого дорівнюють 4,3 см, 29 мм, 0,3 дм.
Короткий запис
І сторона — 25 мм
ІІ сторона — 32 мм
ІІІ сторона — 40 мм
Р — ?
Розв’язання
3,2 см = 1 см • 3,2 = 10 мм • 3,2 = 32 мм
0,4 дм = 1 дм • 0,4 = 100 мм • 0,4 = 40 мм
Р = 25 + 32 + 40 = 97 (мм) = 9 см 7 мм
Відповідь: периметр трикутника 9 см 7 мм.
Завдання 287
Накресліть гострокутний ∆ABC. Виміряйте його сторони та знайдіть його периметр.
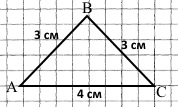
Короткий запис
І сторона — 3 см
ІІ сторона — 3 см
ІІІ сторона — 4 см
Р — ?
Розв’язання
Р = 3 + 3 + 4 = 10 (см)
Відповідь: Р = 10 см.
Завдання 288
Накресліть тупокутний трикутник, вершинами якого є точки P, L і K. Виміряйте сторони цього трикутника та знайдіть його периметр.
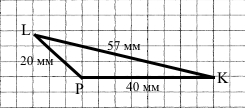
Короткий запис
І сторона — 20 мм
ІІ сторона — 57 мм
ІІІ сторона — 40 мм
Р — ?
Розв’язання
Р = 20 + 57 + 40 = 117 (мм) = 11 см 7 мм
Відповідь: Р = 11 см 7 мм.
Завдання 289
Одна сторона трикутника втричі менша від другої і на 7 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 32 см.
Периметр трикутника – сума довжин трьох його сторін.
Нехай х (см) – перша сторона, тоді 3х (см) – друга сторона, х + 7 (см) – третя сторона. Складемо рівняння.
х + 3х + (х + 7) = 32
5х + 7 = 32
5х = 32 – 7
5х = 25
х = 25 : 5
х = 5 (см) – І сторона.
3х = 2 • 3 = 15 (см) – ІІ сторона.
х + 7 = 5 + 7 = 12 (см) – ІІІ сторона.
Відповідь: І сторона – 5 см, ІІ сторона – 15 см, ІІІ сторона – 12 см.
Завдання 290
Одна сторона трикутника на 2 дм більша за другу і в 1,5 рази менша від третьої сторони. Знайдіть сторони трикутника, якщо його периметр дорівнює 40 дм.
Периметр трикутника – сума довжин трьох його сторін.
Нехай х (дм) – одна сторона, тоді х – 2 (дм) – друга сторона, 1,5х (дм) – третя сторона. Складемо рівняння.
х + (х – 2) + 1,5х = 40
3,5х – 2 = 40
3,5х = 40 + 2
3,5х = 42
х = 42 : 3,5
х = 12 (дм) – І сторона.
х – 2 = 12 – 2 = 10 (дм) – ІІ сторона.
1,5х = 12 • 1,5 = 18 (см) – ІІІ сторона.
Відповідь: І сторона – 12 дм, ІІ сторона – 10 дм, ІІІ сторона – 18 дм.
Завдання 291
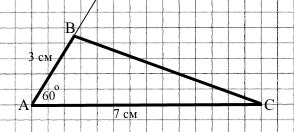
Використовуючи лінійку з поділками та транспортир, побудуйте ∆ABC, у якого ∠A = 60°, AB = 3 см, AC = 7 см.
1) За допомогою лінійки відкладемо сторону АС = 7 см.
2) Від точки А за допомогою транспортира відкладемо кут ∠A = 60°.
3) На цій стороні кута за допомогою лінійки відкладемо відрізок АВ = 3 см.
4) За допомогою лінійки сполучимо відрізком точки В і С.
Завдання 292
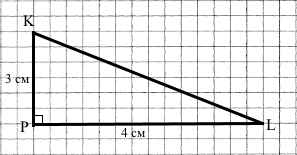
Побудуйте за допомогою лінійки з поділками та косинця ∆PKL, у якого ∠P = 90°, PK = 3 см, PL = 4 см. Як називають такий трикутник? Виміряйте довжину сторони KL.
1) За допомогою лінійки відкладемо сторону PL = 4 см.
2) Від точки Р за допомогою косинця відкладемо прямий кут ∠Р = 90° та відрізок РК = 3 см.
4) Сполучимо відрізком точки K і L.
5) Утворився прямокутний трикутник.
6) За допомогою лінійки виміряли довжину третьої сторони KL = 5 см.
Завдання 293
Знайдіть сторони трикутника, якщо вони пропорційні числам 3, 4 і 6 (відносяться як 3 : 4 : 6), а периметр трикутника дорівнює 52 дм.
Периметр трикутника – сума довжин трьох його сторін.
Нехай 3х (дм) – перша сторона, тоді 4х (дм) – друга сторона, 6х (дм) – третя сторона. Складемо рівняння.
3х + 4х + 6х = 52
13х = 52
х = 52 : 13
х = 4 (дм) – довжина 1 частини.
3х = 4 • 3 = 12 (дм) – І сторона (3 частини).
4х = 4 • 4 = 16 (дм) – ІІ сторона (4 частини).
6х = 4 • 6 = 24 (дм) – ІІІ сторона (6 частин).
Відповідь: І сторона – 12 дм, ІІ сторона – 16 дм, ІІІ сторона – 24 дм.
Завдання 294
Периметр трикутника дорівнює 72 см. Знайдіть сторони цього трикутника, якщо вони пропорційні числам 2, 3 і 4 (відносяться як 2 : 3 : 4).
Периметр трикутника – сума довжин трьох його сторін.
Нехай 2х (см) – перша сторона, тоді 3х (см) – друга сторона, 4х (см) – третя сторона. Складемо рівняння.
2х + 3х + 4х = 72
9х = 72
х = 72 : 9
х = 8 (см) – довжина 1 частини.
2х = 8 • 2 = 16 (см) – І сторона (2 частини).
3х = 8 • 3 = 24 (см) – ІІ сторона (3 частини).
4х = 8 • 4 = 32 (см) – ІІІ сторона (4 частини).
Відповідь: І сторона – 16 см, ІІ сторона – 24 см, ІІІ сторона – 32 см.
Завдання 295
Укажіть, скількома способами можна назвати трикутник з вершинами в точках M, N і K.
Можна назвати 6 способами:
∆MNK, ∆MКN,
∆NKM, ∆NMК,
∆KMN, ∆KNМ.
Завдання 296
Сума першої і другої сторін трикутника дорівнює 11 см, другої і третьої – 14 см, а першої і третьої – 13 см. Знайдіть периметр трикутника.
Короткий запис
І і ІІ — 11 см
ІІ і ІІІ — 14 см
ІІІ і І — 13 см
Р — ?
Розв’язання
1) 11 + 14 + 13 = 38 (см) – подвійний периметр трикутника (подвійна довжина всіх його сторін).
2) 38 : 2 = (20 + 18) : 2 = 19 (см) – периметр трикутника.
Відповідь: Р = 19 см.
Вправи для повторення
Завдання 297
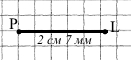
Накресліть відрізок AB завдовжки 2 см 7 мм. Накресліть відрізок PL, що дорівнює відрізку AB.
Відрізки рівні, якщо рівні їх довжини.
PL = 2 см 7 мм
PL = AB
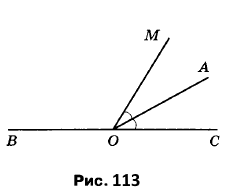
Завдання 298 Який кут утворює бісектриса кута 78° з променем, що є доповняльним до однієї з його сторін?
За умовою кут ∠СОМ = 78°.
ОС – доповняльний промінь, тому маємо розгорнутий кут ∠ВОС = 180°. За основною властивістю вимірювання кутів ∠ВОС = ∠ВОМ + ∠МОС, тоді ∠ВОМ = ∠ВОС – ∠СОМ = 180° – 78° = 102°.
ОА – бісектриса кута ∠СОМ = 2∠АОМ, ∠АОМ = ∠СОМ : 2 = 78° : 2 = 39°.
За основною властивістю кута ∠ВОА = ∠ВОМ + ∠АОМ = 102° + 39° = 141°.
Доповняльний промінь до однієї зі сторін трикутника утворює розгорнутий кут, а також два суміжні кути. Інший суміжний кут 180° – 78° = 102°.
Бісектриса кута ділить його пополам 78° : 2° = 39°.
Бісектриса даного кута з променем, що є доповняльним до однієї з його сторін, утворює кут 102° + 39° = 141°.
Відповідь: 141°.
Життєва математика
Завдання 299
1) Відомо, що 1 га лісу очищує за рік 18 млн м3 повітря. Скільки м3 повітря очистить за рік ліс площею 3 га?
Короткий запис
1 га — 18 млн м3
3 га — ? млн м3
Розв’язання
1) 18 • 3 = 48 (м3)
Відповідь: ліс очистить 48 м3 повітря.
2) Відомо, що 1 га лісу очищує за рік 18 млн м3 повітря. Скільки м3 повітря очистить за рік ліс площею 2 км2?
1 га = 100 м • 100 м = 10 000 м2
2 км2 = 2 • 1 км • 1 км = 2 • 1000 м • 1000 м = 2 000 000 м2 = (2 000 000 : 10 000) га = 200 га
Короткий запис
1 га — 18 млн м3
200 га — ? млн м3
Розв’язання
1) 18 • 200 = 4800 (м3)
Відповідь: ліс очистить 4800 м3 повітря.
Завдання 300
У п'ятикутній зірці 5 чотирикутників.
