Завдання 1 Функція
Б. y = 4/(x – 3)
Завдання 2 Лінійна функція
A. у = х – 2
Завдання 3 Функція прямої пропорційності
B. у = 2х
Завдання 4
Обчисліть значення функції у = –20/x, для значення аргументу, що дорівнює –4.
Якщо x = –4, тоді y = –20/(–4) = 5, тому Г. 5
Завдання 5
Не виконуючи побудови, знайдіть нуль функції у = 1/3х – 2.
Якщо y = 0, тоді 0 = 1/3x – 2; 1/3x = 2; х = 6, тому B. 6
Завдання 6
Графік функції y = 3 – х зображено на рисунку А)
Завдання 7
Знайдіть область визначення функції у = 3/(x² + x).
Областю визначення функції y = 3/(x²+ x) є всі числа, крім тих, для яких:
x² + х ≠ 0
х(х + 1) ≠ 0
x ≠ 0 i x + 1 ≠ 0
x ≠ 0 i x ≠ –1
Відповідь: Г. Усі числа, крім 0 і –1.
Завдання 8
Графіку функції y = x² – 2х належить точка (1; –1), бо
–1 = 1² – 2 • 1;
–1 = 1 – 2;
–1 = –1.
Відповідь: Б. (1; –1).
Завдання 9
Укажіть точку перетину графіка функції у = 0,1х + 15 з віссю абсцис.
Якщо y = 0, тоді 0 = 0,1х + 15; 0,1х = –15; х = –150, тому B. (–150; 0)
Завдання 10
Знайдіть для х = 2 значення функції
y = {7, якщо х < 0,
х², якщо 0 ≤ х < 3,
5х, якщо х ≥ 3.
Значення х = 2 задовольняє умову 0 ≤ х < 3, отже, значення функції обчислюємо за
формулою у = x² : y = 2²; у = 4, тому А. 4
Завдання 11
Графік прямої пропорційності проходить через точку Р(2; –4). Укажіть точку, через яку також проходить цей графік.
у = kх; –4 = k • 2; k = –2, рівняння має вигляд у = –2х.
Дане рівняння задовольняє лише точка (3; –6), тому Б. (3; 6)
Завдання 12
Не будуючи графіка функції у = 3х – 8, знайдіть таку його точку, абсциса й ордината якої є протилежними числами.
Якщо y = –х, тоді –x = 3x – 8; 4х = 8; x = 2 і у = –2, тому Б. (2; –2)
Завдання 13
Установіть відповідність між функціями (1–3) та точками, у яких графік функції перетинає осі координат (А–Г).
| Функції | Точки |
|
1. y = 4 – 2x 2. y = 4 3. y = x – 4 |
А. (0; 4) Б. (0; 4), (4; 0) В. (0; 4), (2; 0) Г. (0; –4), (4; 0) |
Відповідь: 1 – В. (0; 4), (2; 0); 2 – А. (0; 4); 3 – Г. (0; –4), (4; 0).
ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ ДО §§ 22–24
Завдання 1 Функції
1) y = x² + x
2)у = (x – 1)/(у + 2)
3) y = 1/(x – 8)
4) xy = (x – y)²
Завдання 2 Лінійні функції
1) y = 3x – 7
2) y = x² – 5
3) y = 4
4) у = 1/(2x – 4)
Завдання 3
1) для лінійної функції y = –2x + 6 значення коефіцієнтів k = –2, l = 6
2) для лінійної функції y = 7,4x значення коефіцієнтів k = 7,4, l = 0
Завдання 4
Функцію задано формулою y = –2x + 7. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 5;
Якщо х = 5, тоді у = –2 • 5 + 7; у = –10 + 7; у = –3
2) значення аргументу, якщо значення функції дорівнює 3.
у = 5, якщо 3 = –2х + 7; 2х = 7 – 3; 2х = 4; х = 2.
Завдання 5
Побудуйте графік функції y = 2x – 5.
|
х |
0 |
5 |
|
у |
–5 |
5 |
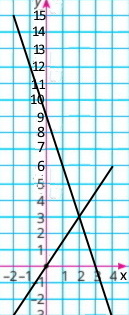
1) значення функції для х = 4; у = 3
2) значення аргументу, для якого у = –3. х = 1
Завдання 6
Функцію задано формулою y = 0,8x – 7,2. Не виконуючи побудови:
1) знайдіть нулі функції;
0 = 0,8х – 7,2; 0,8x = 7,2; х = 9;
2) з'ясуйте, чи проходить графік функції через точку (10; 1).
1 = 0,8 • 10 – 7,2
1 = 8 – 7,2
1 = 0,8 Хибна рівність. Отже, графік функції = 0,8х – 7,2 не проходить через точку (10;1).
Завдання 7
Знайдіть область визначення функції y = 7/(x² – 5x).
х² – 5x = 0
х(х – 5) = 0
х = 0 і х – 5 = 0
х = 0 і х = 5
Отже, областю визначення функції у = 7/(x²– 5x) – є всі числа, крім х = 0 і х = 5.
Завдання 8
Побудуйте в одній системі координат графіки функцій y = –2,5x і y = –5 та знайдіть координати точки їх перетину.
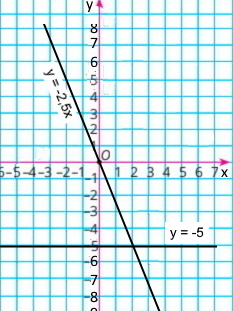
Графіки функцій перетинаються в точці з координатами (2;–5).
Завдання 9
Знайдіть найменше значення функції y = x² – 6x + 11.
x² – 6х + 11 = x² – 6х + 9 + 2 = (х – З)² + 2
у = (х – З)² + 2
(х – З)² ≥ 0, тоді (х – 3)² + 2 ≥ 2. Отже, найменше значення функції дорівнює 2.
Завдання 10
Функцію y = 3x – 7 задано для –2 ≤ x ≤ 5. Знайдіть область значень цієї функції.
Якщо –2 ≤ х ≤ 5, то –6 ≤ 3х ≤ 15; –13 ≤ 3х – 7 ≤ 8; –13 ≤ у ≤ 8.
Завдання 11
Побудуйте графік функції:
у = {2x + 6, якщо х < 0,
6 – х, якщо х ≥ 0.
|
у = 2х + 6 |
у = 6 – х | |||||
|
х |
–2 |
–1 |
|
х |
0 |
1 |
|
у |
2 |
4 |
|
у |
6 |
5 |
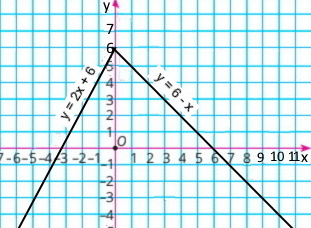
1) нулі функції: x = –3; x = 6
2) значення аргументу, за яких функція набуває додатних значень;
y > 0, якщо –3 < x < 6
3) значення аргументу, за яких функція набуває від'ємних значень.
y < 0, якщо x < –3 або x > 6