До § 22
Завдання 1089
Чи залежить площа квадрата від довжини його сторони? Чи є площа квадрата функцією від довжини сторони квадрата? Якщо так, то задайте цю функцію формулою за умови, що сторона квадрата дорівнює а.
Площа квадрата залежить від довжини його сторони. Ця залежність є функцією, яку можна задати формулою S = а², де а — сторона квадрата.
Завдання 1090
а) Функції задано формулами у = (x + 2)/(x – 3) і g = (x – 4)/5. Заповніть у зошиті таблицю, обчисливши відповідні значення функцій.
у = (x + 2)/(x – 3);
Якщо х = –4 , тоді у = (–4 + 2)/(–4 – 3) = 2/7
Якщо х = –2, тоді y = (–2 + 2)/(–2 – 3) = 0
Якщо х = 0, тоді у = (0 + 2)/(0 – 3) = –2/3
Якщо х = 2, тоді у = (2 + 2)/(2 – 3) = –4
Якщо х = 4, тоді у = (4 + 2)/(4 – 3) = 6
g = (x – 4)/5;
Якщо х = –4, тоді g = (–4 – 4)/5 = –1,6
Якщо х = –2, тоді g = (–2 – 4)/5 = –1,2
Якщо х = 0, тоді g = (0 – 4)/5 = –0,8
Якщо х = 2, тоді g = (2 – 4)/5 = –0,4
Якщо х = 4, тоді g = (4 – 4)/5 = 0
|
x |
–4 |
–2 |
0 |
2 |
4 |
|
y |
2/7 |
0 |
–2/3 |
–4 |
6 |
|
g |
–1,6 |
–1,2 |
–0,8 |
–0,4 |
0 |
Завдання 1091
Із села до міста, відстань між якими дорівнює 48 км, вирушив велосипедист зі швидкістю 14 км/год. Задайте формулою залежність змінної s від змінної t, де s – відстань, яку залишилося подолати велосипедисту до міста (у км), а t – час його руху (у год).
Формула: s = 48 – 14t
1) якщо t = 1,5, тоді s = 48 – 14 ∙ 1,5 = 48 – 21 = 27
2) якщо s = 13, тоді 13 = 48 – 14t; 14t = 48 – 13; 14t = 35; t = 2,5
Завдання 1092 Область визначення функції:
|
1) y = 12/(9x² – 17x); 9х² – 17х = 0 х(9х – 17) = 0 х = 0 або 9х – 17 = 0 х = 0 х = 17/9 = 1 8/9 Область визначення: всі числа, крім 0 і 1 8/9 |
2) у = x/(|x| – 1); │x│ – 1 = 0 │x│ = 1 x = 1 або x = – 1. Область визначення: всі числа, крім –1 і 1 |
3) y = 2/(|x| + 5); Завжди |x| + 5 ≠ 0, Область визначення: всі числа |
|
4) y = 9/(3 – |x – 1|); 3 – |x –1| = 0 |х – 1| = 3 х – 1 = 3 або х – 1 =–3 х = 4 х = –2 Область визначення: всі числа, крім –2 і 4 |
5) y = 15/(|2x – 3| – 5); |2х – З| = 5 2х – 3 = 5 або 2х – 3 =–5 2х = 8 або 2х = –2 x = 4 х = –1 Область визначення: всі числа, крім –1 і 4 |
6) y = 2/(1 – 1/x). 1 – 1/x = 0 1/x = 1 x = 1 Область визначення: всі числа, крім чисел 0 і 1 |
До § 23
Завдання 1093
Функцію задано формулою у = 2x – 3, де – 2 ≤ x ≤ 3.
Заповніть у зошиті таблицю значень функції і побудуйте її графік.
|
x |
–2 |
–1,5 |
–1 |
–0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
y |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
Завдання 1094
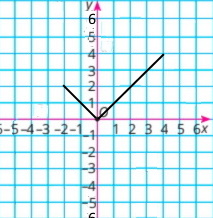
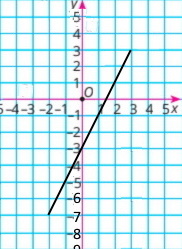
На малюнку 1 зображено графік функції. За графіком знайдіть:
1) Якщо x = –3, то y = –1,5; якщо х = –1,5, то у = –0,5; якщо х = 0, то у = 1;
якщо х = 1,5, то у = 3,5; якщо х = 3, то у = 2;
2) y = –1,5, якщо х = –2 або х = –3, або х = 4; у = 2, якщо х = 0,5 або х = 3;
у = З, якщо х = 1 або х = 2,5;
3) областю визначення функції є всі значення х, такі, що –4 ≤ х ≤ 4;
4) областю значень функції є всі значення у, такі, що –2 ≤ у ≤ 4;
5) Нулі функції: х = –0,5 і х = 3,5
6) функція набуває додатних значень, якщо –0,5 < х < 3,5;
7) функція набуває від’ємних значень, якщо –4 ≤ х < –0,5 і 3,5 < х ≤ 4.
Завдання 1095
Побудуйте графік функції:
|
1) у = |х|, де –2 ≤ х ≤ 4 |
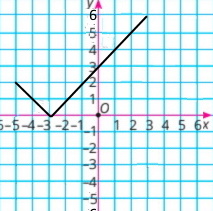
2) у = |х + 3|, де –5 ≤ х ≤ 3 |
||||||||||||||||||||||||||||||
|
у = х, 0 ≤ х ≤ 4
|
у = –х, –2 ≤ х < 0
|
у = –х – 3, –5 ≤ х < –3
|
у = х + 3, –3 ≤ х ≤ 3
|
||||||||||||||||||||||||||||
|
|
 |
||||||||||||||||||||||||||||||
До § 24
Завдання 1096
Які з даних функцій є лінійними? Які з них є прямою пропорційністю:
Лінійні: 1) у = –3х; 2) у = –3х + 4; 6) y = –1/3x
Пропорційні: 1) у = –3х; 6) y = –1/3x
Завдання 1097
Побудуйте графік функції:
|
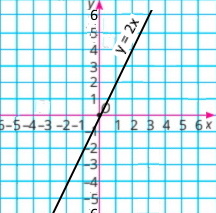
1) у = 2х
|
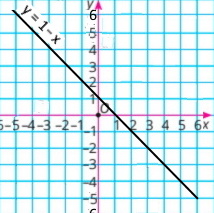
2) у = 1 – х
|
3) у = 2 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
4) у = 4х – 1
|
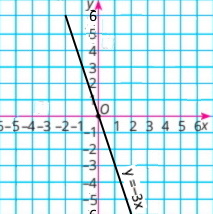
5) у = –3х
|
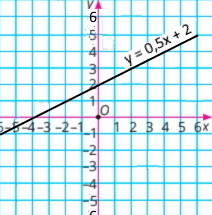
6) у = 0,5х + 2
|
||||||||||||||||||
|
|
|
|
Завдання 1098
Графік прямої пропорційності у = –3/4х.
|
x |
–8 |
–4 |
0 |
4 |
8 |
|
y |
6 |
3 |
0 |
–3 |
–6 |
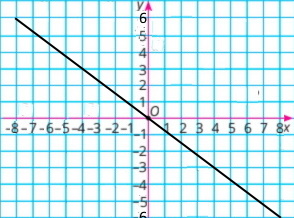
Знайдіть за графіком:
1) якщо x = –4, то y = 3; якщо x = 0, то y = 0; якщо x = 8, то y = –6;
2) якщо x = –6, то y = 8; якщо x = 3, то y = –4; якщо x = 6, то y = –8;
3) якщо x = 0, то y = 0;
4) функція набуває додатних значень, якщо x < 0;
5) функція набуває від'ємних значень, якщо x > 0.
Завдання 1099
Графіки функцій у = kх і у = 2х + l перетинаються в точці А(–2; 6). Знайдіть k і l.
Графік функції у = kх проходить через точку А(–2;4), тому 4 = k • (–2); k = –2
Графік функції у = 2х + l проходить через точку А(–2;4), тому 4 = 2 • (–2) + b; b = 8
Завдання 1100
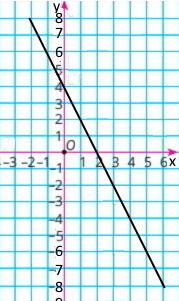
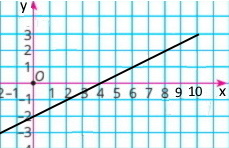
На малюнках 2 і 3 зображено графіки двох процесів. Один з них описує процес наповнення резервуара водою, а другий – процес спорожнення резервуара від води. Який з графіків відповідає кожному зі згаданих процесів? По кожному з графіків знайдіть:
1) На мал. 2 в баку спочатку було 50 л води, а на мал. 3 — 15 л;
2) через 1 хв в баку на мал. 2 було 45 л, а на мал. 3 — 17,5 л;
через 6 хв у баку на мал. 2 було 20 л, а на мал. 3 — 30 л;
через 8 хв в баку на мал. 2 було 10 л, а на мал. 3 — 35 л;
3) у баку на мал. 2 було 25 л води через 5 хв, а у баку на мал. 3 — через 4 хв;
4) щохвилини з баку на мал. 2 виливається 5 л, а в бак на мал. 3 щохвилини надходить 2,5 л;
Формула залежності мал. 2 має вигляд: у = –5х + 50, де 0 ≤ х ≤ 10
Формула залежності мал. 3 має вигляд: у = 2,5х + 15, де 0 ≤ х ≤ 10
Завдання 1101
Побудуйте графік функції.
1) у = 2|x|;
2) y = 5|x| + x;
3 ) y = (|x| – 3x)/2;
4) y = |x| + |–2x|