Завдання 1 Лінійне рівнянням з двома змінними
|
A. 2x² – 3x = 7 |
Б. 2x² – 3y = 7 |
B. 2x – 3y = 7 |
Г. 2x – 3y3 = 7 |
Завдання 2
Укажіть точку, що належить графіку рівняння х + у = 6.
|
A. (2;3) |
Б. (2;4) |
B. (3;4) |
Г. (–2;–4) |
|
2 + 3 = 5 |
2 + 4 = 6 |
3 + 4 = 7 |
–2 + (–4) = –6 |
Завдання 3
Укажіть пару чисел, що є розв'язком системи рівнянь x – y = 7, х + у = 1.
|
А. (4;3) |
Б. (–4;3) |
В. (–4;–3) |
Г. (4;–3) |
|
4 – 3 = 1 |
–4 – 3 = –7 |
–4 – (–3) = –1 |
4 – (–3) = 4 + 3 = 7 4 + (–3) = 4 – 3 = 1 |
Завдання 4
Розв'язком якого рівняння є пара чисел (2;–1) ?
|
A. x + 3y = 5 |
Б. 3x + y = 5 |
B. 2x + y = 5 |
Г. x + y = 3 |
|
2 + 3 • (–1) = –1 |
3 • 2 + (–1) = 5 |
2 • 2 + (–1) = 3 |
2 + (–1) = 1 |
Завдання 5 Розв'яжіть способом підстановки
{3х – у = 5
4x + 3у = 11
y = 3x – 5
Підставимо значення змінної у в рівняння 4х – 3у = 11:
4x + 3(3x – 5) = 11
4x + 9x – 15 = 11
13x = 26
x = 2
Підставимо знайдене значення змінної x у рівняння у = 3х – 5:
y = 3 • 2 – 5
у = 1
Відповідь: A. (2; 1).
Завдання 6 Розв'яжіть способом додавання
{4x – 7y = 11
3x + 7y = –4
7x = 7
x = 1
Підставимо знайдене значення змінної x у рівняння 4х – 7у = 11:
4 – 7y = 11
–7y = 7
y = –1
Відповідь: Г(1; –1).
Завдання 7
Серед розв'язків рівняння x + 2y = –18 знайдіть пару рівних між собою чисел.
A. (6;6), бо 6 + 2 • 6 = 6 + 12 = 18, 18 ≠ –18
Б. (–6 ;–6), бо –6 + 2 • (–6) = –6 + (–12) =–18
B. (0;0), бо 0 + 2 • 0 = 0, 0 ≠ –18
Г. (–9 ;–9), бо (–9) + 2 • (–9) = –9 + (–18) = –27, –27 ≠ –18
Завдання 8
Для якого значення m графік рівняння mx + 3y = 5 проходить через точку (–2 ;3)?
–2m + 3 • 3 = 5
–2m = 5 – 9
–2m = –4
m = 2
Відповідь: A. 2.
Завдання 9
З пунктів А і В, відстань між якими 60 км, вирушили одночасно пішохід і велосипедистка. Якщо вони рухатимуться назустріч одне одному, то зустрінуться через 3 год, а якщо вони рухатимуться в одному напрямку, то велосипедистка наздожене пішохода через 5 год. Знайдіть швидкість пішохода.
Розв'язання
Нехай швидкість пішохода дорівнює x км/год, а швидкість велосипедистки — y км/год.
|
|
|
Швидкість, км/год |
Час, год |
Відстань, км |
|
Назустріч
|
Пішохід |
х |
3 |
3х |
|
Велосипедистка |
у |
3 |
3у |
|
| У одному напрямку |
Пішохід |
х |
5 |
5х |
|
Велосипедистка |
у |
5 |
5у |
Складаємо систему рівнянь:
{3x + 3y = 60
5х + 60 = 5у
{3x + 3y = 60 |:3
5x – 5у = –60 |:5
{x + y = 20
x – у = –12
2х = 8
х = 4
Відповідь: Б. 4 км/год.
Завдання 10
Скільки є пар натуральних чисел, які є розв'язками рівняння 2x + y = 9?
2 • 1 + 7 = 9; 2 • 2 + 5 = 9; 2 • 3 + 3 = 9; 2 • 4 + 1 = 9
Відповідь: Б. чотири.
Завдання 11
Графік функції y = kx + b проходить через точки (1;4) і (–2;13). Знайдіть k.
{k + b = 4 |•(–1)
–2k + b = 13
{–k – b = –4
–2k + b = 13
–3k = 9
k = –3
Відповідь: B. –3.
Завданння 12
Для якого значення a система рівнянь 2х – Зу = 8, ax – 6y = 16 має безліч розв'язків?
{2х – Зу = 8 |•2
аx – 6y = 16
{4x – 6y = 1
аx – 6y = 16
Система має безліч розв'язків, якщо а = 4, тому A. 4
Завдання 13
Установіть відповідність між графіком рівняння (1–3) та точками перетину графіка з осями координат (А–Г).
|
Графік рівняння |
Точки перетину графіка з осями координат |
|
1. 2x – 5y = 10 2. 5x + 3y = 15 3. –3x + 4y = 12 |
A. (–4;0), (0;3) Б. (5;0), (0;3) B. (5;0), (0;–2) |
Відповідь: 1 — B; 2 — Г; 3 — A.
ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ ДО §§ 25–30
Завдання 1 Лінійним рівнянням з двома змінними
|
1) 2x + 3y = 9 |
2) 2x + 3y² = 9 |
Завдання 2
Чи є розв'язком рівняння 2x + y = 7 пара чисел:
1) (3;–5); Ні, бо 2 • 3 + (–5) = 6 – 5 = 1, 1 ≠ 7;
2) (4;–1). Так, бо 2 ∙ 4 + (–1) = 8 – 1 = 7.
Завдання 3
Чи є розв'язком системи x + у = 11, х – у = З пара чисел:
1) (6;5); Ні, бо 6 + 5 = 11, а 6 – 5 = 1;
2) (7;4)? Так, бо 7 + 4 = 11 і 7 – 4 = 3.
Завдання 4
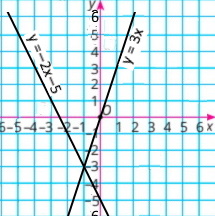
Розв'яжіть графічним способом систему рівнянь:
|
у = Зх |
2х + у = –5 |
Розв'язок системи рівнянь (–1;–3) |
|||||||||||
|
|
|
Завдання 5
Розв'яжіть способом підстановки систему рівнянь.
{x – 3у = 5
2x + y = 3
x = 3y + 5
Підставимо значення змінної х у рівняння 2х + у = 3:
2(3y + 5) + y = 3
6y + 10 + y = 3
7y = –7
y = –1
Підставимо знайдене значення змінної у в рівняння х = 3у + 5:
x = –3 + 5
х = 2
Відповідь: (2;–1)
Завдання 6
Розв'яжіть способом додавання систему рівнянь.
{5x + 3y = 3
4х - 3у = 24
9x = 27
x = 3
Підставимо знайдене значення змінної х у рівняння 5х + 3у = 3:
15 + 3y = 3
3y = –12
y = –4
Відповідь: (3;–4)
Завдання 7
{2(x + 3) = 7y – 5
6(x – 3) – 5(y + 1) = –24
{2x + 6 – 7y = –5
6x – 18 – 5y – 5 = –24
{2x – 7y = –11 |•(–3)
6x – 5y = –1
{–6x + 21y = 33
6х – 5y = –1
16y = 32
у = 2
Підставимо знайдене значення змінної у в рівняння 6х – 5у = –1:
6x – 5 • 2 = –1
6х – 10 = –1
–6x = –9
x = 1,5
Відповідь: (1,5;2)
Завдання 8
За 8 зошитів і 3 блокноти заплатили 93 грн. Після того як зошит подорожчав на 15%, а блокнот подешевшав на 10 %, за один зошит і один блокнот заплатили 20,4 грн. Якими були початкові ціни зошита і блокнота?
Розв'язання
Нехай початкова ціна зошита x грн, а блокнота - y. Після подорожчання на 15%, зошит коштував 1,15х грн, а після подешевшання на 10%, блокнот коштував 0,9у грн. Складаємо систему рівнянь:
{8x + 3y = 93 |•(–0,3)
1,15x + 0,9y = 20,4
{–2,4x – 0,9y = –27,9
1,15x + 0,9y = 20,4
1,25x = –7,5
x = 6
Підставимо знайдене значення змінної х у рівняння 8х + 3у = 93:
8 • 6 + 3у = 93
48 + 3у = 93
3у = 45
у = 15
Відповідь: ціна зошита 6 грн і ціна блокнота 15 грн.
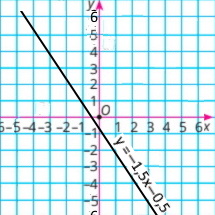
Завдання 9 Графік рівняння
|
(x + 2)/4 + (y – 3)/6 = –1/12 |•12 3(x + 2) + 2(y – 3) = –1 3x + 6 + 2y – 6 = –1 3x + 2y = –1 2у = –3х – 1 у = –1,5х – 0,5
|
|
Завдання 10
Графік функції y = kx + b проходить через точки (3;–4) і (–12;–9). Знайдіть k і b.
{3k + b = –4 |•(–1)
–12k + b = –9
b = –4 – 3k
Підставимо значення змінної b у рівняння 12k + b = –4:
–12k – 4 – 3k = –9
–15k = –5
k = 1/3
Підставимо значення змінної k у рівняння b = –4 – 3k:
b = –4 – 1
b = –5
Відповідь: k = 1/3; b = –5.
Завдання 11
{7х – ау = 5 |•3
21x + 6у = 15
{21х – 3ау = 15
21x + 6у = 15
Система має безліч розв'язків, якщо –3а = 6; а = –2.
Відповідь: а = –2.