Завдання 1
Перевірте, чи є число 7 коренем рівняння:
1) х – 2 = 5; Так, бо 7 – 2 = 5
2) 56 : х = 6. Ні, бо 56 : 7 = 8, 8 ≠ 6
Завдання 2
|
1) р4р3 = p7 |
2) t9 : t5 = t4 |
Завдання 3
Чи проходить графік рівняння х – у = 5 через точку:
|
1) М(6;2); Ні, бо 6 – 2 = 4 |
2) N(4;–1)? Так, бо 4 – (–1) = 5 |
Завдання 4 Спрощення виразів
1) (х – 3)(х + 3) – х(х – 5) = x² – 9 – x² + 5x = 5x – 9
2) (а + 2)² + (а – 7)(а + 3) = a² + 4a + 4 + a² – 4a – 21 = 2a² – 17
Завдання 5 Розкладання на множники
1) 14р3 – 21р2m = 7p²(2p – 3m)
2) За² – 12b² = 3(a² – 4b²) = 3(a – 2b)(a + 2b)
Завдання 6 Рівняння
5(х – 3) – 3(х + 2) = 3 – х
5x – 15 – 3x – 6 = 3 – x
3x = 24
x = 8
Завдання 7
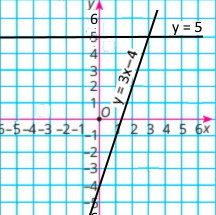
Побудуйте в одній системі координат графіки функцій y = 3х – 4 і y = 5 та знайдіть координати точки їх перетину.
|
y = 3х – 4 y = 5 |
|
Розв'язок (3;5) |
Завдання 8 Система рівнянь
{3х + 2у = 5 |•(–3)
–4х + 3y = 16 |•2
{–9x – 6y = –15
–8x + 6y = 32
–17x = 17
x = –1
–3 + 2y = 5
2y = 8
y = 4
Відповідь: (–1;4)
Завдання 9
З пункту А до пункту В вирушив пішохід. Через 1 год назустріч йому з пункту В виїхала велосипедистка. Відстань між пунктами А і В дорівнює 58 км, а швидкість велосипедистки на 10 км/год більша за швидкість пішохода. Знайдіть швидкість велосипедистки і швидкість пішохода, якщо вони зустрілися через 4 год після виходу пішохода.
Розв'язання
Нехай швидкість пішохода х км/год, тоді швидкість велосипедиста у км/год. За 4 год пішохід пройшов 4х км, а велосипедистка за 4 – 1 = 3 год проїхала 3у км. Складаємо систему рівнянь:
у – х = 10
4х + 3у = 58
х = у – 10
4(у – 10) + 3у = 58
Розв'язуєио рівняння:
4(у – 10) + 3у = 58
4у – 40 + 3у = 58
7у = 98
у = 14
х = 14 – 10 = 4
Відповідь: швидкість пішохода 4 км/год і швидкість велосипедистки 14 км/год.