До § 27 – 29
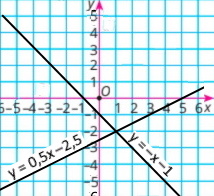
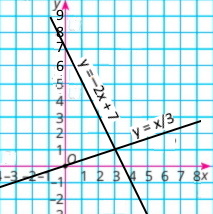
Завдання 1306 Розв'яжіть систему рівнянь трьома способами:
|
Графічний спосіб |
|||||||||||||||||||||||||||
|
1) {x – 2y = 5 x + y = –1 |
2) {2x + y = 7 –x + 3y = 0 |
||||||||||||||||||||||||||
|
у = 0,5х – 2,5
|
y = –х – 1
|
y = –2x + 7
|
y = х/3
|
||||||||||||||||||||||||
|
Відповідь: (1;–2) |
Відповідь: (3;1) |
||||||||||||||||||||||||||
|
Спосіб підстановки |
|||||||||||||||||||||||||||
|
{x – 2y = 5 x + y = –1 {x = 5 + 2y 5 + 2y + y = –1 Розв'язуємо рівняння: 5 + 2y + y = –1 5 + 3у = –1 3y = –6 y = –2 Підставляємо у в рівняння х = 5 + 2у: x = 5 + 2 • (–2) = 5 – 4 = 1 Відповідь: (1;–2) |
в) {2x + y = 7 –x + 3y = 0 {x = 3y 6y + y = 7 Розв'язуємо рівняння: 6y + y = 7 7y = 7 y = 1 Підставляємо у в рівняння х = 3у: x = 3 • 1 = 3 Відповідь: (3;1) |
||||||||||||||||||||||||||
|
Спосіб додавання |
|||||||||||||||||||||||||||
|
{x – 2y = 5 |•(–1) x + y = –1 {–x + 2y = –5 x + y = –1 3y = –6 y = –2 Підставляємо у в рівняння х + у = –1: x + (–2) = –1 х – 2 = –1 х = 1 Відповідь: (1;–2) |
б) {2x + y = 7 –x + 3y = 0 |•2 {2x + y = 7 –2x + 6y = 0 7y = 7 y = 1 Підставляємо у в рівняння 2х + у = 7: 2x + 1 = 7 2х = 6 х = 3 Відповідь: (3;1) |
||||||||||||||||||||||||||
Завдання 1307 Розв'язок системи рівнянь
|
1) {2 – 5х = 3(1 – у) 2(х + у) = 0,5х + 5,5 {2 – 5x = 3 – 3y 2x + 2y = 0,5x + 5,5 {3y – 5x = 1 |•(–2) 1,5x + 2y = 5,5 |•3 {10x – 6y = –2 4,5 + 6y = 16,5 14,5x = 14,5 x = 1 Підставляємо х у рівняння 10х – 6у = –2: 10 • 1 – 6y = –2 10 – 6y = –2 –6y = –12 y = 2 Відповідь: (1;2) |
2) {4(х + 7) – 9(у –13 ) = 139 5(х –1 ) + 4(3 – у) = –15 {4x + 28 – 9y + 117 = 139 5x – 5 + 12 – 4y = –15 {4x – 9y = –6 |•(–5) 5x – 4y = –22 |•4 {–20x + 45y = 30 20x – 16y = –88 29y = –58 y = –2 Підставляємо у в рівняння 4х – 9у = –6: 4x – 9 • (–2) = –6 4x + 18 = –6 4x = –24 x = –6 Відповідь: (–6;–2) |
Завдання 1308
|
1) {2/3 x – 4/5 y = 2 4/15 3/7 x + 2/5 y = –13/35 {2/3 x – 4/5 y = 34/15 |•15 3/7 x + 2/5 y = –13/35 |•35 {5 • 2x – 3 • 4y = 34 5 • 3x + 7 • 2y = –13 {10x – 12y = 34 |•(–1,5) 15x + 14y = –13 {–15x + 18y = –51 15x + 14y = –13 32y = –64 y = –2 Підставляємо у в рівняння 10х – 12у = 34: 10x – 12 • (–2) = 34 10x + 24 = 34 10x = 10 x = 1 Відповідь: (1;–2) |
2) {2/5 x – 1/4 y = 23/40 4/15 x – 3/5 y = 1 1/30 {2/5 х – 1/4 y = 23/40 |•40 4/15 х – 3/5 у = 31/30 |•30 {16x – 10y = 23 8x – 18y = 31 |•(–2) {16x – 10y = 23 –16x + 36y = –62 26y = –39 y = –1,5 Підставляємо у в рівняння 8х – 18у = 31: 8x – 18 • (–1,5) = 31 8x + 27 = 31 8x = 4 x = 0,5 Відповідь: (0,5;–1,5) |
Завдання 1309
|
1) {(x + 2)/3 + (y – 5)/3 = 2 |•3 (x + 2)/2 – (y – 5)/6 = 5/3 |•6 {x + 2 + y – 5 = 6 3(x + 2) – (y – 5) = 10 {x + y = 9 3x + 6 – y + 5 = 10 {x + y = 9 3x – y = 9 4x = 8 x = 2 Підставляємо у в рівняння х + у = 9: 2 + y = 9 y = 7 Відповідь: (2;7) |
2) {(2x + 1)/7 + (2y + 2)/5 = 1/5 |•35 (3x – 2)/2 + (y + 4)/4 = 4 |•4 {5(2x + 1) + 7(2y + 2) = 7 2(3x – 2) + y + 4 = 16 {10x + 5 + 14y + 14 = 7 6x – 4 + y + 4 = 16 {10x + 14y = –12 |:2 6x + y = 16 |•(–7) {5x + 7y = –6 –42x – 7y = –112 –37x = –118 x = 118/37 = 3 7/37 Підставляємо х у рівняння 6х + у = 16: 6 • 118/37 + y = 16 19 5/37 + у = 16 y = –3 5/37 Відповідь: (3 7/37;–3 5/37) |
Завдання 1310
Розв'яжіть систему рівнянь:
|
1) {2х + у = –2 –6х – 3у = 6 |:(–3) {2х + у = –2 2х + у = –2 Має безліч розв’язків виду (x;–2–2x) |
2) {х – 3у = 5 |•2 2х – 6у = 7 {2x – 6y = 10 2x – 6y = 7 Не має жодного розв’язку |
Завдання 1311
Чи має розв'язок система рівнянь:
|
1) {4х + 3у = 1 7х + 5у = 2 3х + 2у = 4 Розв’яжемо спочатку систему двох рівнянь, наприклад 1–го і 3–го, а потім перевіримо чи буде розв’язок розв’язком для 2–го рівняння. {4x + 3y = 1 |•(–2) 3x + 2y = 4 |•3 {–8x – 6y = –2 9x + 6y = 12 x = 10 Підставляємо х у рівняння 4х + 3у = 1: 4 • 10 + 3у = 1 40 + 3y = 1 3y = –39 y = –13 Підставимо (10;–13) в рівняння 7х + 5у = 2: 7 • 10 + 5 • (–13) = 70 – 65 = 5; 5 ≠ 2 Система немає розв’язку.
|
2) {3х – 4у = 10 4х + 7у = 1 5х + 6у = 4 Розв’яжемо спочатку систему двох рівнянь, наприклад 1–го і 2–го, а потім перевіримо чи буде розв’язок розв’язком для 3–го рівняння. {3x – 4y = 10 |•(–4) 4x + 7y = 1 |•3 {–12x + 16y = –40 12x + 21y = 3 37y = –37 y = –1 Підставляємо х у рівняння 3х – 4у = 10: 3х – 4 • (–1) = 10 3х + 4 = 10 3x = 6 x = 2 Підставимо (2;––1) в рівняння 5х + 6у = 4: 5 • 2 + 6 • (–1) = 10 – 6 = 4; 4 = 4 Розв’язок (2;–1) |
Завдання 1312
Графік функції y = kx + l перетинає вісь x у точці з абсцисою 4, а вісь y – у точці з ординатою –5 .
1) Задайте функцію формулою.
Якщо графік прямої y = kx + l проходить через точки (4;0) і (0;–5), то k і l повинні задовольняти систему:
{4k + l = 0
0k + l = –5
l = –5
Підставляємо х у рівняння 4k + l = 0:
4k – 5 = 0
4k = 5
k = 1,25
Формула функції: y = 1,25k – 5
2) Графік прямої y = 1,25x – 5 проходить через точку (–80;–105), бо
–105 = 1,25 • (–80) – 5; –105 = –105.
Завдання 1313
Розв'яжіть систему рівнянь:
|
1) |
2) |
|
{3(х – 2у) + х(7 – 2у) = 2у(1 – х) 4(х – у – 1) + 5(х + у – 1) = 32 {3x – 6y + 7x – 2xy = 2y – 2xy 4x – 4y – 4 + 5x + 5y – 5 = 32 {3x – 6y + 7x – 2xy – 2y + 2xy=0 4x – 4y + 5x + 5y = 32 + 4 + 5 {10x – 8y = 0 9x + y= 41 |•8 {10x – 8y = 0 72x + 8y = 328 82x = 328 x = 4 Підставляємо х у рівняння 10х – 8у = 0: 10 • 4 – 8у = 0 40 – 8y = 0 8y = 40 y = 5 Відповідь: (4;5) |
{(x + 2)² + (у – 1)² =(х + З)² +(у + 1)² (у – 2)² – (у + 2)² =(х + 6)² – (х – 1)² {x²+4x+ 4+y²–2y+1=x²+6x+9+y²+2y+1 y²–4y+4–y²–4y– 4=x²+12x+36–x²+2x–1 {x² + 4x + y² – 2y – x² – 6x – y² – 2y=5 y² – 4y – y² – 4y – x² – 12x + x² – 2x=35 {–2x – 4y = 5 |•(–2) –14x – 8y = 35 {4x + 8y = –10 –14x – 8y = 35 –10x = 25 x = –2,5 Підставляємо х у рівняння 4х + 8у = –10: 4 • (–2,5) + 8у = –10 –10 + 8y = –10 8y = 0 y = 0 Розв’язок (–2,5;0) |
Завдання 1314
Для якого значення а система рівнянь:
|
1) має безліч розв'язків |
2) не має розв'язків |
3) має єдиний розв'язок |
|
{5x + 4y = 2 |•2 10x + 8y = 4 {10x + 8y = 4 10x + 8y = a Безліч розв’язків, якщо a = 4 |
{5x + 4y = 2 |•2 10x + 8y = 4 {10x + 8y = 4 10x + 8y = a Не має розв’язків, якщо a ≠ 4 |
{5x + 4y = 2 |•2 10x + 8y = 4 {10x + 8y = 4 10x + 8y = a Має безліч розв’язків, якщо а = 4, або не має розв’язків, якщо а ≠ 4, тому не існує такого значення а, при якому є єдиний розв’язок. |
Завдання 1315
|
1) має безліч розв'язків |
2) має єдиний розв'язок |
|
{12x – 9y = 15 4x + by = 5 |•3 {12x – 9y = 15 12x + 3by = 15 Має безліч розв’язків, якщо 3b = –9; b = –3 |
{12x – 9y = 15 4x + by = 5 |•(–3); {12x – 9y = 15 –12x – 3by = –15 {–9y – 3by = 0 (–9 – 3b)y = 0 Має єдиний розв’язок, якщо b ≠ –3; Якщо y = 0; 12x = 15; x = 1,25 Розв'язок (1,25;0) |
До § 30
Завдання 1316
За 3 год автобусом і 5 год поїздом туристка подолала 450 км. Знайдіть швидкість автобуса і швидкість поїзда, якщо швидкість поїзда на 10 км/год більша за швидкість автобуса.
Розв'язання
Нехай швидкість автобуса дорівнює x км/год, а поїзда — y км/год. За 3 год автобусом і 5 год поїздом туристка подолає (3х + 5у) км або 450 км. За умовою швидкість поїзда на 10 км/год більша за швидкість автобуса, тобто у – х = 10 км/год. Складаємо систему рівнянь:
{3x + 5y = 450
y – x = 10
{3x + 5(х + 10) = 450
y = x + 10
Розв'язуємо рівняння:
3x + 5(х + 10) = 450
3x + 5х + 50 = 450
8х = 400
х = 50
Підставляємо х у рівняння у = х + 10:
у = 50 + 10 = 60
Відповідь: швидкість автобуса 50 км/год, потяга — 60 км/год.
Завдання 1317
За 7 порцій млинців і 2 салати заплатили 468 грн. Скільки коштує одна порція млинців і скільки – один салат, якщо дві порції млинців на 27 грн дешевші за три салати?
Розв'язання
Нехай порція млинців коштує x грн, а порція салату — у грн. Складаємо система рівнянь:
{7x + 2y = 468 |•(–3)
3y – 2x = 27 |•2
{–6y – 21x = –1404
6y – 4x = 54
–25x = –1350
x = 54
Підставляємо х у рівняння 3у – 2х = 27:
3y – 2 • 54 = 27
3y – 108 = 27
3y = 81
y = 27
Відповідь: порція млинців коштує 54 грн, а порція салату — 27 грн.
Завдання 1318
Теплохід за 3 год за течією і 2 год проти течії долає 142 км. Цей самий теплохід за 4 год проти течії долає на 14 км більше, ніж за 3 год за течією. Знайдіть власну швидкість теплохода і швидкість течії.
Розв'язання
Нехай власна швидкість теплохода x км/год, а швидкість течії — у км/год, тоді швидкість теплохода проти течії дорівнює (x – y) км/год, а за течією — (x + y) км/год. За 3 год за течією річки теплохід долає 3(х + у) км, за 2 год проти течії – 2(х + у) км, а разом 142 км. Відстань за 4 год проти течії 4(х – у) на 14 км більша, ніж за 3 год за течією 3(х + у). Складаємо систему рівнянь:
{3(x + y) + 2(x – y) = 142
4(x – y) – 3(x + y) = 14
{3x + 3y + 2x – 2y = 142
4x – 4y – 3x – 3y = 14
{5x + y = 142
x – 7y = 14 |•(–5)
{5x + y = 142
–5x + 35y = –70
36y = 72
y = 2
Підставляємо у в рівняння х – 7у = 14:
x – 7 • 2 = 14
х – 14 = 14
x = 28
Відповідь: швидкість теплохода 28 км/год, а швидкість течії – 2 км/год.
Завдання 1319
Майстер і його учень повинні були виготовити 114 деталей. Після того як учень пропрацював 2 год, до роботи приєднався майстер, і вони разом закінчили роботу за 3 год. Скільки деталей за годину виготовляв майстер і скільки учень, якщо майстер за 2 год виготовляє стільки само деталей, скільки учень за 3 год?
Розв'язання
Нехай майстер за 1 годину виготовив x деталей, а учень — у деталей. За 2 год майстер виготовив 2х деталей, а за 3 год учень – 3у деталей, причому їхня кількість однакова, тобто 2х = 3у. За 2 год учень виготовив 2у деталей, а за 3 год, працюючи разом, учень і майстер виготовлять 3(х + у) деталей або разом 114 деталей. Складаємо систему рівнянь:
{2y + 3(x + y) = 114
2x = 3y
{2y + 3x + 3y = 114
2x – 3y = 0
{3x + 5y = 114 |•(–2)
2x – 3y = 0 |•3
{–6x – 10y = –228
6x – 9y = 0
–19y = –228
y = 12
Підставляємо у в рівняння 2х – 3у = 0:
2x – 3 • 12 = 0
2х – 36 = 0
2х = 36
x = 18
Відповідь: майстер за 1 годину виготовив 18 деталей, а учень – 12 деталей.
Завдання 1320
Два ящики наповнено грушами. Якщо з другого ящика перекласти в перший 10 груш, то в обох ящиках груш стане порівну. Якщо з першого ящика перекласти в другий 44 груші, то груш у першому ящику залишиться в 4 рази менше, ніж у другому. Скільки груш у кожному ящику?
Розв'язання
Нехай у першому ящику було x груш, а в другому — у груш. Складаємо систему рівнянь:
{y – 10 = x + 10
y + 44 = 4(x – 44)
{y – x = 20
y + 44 = 4x – 176
{y – x = 20
–y + 4x = 220
3x = 240
x = 80
Підставляємо х у рівняння у – х = 20:
y – 80 = 20
y = 100
Відповідь: у першому ящику було 80 груш, а в другому — 100 груш.
Завдання 1321
Різниця між половиною одного числа і 0,75 другого дорівнює 8. Якщо перше число зменшити на його сьому частину, а друге збільшити на його дев'яту частину, то їх сума становитиме 100. Знайдіть ці числа.
Розв'язання
Нехай перше число дорівнює x, а друге число — у. Половина першого числа 0,5х і 0,75 другого 0,75у дорівнює 8. Перше число після зменшення дорівнює x – 1/7x = 6/7x, друге число після збільшення — (y + 1/9y) = 1 1/9y, а їхня сума 100. Складаємо систему рівнянь:
{0,5x – 0,75y = 8 |•4
6/7x + 1 1/9y = 100
{2x – 3y = 32 |•(–27)
6/7x + 10/9y = 100 |•63
{–54x + 81y = –864
54x + 70y = 6300
151y = 5436
y = 36
Підставляємо у в рівняння 2х – 3у = 32:
2x – 3 • 36 = 32
2x – 108 = 32
2x = 140
x = 70
Відповідь: перше число дорівнює 70, а друге — 36.
Завдання 1322
Сума трьох чисел, з яких друге в 5 разів більше за перше, дорівнює 140. Якщо друге число збільшити на 15 %, третє зменшити на 10 %, а перше число не змінювати, то сума цих чисел становитиме 139,5. Знайдіть ці числа.
Розв'язання
Нехай перше число дорівнює x, третє число — у, а друге число – 5х, а їхня сума х + у + 5х = 140 або 6х + у = 140. Якщо друге число збільшити на 15%, отримаємо 5х • 1,15 = 5,75х, а третє зменшити на 10%, отримаємо 0,9у, а сума трьох чисел чисел 5,75х + 0,9у + х = 139,5 або 6,75х + 0,9у = 139,5 Складаємо систему рівняння:
{6х + у = 140
6,75х + 0,9у = 139,5
{у = –6х + 140
6,75х + 0,9(–6х + 140) = 139,5
Розв'язуємо рівняння:
6,75х + 0,9(–6х + 140) = 139,5
6,75х – 5,4х + 126 = 139,5
1,35х = 139,5 – 126
1,35х = 13,5
х = 10
Підставляємо х у рівняння у = –6х + 140:
у = –6 • 10 + 140 = –60 + 140 = 80
5х = 5 • 10 = 50
Відповідь: перше число дорівнює 10, друге — 50, а третє – 80.
Завдання 1323
Периметр прямокутника на 154 см більший за одну з його сторін і на 140 см більший за другу. Знайдіть площу прямокутника.
Розв'язання
Нехай довжина прямокутника дорівнює x, а ширина — у. Складаємо систему рівнянь:
{2x + 2y – x = 154
2x + 2y – y = 140
{x + 2y = 154
2x + y = 140 |•(–2)
{x + 2y = 154
–4x – 2y = –280
–3x = –126
x = 42
Підставляємо х у рівняння х + 2у = 154:
42 + 2y = 154
2y = 112
y = 56
S = х • у = 42 • 56 = 2352 (см²) – площа прямокутника.
Відповідь: площа прямокутника 2352 см².
Завдання 1324
Сума цифр деякого двоцифрового числа дорівнює 8. Якщо його цифри поміняти місцями, то одержимо число, що на 18 більше за дане. Знайдіть це число.
Розв'язання
Нехай цифри двоцифрового числа х і у, тоді двоцифрове число дорівнює xy = 10x + y, а сума цифр x + y = 8. Якщо поміняти місцями цифри, то отримаємо число yx = 10y + x, а різниця 10y + x – 10x – y = 18; 9y – 9x = 18; y – x = 2. Складаємо систему рівнянь:
{y + x = 8
10y + x – (10x + y) = 18
{y + x = 8
9y – 9x = 18 |:9
{y + x = 8
y – x = 2
2у = 10
у = 5
Підставляємо у в рівняння у + х = 8:
5 + х = 8
х = 3
Відповідь: двоцифрове число 35.
Завдання 1325
У двох бідонах місткістю 20 л і 15 л уже є певна кількість молока. Якщо в більший бідон вщерть долити молока з меншого, то в меншому бідоні залишиться половина початкової кількості. Якщо в менший бідон долити вщерть молока з більшого, то в більшому залишиться 2/3 від початкової кількості. По скільки літрів молока в кожному бідоні?
Розв'язання
Нехай у меншому бідоні x л молока, а в більшому — y л молока. У більший бідон з меншого долили 1/2 л молока, у менший бідон з більшого (1 – 2/3)y = 1/3y л молока. Складаємо систему рівнянь:
{1/2x + y = 20 |•2
x + 1/3y = 15 |•(–6)
{x + 2y = 40
–6х – 2y = –90
–5x = –50
x = 10
Підставляємо у в рівняння х + 2у = 40:
10 + 2y = 40
2у = 30
y = 15
Відповідь: у меншому бідоні 10 л молока, а в більшому — 15 л молока.