ДІАГНОСТИЧНА РОБОТА 6
Система лінійних рівнянь з двома змінними
Варіант 1
Завдання 1 Яке з рівнянь є лінійним рівнянням з двома змінними?
|
А. 3х² – 4y = 5 |
Б. 3х – 4y² = 5 |
В. 3х – 4y = 5 |
Г. 3х – 4y = t |
Завдання 2
Яка з точок належить графіку рівняння х + у = 9?
6 + 3 = 9
|
А. (–6;–3) |
Б. (6;3) |
В. (7;3) |
Г. (1;9) |
Завдання 3
Яка з пар чисел є розв’язком системи рівнянь
{х – y = 5
х + у = 1
x = 5 + y
5 + y + y = 1
2y = –4
y = –2
x + (–2) = 1
х = 3
Відповідь: (3;–2)
|
А. (2;–3) |
Б. (6;1) |
В. (–2;3) |
Г. (3;–2) |
Завдання 4
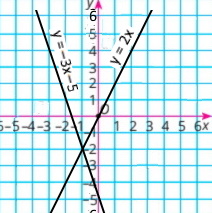
Розв’яжіть графічним способом систему рівнянь:
{у = 2х
3х + у = –5
|
у = 2х
|
у = –3х – 5
|
||||||||||||
|
Відповідь: (–1:–2) |
|||||||||||||
Завдання 5
Розв’яжіть систему рівнянь способом підстановки
{х – 2у = 5
4х + у = 2
{x = 5 + 2y
4(5 + 2y) + y = 2
Розв'язуємо рівняння:
4(5 + 2y) + y = 2
20 + 8y + y = 2
9y = –18
y = –2
Підставляємо знайдене значення змінної у в рівняння х = 5 + 2у:
x = 5 + 2 • (–2) = 5 – 4 = 1
ВІдповідь: (1;–2)
Завдання 6
Розв’яжіть систему рівнянь способом додавання
{3х + 4у = –14
5х – 4y = 30
8x = 16
x = 2
Підставляємо знайдене значення змінної х у рівняння 3х + 4у = –14:
3 • 2 + 4у = –14
6 + 4у = –14
4у = –20
у = –5
Відповідь: (2;–5)
Завдання 7
Для якого значення m графік рівняння mх + 2y = 18 проходить через точку (–2;6)?
–2m + 2 • 6 = 18
–2m = 6
m = –3
Відповідь: m = –3.
Завдання 8 Система рівнянь
{2(х – 4) = 7y – 25
6(х + 3) – 5(y + 2) = –11
{2x – 8 = 7y – 25
6x + 18 – 5y – 10 = –11
{2x – 7y = –17 |•(–3)
6x – 5y = –19
{–6x + 21y = 51
6x – 5y = –19
16y = 32
y = 2
Підставляємо знайдене значення змінної у в рівняння 2х – 7у = –17:
2х – 7 • 2 = –17
2х – 14 = –17
2х = –3
х = –1,5
Відповідь: (–1,5;2)
Завдання 9
За 7 зошитів і 3 ручки заплатили 176 грн. Після того як зошит подорожчав на 10 %, а ручка подешевшала на 15 %, за один зошит й одну ручку заплатили 32,2 грн. Якими були початкові ціни зошита та ручки?
Розв'язання
Нехай ціна одного зошита дорівнює x грн, а однієї ручки – y грн. Складаємо рівняння:
{7x + 3y = 176
1,1x + 0,85y = 32,2
{y = (176 – 7x)/3
1,1x + 0,85(176 – 7x)/3 = 32,2
Розв'язуємо рівняння:
1,1x + 0,85(176 – 7x)/3 = 32,2
1,1x + (149,6 – 5,95x)/3 = 32,2 |•3
3,3x + 149,6 – 5,95x = 96,6
–2,65x = –53
x = 20
Підставляємо знайдене значення змінної х у рівняння 7х + 3у = 176:
7 • 20 + 3у = 176
140 + 3у = 176
3у = 36
у = 12
Відповідь: ціна зошита 20 грн і ціна ручки 12 грн.
Варіант 2
Завдання 1
Яке з рівнянь є лінійним рівнянням з двома змінними?
|
А. 2х – 4у = z |
Б. 2х – 4y = 19 |
В. 2х – 4y² = 19 |
Г. 2х² – 4y = 19 |
Завдання 2
Яка з точок належить графіку рівняння х + у = 7?
5 + 2 = 7
|
А. (–5;–2) |
Б. (7;1) |
В. (5;2) |
Г. (5;3) |
Завдання 3
Яка з пар чисел є розв’язком системи рівнянь
{х + у = 9
х – у = –1
{x = 9 – y
9 – y – y = –1
Розв'язуємо рівняння:
9 – y – y = –1
–2y = –10
y = 5
Підставляємо знайдене значення змінної у в рівняння х = 9 – у:
x = 9 – 5 = 4
Відповідь: (4;5).
|
А. (4;5) |
Б. (5;4) |
В. (6;3) |
Г. (3;4) |
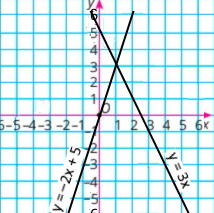
Завдання 4
Розв’яжіть графічним способом систему рівнянь:
{y = 3х
2х + у = 5
|
у = 3х
|
у = –2х + 5
|
||||||||||||
|
Відповідь: (1:3) |
|||||||||||||
Завдання 5
Розв’яжіть систему рівнянь способом підстановки
{х – 3y = 10
5х + у = 2
{x = 10 + 3y
5(10 + 3y) + y = 2
Розв'язуємо рівняння:
5(10 + 3y) + y = 2
50 + 15y + y = 2
16y = –48
y = –3
Підставляємо знайдене значення змінної у в рівняння х = 10 + 3у:
x = 10 + 3 • (–3) = 10 – 9 = 1
Відповідь: (1;–3)
Завдання 6
Розв’яжіть систему рівнянь способом додавання
{3х + 4y = –1
–3х + 7у = 23
11y = 22
y = 2
Підставляємо знайдене значення змінної у в рівняння 3х + 4у = –1:
3х + 4 • 2 = –1
3х + 8 = –1
3х = –9
х = –3
Відповідь: (–3;2)
Завдання 7
Для якого значення р графік рівняння 2х + ру = 12 проходить через точку (8;–2)?
2 • 8 – 2p = 12
–2p = –4
p = 2
Відповідь: р = 2.
Завдання 8
Розв’яжіть систему рівнянь
{5(x + 2) = 2у + 22
7(х – 4) – 6(у + 2) = –28
{5x + 10 = 2y + 22
7x – 28 – 6y – 12 = –28
{5x – 2y = 12 |•(–3)
7x – 6y = 12
{–15x + 6y = –36
7x – 6y = 12
–8x = –24
x = 3
Підставляємо знайдене значення змінної х у рівняння 7х – 6у = 12:
7 • 3 – 6у = 12
21 – 6у = 12
–6у = –9
у = 1,5
Відповідь: (3;1,5)
Завдання 9
За 3 ручки і 5 блокнотів заплатили 224 грн. Після того як ручка подорожчала на 20 %, а блокнот подешевшав на 5 %, за одну ручку й один блокнот заплатили 47,6 грн. Якими були початкові ціни ручки та блокнота?
Нехай ціна одного блокнота дорівнює x грн, а одної ручки – y грн. Складаємо рівняння:
{5x + 3y = 224
0,95x + 1,2y = 47,6
{y = (224 – 5x)/3
0,95x + 1,2(224 – 5x)/3 = 47,6
Розв'язуємо рівняння:
0,95x + 1,2(224 – 5x)/3 = 47,6
0,95x + (268,8 – 6x)/3 = 47,6 |•3
2,85x + 268,8 – 6x = 142,8
–3,15x = –126
x = 40
Підставляємо знайдене значення змінної х у рівняння у = (224 – 5х)/3:
y = (224 – 5 • 40)/3 = (224 – 200)/3 = 24/3 = 8
Відповідь: ціна ручки 40 грн і ціна блокнота 8 грн.
Варіант 3
Завдання 1
Яке з рівнянь є лінійним рівнянням з двома змінними?
|
А. 3х + 5у = 7 |
Б. 3х + 5у² = 7 |
В. 3х² + 5у = 7 |
Г. 3х + 5у = k |
Завдання 2
Яка з точок належить графіку рівняння х + у = 6?
4 + 2 = 6
|
А. (5;2) |
Б. (–4;–2) |
В. (6;1) |
Г. (4;2) |
Завдання 3
Яка з пар чисел є розв’язком системи рівнянь
{x – у = 9
х + у = 1
{x = 9 + y
9 + y + y = 1
2y = –8
y = –4
Підставляємо знайдене значення змінної у в рівняння х = 9 + у:
x = 9 + (–4) = 9 – 4 = 5
Відповідь: (5;–4).
|
А. (10;1) |
Б. (–4;5) |
В. (5;–4) |
Г. (–5;4) |
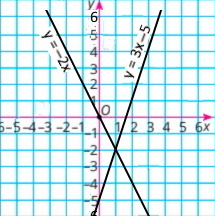
Завдання 4
Розв’яжіть систему рівнянь графічним способом
{у = –2х
–3х + у = –5
|
у = –2х
|
у = 3х – 5
|
||||||||||||
|
Відповідь: (1:–2) |
|||||||||||||
Завдання 5
Розв’яжіть систему рівнянь способом підстановки
{–2х + у = 4
х + 3у = 5
{x = 5 – 3y
–2(5 – 3y) + y = 4
Розв'язуємо рівняння:
–2(5 – 3y) + y = 4
–10 + 6y + y = 4
7y = 14
y = 2
Підставляємо знайдене значення змінної у в рівняння х = 5 – 3у:
х = 5 – 3 • 2 = 5 – 6 = –1
Відповідь: (–1;2)
Завдання 6
Розв’яжіть систему рівнянь способом додавання
{4х – 5у = 32
7х + 5у = 1
11x = 33
x = 3
Підставляємо знайдене значення змінної х у рівняння 7х+ 5у =1:
7 • 3 + 5у = 1
21 + 5у = 1
5у = –20
у = –4
Відповідь: (3;–4)
Завдання 7
Для якого значення m графік рівняння 4х + mу = –12 проходить через точку (2;–4)?
4 • 2 – 4m = –12
–4m = –20
m = 5
Відповідь: m = 5.
Завдання 8
Розв’яжіть систему рівнянь
{2(х – 3) = 5у + 17
8(х + 5) – 3(у + 1) = 61
{2x – 6 = 5y + 17
8x + 40 – 3y – 3 = 61
{2x – 5y = 23 |•4
8x – 3y = 24
{–8x + 20y = –92
8x – 3y = 24
17y = –68
y = –4
Підставляємо знайдене значення змінної х у рівняння 8х – 3у = 24:
8х – 3 • (–4) = 24
8х + 12 = 24
8х = 12
х = 1,5
Відповідь: (1,5;–4)
Завдання 9
За 5 ручок і 2 щоденники заплатили 170 гри. Після того як ручкa подешевшала на 15 %, а щоденник подорожчав на 10 % за одну ручку й один щоденник заплатили 82,1 грн. Якими були початкові ціни ручки та щоденника?
Розв'язання
Нехай ціна одного щоденника дорівнює x грн, а одної ручки – y грн. Складаємо рівняння:
{2x + 5y = 170
1,1x + 0,85y = 82,1
{y = (170 – 2x)/5
1,1x + 0,85(170 – 2x)/5 = 82,1
Розв'язуємо рівняння:
1,1x + 0,85(170 – 2x)/5 = 82,1
1,1x + (144,5 – 1,7x)/5 = 82,1 |•5
5,5x + 144,5 – 1,7x = 410,5
3,8x = 266
x = 70
Підставляємо знайдене значення змінної х у рівняння у = (170 – 2х)/5:
y = (170 – 2 • 70)/5 = (170 – 140)/5 = 30/5 = 6
Відповідь: ціна щоденника 70 грн і ціна ручки 6 грн.
Варіант 4
Завдання 1
Яке з рівнянь є лінійним рівнянням з двома змінними?
|
А. 7х – 5у = l |
Б. 7х – 5у² = 9 |
В. 7х² – 5у = 9 |
Г. 7х – 5у = 9 |
Завдання 2
Яка з точок належить графіку рівняння х + у = 8?
6 + 2 = 8
|
А. (6;2) |
Б. (–6;–2) |
В. (8;1) |
Г. (7;2) |
Завдання 3
Яка з пар чисел є розв’язком системи рівнянь
{х + у = 7
х – у = –1
{x = 7 – y
7 – y – y = –1
–2y = –8
y = 4
Підставляємо знайдене значення змінної у в рівняння х = 7 – у:
x = 7 – 4 = 3
Відповідь: (3;4)
|
А. (4;3) |
Б. (3;4) |
В. (2;5) |
Г. (3;–4) |
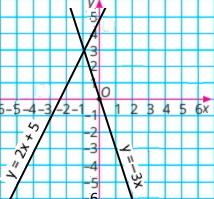
Завдання 4
Розв’яжіть систему рівнянь графічним способом
{у = –3х
–2х + у = 5
|
у = –3х
|
у = 2х + 5
|
||||||||||||
|
Відповідь: (–1:3) |
|||||||||||||
Завдання 5
Розв’яжіть систему рівнянь способом підстановки
{–2x – у = 5
х – 3у = 8
{x = 8 + 3y
–2(8 + 3y) – y = 5
Розв'язуємо рівняння:
–2(8 + 3y) – y = 5
–16 – 6y – y = 5
–7y = 21
y = –3
Підставляємо знайдене значення змінної у в рівняння х = 8 + 3у:
x = 8 + 3 • (–3) = 8 – 9 = –1
Завдання 6
Розв’яжіть систему рівнянь способом додавання
{–3х + 2у = 18
3х – 4у = –24
–2y = –6
y = 3
Підставляємо знайдене значення змінної у в рівняння 3х – 4у = –24:
3x – 4 • 3 = –24
3х – 12 = –24
3х = –12
х = –4
Завдання 7
Для якого значення р графік рівняння рх + 4у = –8 проходить через точку (4; 3)?
4p + 4 • 3 = –8
4p = –20
p = –5
Відповідь: p = –5
Завдання 8
Розв’яжіть систему рівнянь
{3(x – 5) = 8y + 9
7(х + 2) – 4(у + 5) = 28
{3x – 15 = 8y + 9
7x + 14 – 4y – 20 = 28
{3x – 8y = 24
7x – 4y = 34 |•(–2)
{3x – 8y = 24
–14x + 8y = –68
–11x = –44
x = 4
Підставляємо знайдене значення змінної х у рівняння 3х – 8у = 24:
3 • 4 - 8у = 24
12 - 8у = 24
-8у = 12
у = –1,5
Відповідь: (4;-1,5)
Завдання 9
За 5 зошитів і 3 блокноти заплатили 240 грн. Після того як зошит подешевшав на 5 %, а блокнот подорожчав на 20 %, за один зошит й один блокнот заплатили 83,4 грн. Якими були початкові ціни зошита та блокнота?
Розв'язання
Нехай ціна одного зошита – x грн, а одного блокноту – y грн. Складаємо рівняння:
{5x + 3y = 240
0,95x + 1,2y = 83,4
{y = (240 – 5x)/3
0,95x + 1,2(240 – 5x)/3 = 83,4
Розв'язуємо рівняння:
0,95x + 1,2(240 – 5x)/3 = 83,4
0,95x + (288 – 6x)/3 = 83,4 |•3
2,85x + 288 – 6x = 250,2
–3,15x = –37,8
x = 12
Підставляємо знайдене значення змінної х у рівняння у = (240 - 5з)/3:
y = (240 – 5 • 12)/3 =(240 - 60)/3 = 180/3 = 60
Відповідь: зіна зошита 12 грн і ціна блокнота 60 грн.