ДІАГНОСТИЧНА РОБОТА 5
Функції
Варіант 1
Завдання 1 Укажіть запис, що задає функцію.
|
А. 4 + 3х = 3х – 7 |
Б. 12 : 2 – 6 = 0 |
В. y = (x – 2)/7 |
Г. 7b – 2 < 5 |
Завдання 2 Лінійна функція
Загальна формула лінійної функції y = kx + l, де k, l – довільні числа
|
А y = 1/(2x + 3) |
Б. у = 2х + 3 |
В. у = х² + 3 |
Г. у = х² + 3х |
Завдання 3
Лінійну функцію задано формулою у = 5 – 2х. Укажіть коефіцієнти k і l цієї функції.
Загальна формула лінійної функції y = kx + l. Оскільки у = –2х + 5, то k = –2, l = 5
|
А. k = 5, l = –2 |
Б. k = 5, l = 2 |
В. k = 2, l = 5 |
Г. k = –2, l = 5 |
Завдання 4
Функцію задано формулою у = –3х + 5. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 4;
Якщо х = 4, то y = –3 • 4 + 5 = –12 + 5 = –7
2) значення аргументу, для якого значення функції дорівнює 8.
Якщо у = 8, то 8 = –3x + 5; –3x = 3; x = –1
Завдання 5
функцію задано формулою у = 0,7х – 6,3. Не виконуючи побудови:
1) знайдіть нулі функції;
Якщо у = 0, то 0,7x – 6,3 = 0; 0,7x = 6,3; x = 9. Нулі функції: (9;0)
2) з’ясуйте, чи проходить графік функції через точку М(10;0,5).
Якщо х = 10, то у = 0,7 • 10 – 6,3 = 0,7, 0,7 ≠ 0,5
Точка М(10;0,5) не проходить через графік функції у = 0,7х – 6,3.
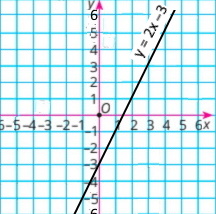
Завдання 6 Графік функції
|
у = 2х – 3
|
|
Користуючися графіком, знайдіть:
1) значення функції для х = 3; y = 3
2) значення аргументу, для якого у = –1. x = 1
Завдання 7
Знайдіть область визначення функції у = 3/(4x – x²).
4x – x² = 0
x(4 – x) = 0
x = 0 або 4 – x = 0
x = 0 або x = 4
Область визначення функції: усі дійсні числа, окрім 0 та 4.
Завдання 8
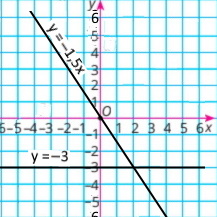
Побудуйте в одній системі координат графіки функцій у = –1,5х та у = –3 і знайдіть координати точки їх перетину.
|
у = –1,5х
|
Координати точки перетину: (2;–3) |
Завдання 9
Знайдіть найменше значення функції у = х² + 4х – 5.
y = х² + 4х – 5 = (x² + 4x + 4) – 9 = (x + 2)² – 9;
При x = –2 значення функції набуває найменше значення: –9.
Варіант 2
Завдання 1 Функція
|
А. 2а – 7 > 11 |
Б. у = (x + 9)/7 |
В. 7 + 2х = 2х – 3 |
Г. 14 : 2 – 6 = 1 |
Завдання 2 Лінійна функція
Загальна формула лінійної функції y = kx + l, де k, l – довільні числа
|
А. у = х² + 5х |
Б. у = х² + 5 |
В. y = 2х + 5 |
Г. y = 1/(2x + 5) |
Завдання 3
Лінійну функцію задано формулою у = 9 – 4х. Укажіть коефіцієнти k і І цієї функції.
Загальна формула лінійної функції y = kx + l. Оскільки у = –4х + 9, то k = –4, l = 9
|
A. k = –4, l = 9 |
Б. k = 4, l = 9 |
В. k = 9, l = –4 |
Г. k = 9, l = 4 |
Завдання 4
Функцію задано формулою у = 2х – 7. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 5;
Якщо х = 5, то у = 2 • 5 – 7 = 10 – 7 = 3
2) значення аргументу, для якого значення функції дорівнює –11.
Якщо у = –11, то –11 = 2x – 7; 2x = –4; x = –2
Завдання 5
Функцію задано формулою у = 0,4х – 3,6. Не виконуючи побудови:
1) знайдіть нулі функції;
яущо у = 0, то 0,4x – 3,6 = 0; 0,4x = 3,6; x = 9. Нулі функції: (9;0)
2) з’ясуйте, чи проходить графік функції через точку В(10;0,6).
Якщо х = 10, то у = 0,4 • 10 – 3,6 = 0,4, 0,4 ≠ 0,6
Точка В(10;0,6) не проходить через графік функції у = 0,4х – 3,6.
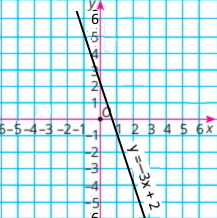
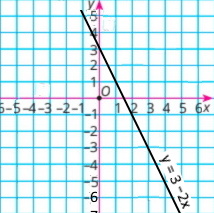
Завдання 6 Графік функції
|
у = –3x + 2
|
|
Користуючися графіком, знайдіть:
1) значення функції для х = 2; y = –4
2) значення аргументу, для якого у = 5. x = –1
Завдання 7
Знайдіть область визначення функції у = 7/(х² + 2х).
x² + 2x = 0
x(x + 2) = 0
x = 0 або x + 2 = 0
x = 0 або x = –2
Область визначення функції: усі дійсні числа, окрім 0 та –2.
Завдання 8
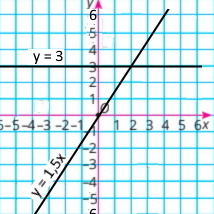
Побудуйте в одній системі координат графіки функцій у = 1,5х та у = 3 і знайдіть координати точки їх перетину.
|
у = 1,5х
|
Координати точки перетину: (2;3) |
Завдання 9
Знайдіть найменше значення функції у = х² – 4х + 3.
y = х² – 4х + 3 = (x² – 2x + 4) – 1 = (x – 2)² – 1;
При x = 2 значення функції набуває найменше значення: –1.
Варіант З
Завдання 1 Функція
|
А. 12 : 2 – 3 = 3 |
Б. 4х – 7 = 2 + 4х |
В. 3c – 2 > 7 |
Г. y = (x – 7)/11 |
Завдання 2 Лінійна функція
Загальна формула лінійної функції y = kx + l, де k, l – довільні числа
|
А. y = 1/(3x – 7) |
Б. у = 3х – 7 |
В. у = х3 – 7 |
Г. у = х3 – 7х |
Завдання 3
Лінійну функцію задано формулою у = 4 – 3x. Укажіть коефіцієнти k і І цієї функції.
Загальна формула лінійної функції y = kx + l. Оскільки у = –3х + 4, то k = –3, l = 4
|
A. k = –3, l = –4 |
Б. k = 3, l = 4 |
В. k = –3, l = 4 |
Г. k = 4, l = –3 |
Завдання 4
Функцію задано формулою у = –4х + 5. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 4;
Якщо х = 4, то у = –4 • 4 + 5 = –16 + 5 = –11
2) значення аргументу, для якого значення функції дорівнює 9.
Якщо у = 9, то 9 = –4x + 5; –4x = 4; x = –1
Завдання 5
Функцію задано формулою у = 0,6х – 4,2. Не виконуючи побудови:
1) знайдіть нулі функції;
Якщо у = 0, то 0,6x – 4,2 = 0; 0,6x = 4,2; x = 7. Нулі функції: (7;0)
2) з’ясуйте, чи проходить графік функції через точку А(10;1,5).
Якщо х = 10, то у = 0,6 • 10 – 4,2 = 1,8, 1,8 ≠ 1,5
Точка А(10;1,5) не проходить через графік функції у = 0,6х – 4,2.
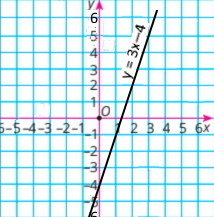
Завдання 6 Графік функції
|
у = 3x – 4
|
|
Користуючися графіком, знайдіть:
1) значення функції для х = 3; y = 5
2) значення аргументу, для якого у = –1. x = 1
Завдання 7
Знайдіть область визначення функції у = 5/(3x + x²).
3x + x² = 0
x(3 + x) = 0
x = 0 або 3 + x = 0
x = 0 або x = –3
Область визначення функції: усі дійсні числа, окрім 0 та –3.
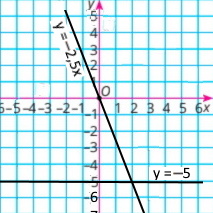
Завдання 8
Побудуйте в одній системі координат графіки функцій у = –2,5х та у = –5 і знайдіть координати точки їх перетину.
|
у = –2,5х
|
Координати точки перетину: (2;–5) |
Завдання 9
Знайдіть найменше значення функції у = х² + 8х + 13.
y = х² + 8х + 13 = (x² + 8x + 16) – 3 = (x + 4)² – 3;
При x = –4 значення функції набуває найменше значення: –3.
Варіант 4
Завдання 1 Функція
|
А. y = (x + 9)/11 |
Б. 2t – 5 < 7 |
В. 20 : 2 – 10 = 0 |
Г. 7х + 3 = 5 + 7х |
Завдання 2 Лінійна функція
|
А. у = 1/(2x – 7) |
Б. у = х² – 7х |
В. у = х² – 7 |
Г. у = 2х – 7 |
Завдання 3
Лінійну функцію задано формулою у = 7 – 5х. Укажіть коефіцієнти k і І цієї функції.
Загальна формула лінійної функції y = kx + l. Оскільки у = –5х + 7, то k = –5, l = 7
|
А. k = 5, l = 7 |
Б. k = –5, l = 7 |
B. k = –5, l = –7 |
Г. k = 7, l = –5 |
Завдання 4
Функцію задано формулою у = 3х – 4. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 4;
Якщо х = 4, то y = –3 • 4 – 4 = –12 – 4 = –16
2) значення аргументу, для якого значення функції дорівнює –13.
Якщо у = –13, то –13 = –3x – 4; –3x = –9; x = 3
Завдання 5
Функцію задано формулою у = 0,8х – 3,2. Не виконуючи побудови:
1) знайдіть нулі функції;
Якщо у = 0, то 0,8x – 3,2 = 0; 0,8x = 3,2; x = 4. Нулі функції: (4;0)
2) з’ясуйте, чи проходить графік функції через точку K(10;4,5).
Якщо у = 10, то 0,8 • 10 – 3,2 = 8 – 3,2 = 4,8, 4,8 ≠ 4,5
Точка K(10;4,5) не проходить через графік функції у = 0,8х – 3,2.
Завдання 6 Графік функції
|
у = –2х + 3
|
|
Користуючися графіком, знайдіть:
1) значення функції для х = –1; y = 5
2) значення аргументу, для якого у = 1. x = 1
Завдання 7
Знайдіть область визначення функції у = 4/(x² – 5x).
x² – 5x = 0
x(x – 5) = 0
x = 0 або x – 5 = 0
x = 0 або x = 5
Область визначення функції: усі дійсні числа, окрім 0 та 5.
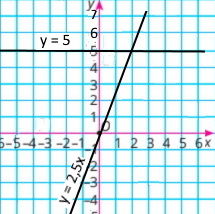
Завдання 8
Побудуйте в одній системі координат графіки функцій y = 2,5х та у = 5 і знайдіть координати точки їх перетину.
|
у = 2,5х
|
Координати точки перетину: (2;5) |
Завдання 9
Знайдіть найменше значення функції у = х² – 6х + 7.
y = х² – 6х + 7 = (x² – x + 9) – 2 = (x – 3)² – 2;
При x = 3 значення функції набуває найменше значення: –2.