ГДЗ Істер Алгебра 7 клас Завдання 1163 – 1192 § 27 Система двох лінійних рівнянь з двома змінними та її розв'язок. Розв'язування систем лінійних рівнянь з двома змінними графічно ВІДПОВІДІ

Інша завдання дивись тут...

Завдання 1163 Система двох лінійних рівнянь з двома змінними

1) {х + у = З

х – у² = 9

2) {Зх + 2y = 5

7x – 4y = 3

3) {2х – у = 9

xу = 5

4) {x/y = 2

x – y = 9

Завдання 1164

Чи є розв'язком системи рівнянь пара чисел:

1) (3;4)	2) (4;3)	3) (6;1)
1) {х + у = 7 х – у = 1 {3 + 4 = 7 3 – 4 = –1 Не є розв’язком	2) {х + у = 7 х – у = 1 {4 + 3 = 7 4 – 3 = 1 Є розв’язком	3) {х + у = 7 х – у = 1 {6 + 1 = 7 6 – 1 = 5 Не є розв’язком

Завдання 1165

Яка з даних пар чисел є розв'язком системи:

1) (5;0)	2) (2;3)	3) (3;2)
1) {х + у = 5 х – у = 1 {5 + 0 = 5 5 – 0 = 5 Не є розв’язком	2) {х + у = 5 х – у = 1 {2 + 3 = 5 2 – 3 = –1 Не є розв’язком	3) {х + у = 5 х – у = 1 {3 + 2 = 5 3 – 2 = 1 Є розв’язком

Завдання 1166

Скільки розв'язків має система, графіки рівнянь якої зображено:

на малюнку 27,4	на малюнку 27,5
Єдиний розв’язок пара чисел (–2;1)	Жодного розв’язку, бо графіки рівнянь паралельні

Завдання 1167

Чи є пара чисел (–2; 1) розв'язком системи:

1) {х + 2у = 0

Зx – 7у = –13

{–2 + 2 • 1 = 0

3 • (–2) – 7 • 1 = –13

Є розв’язком

2) {5х + 7у = –З

9x – 11у = 29

{5 • (–2) + 7 • 1 = –3

9 • (–2) – 11 • 1 = –29

Не є розв’язком

3) {2х = 5 – 9у

7у – 12х = 31

{2 • (–2) = 5 – 9 • 1

7 • 1 – 12 • (–2) = 31

Є розв’язком

Завдання 1168

Яка з пар є розв'язком системи?

1) {2х – Зy = 17

5х + 2у = 14

(3;–4)

2 • 3 – 3 • (–4) = 18 Не є розв’язком

(7;2)

2 • 7 – 3 • 2 = 8 Не є розв’язком

(4;–3)

{2 • 4 – 3 • ( –3) = 17

5 • 4 + 2 • (–3) = 14 Є розв’язком

2) {2х – 7у = 0

Зx + 5у = 31

(3;–4)

2 • 3 – 7 • (–4) = –22 Не є розв’язком

(7; 2)

{2 • 7 – 7 • 2 = 0

3 • 7 + 5 • 2 = 31 Є розв’язком

(4;–3)

2 • 4 – 7 • ( –3) = 29 Не є розв’язком

Завдання 1169

Складіть систему лінійних рівнянь з двома змінними, розв'язком якої є пара чисел:

1) (1;–3)	2) (4;5)
{3x + 2y = –3 5x – y = 8 бо 3 • 1 + 2 • (–3) = 3 – 6 = –3 5 • 1 – (–3) = 5 + 3 = 8	{3x + 2y = 22 5x – y = 15 бо 3 • 4 + 2 • 5 = 12 + 10 = 22 5 • 4 – 5 = 20 – 5 = 15

Завдання 1170

Знайдіть координати точки перетину прямих, які зображено на малюнку 27.6. Запишіть відповідну цим прямим систему рівнянь. Перевірте розв'язок, підставивши координати знайденої точки в кожне з рівнянь.

Координати точки перетину прямих x + y = 1 і 2x – y = –4 дорівнюють (–1;2) і є розв’язком системи:

{x + y = 1

2x – y = –4

Перевірка:

–1 + 2 = 1
2 • (–1) – 2 = –2 – 2 = –4

Пара чисел (–1;2) є розв’язком системи рівнянь.

Завдання 1171

Розв'яжіть графічно систему рівнянь:

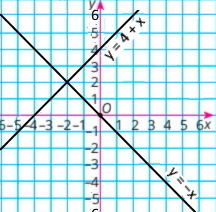
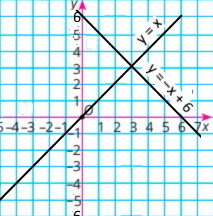
1) {y = –x

y = 4 + x

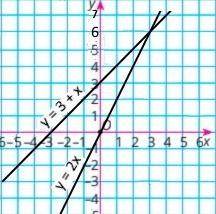
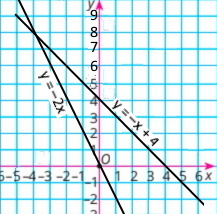
2) {y = 2x

y = 3 + x

у = –x

х	–1	1
у	1	–1

y = х + 4

х	0	1
у	4	5

y = 2x

х	–2	2
у	–4	4

y = х + 3

х	0	–1
у	3	2

Розв'язок системи рівнянь (–2;2)

Розв'язок системи рівнянь(3;6)

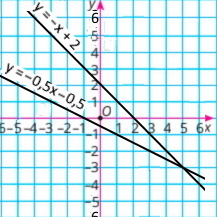
3) {x + y = 2

x + 2y = –1

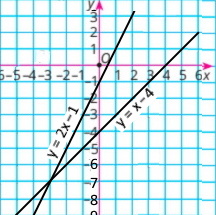
4) {2x – y = 1

x – y = 4

y = –х + 2

х	–2	2
у	4	0

y = –0,5х –0,5

х	0	3
у	–0,5	–2

у = 2x – 1

х	0	1
у	–1	1

у = x – 4

х	0	2
у	–4	–2

Розв'язок системи рівнянь (5;–3)

Розв'язок системи рівнянь (–3;–7)

Завдання 1172

Розв'яжіть графічно систему рівнянь:

1) y = x

y = 6 – x

2) y = –2x

y = 4 – x

y = x

х	–1	1
у	–1	1

y = –x + 6

х	0	1
у	6	7

y = –2x

х	–1	1
у	2	–2

y = –x + 4

х	0	–1
у	4	3

Розв'язок системи рівнянь (3;3)

Розв'язок системи рівнянь (–3;8)

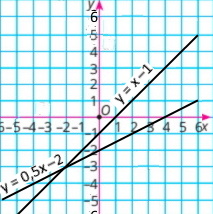
3) x – y = 1

x – 2y = 4

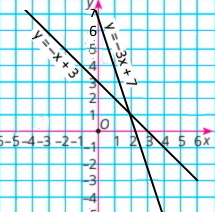
4) 3x + y = 7

x + y = 3

у = x – 1

х	0	1
у	–1	0

у = 0,5x – 2

х	0	2
у	–2	–1

у = –3x + 7

х	0	1
у	7	4

y = –x + 3

х	0	1
у	3	2

Розв'язок системи рівнянь (–2;–3)

Розв'язок системи рівнянь (2;1)

Завдання 1173, 1174

Пара (2;–5) є розв'язком системи, знайдіть значення а	Пара (10;–2) є розв'язком системи, знайдіть значення b
{2x + by = 5 ax – 6y = 13 {2 • 2 + b • (–5) = 5 2a – 6 • (–5) = 13 {4 – 5b = 5 2a + 30 = 13 {b = –0,2 a = –8,5	{ах – 5у = 17 Зх + by = 9 {a • 10 – 5 • (–2) = 17 3 • 10 + b • (–2) = 9 {10a + 10 = 17 30 – 2b = 9 {10a = 7 2b = 21 {a = 0,7 b = 10,5

Завдання 1175

Розв'яжіть графічно систему рівнянь:

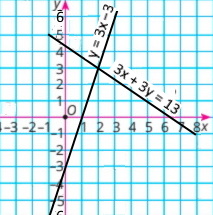
1) 2х + 3у = 13

Зх – у = 3

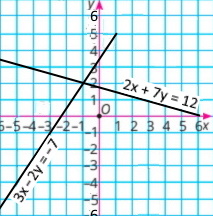
2) 2х + 7у = 12

Зх – 2у = –7

у = (13–2х)/3

х	2	5
у	3	1

у = Зх – 3

х	0	1
у	–3	0

у = (12 – 2х)/7

х	–1	–4,5
у	2	3

у = (3х + 7)/2

х	–1	1
у	2	5

Розв'язок системи рівнянь (2;3)

Розв'язок системи рівнянь (–1;2)

Завдання 1176

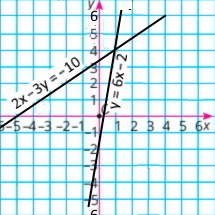
1) 2х – 3у = –10

6х – у = 2

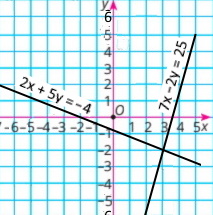
2) 2х + 5y = –4

7х – 2у = 25

у = (2х + 10)/3

х	1	–2
у	4	2

у = 6х – 2

х	0	1
у	–2	4

y = –0,4х – 0,8

х	–2	–1
у	0	–2

у = 3,5х – 12,5

х	–2	–1
у	0	–2

Розв'язок системи рівнянь (1;4)

Розв'язок системи рівнянь (–1;2)

Завдання 1177

З'ясуйте, чи має система розв'язки і скільки:

1) {2x – y = 5 3x + y = 7 5x = 12 x = 2,4 y = 7 – 3x = 7 – 3 • 2,4 = –0,2 Має один розв’язок (2,4;–0,2)	2) {0,5x – y = 4 \|•(–2) –x + 2y = –8 {–x + 2y = –8 –x + 2y = –8 Має безліч розв’язків (х;0,5х–4)
3) {x + 5y = 7 y = –0,2x {x + 5y = 7, 0,2x + y = 0 \|•5 {x + 5y = 7 x + 5y = 0 Не має розв’язку	4) {x + 2y = 0 2x + y = 0 x = –2y 2 • (–2y) + y = 0 –3y = 0 y = 0 x = 0 Має один розв’язок (0;0)

Завдання 1178

Чи має система розв'язки і скільки:

1) {x + y = 7

3x – y = 0

x + y + 3x – y = 7 + 0

4x = 7

x = 1,75

y = 7 – x = 7 – 1,75 = 5,25

Має один розв’язок

(1,75;5,25)

2) {x – 2y = 5 |•2

2x – 4y = 7

{2x – 4y = 10

2x – 4y = 7

Не має розв’язку

3) {x = 2y

1,5x – 3y = 0

{x – 2y = 0 |•1,5

1,5 – 3y = 0

{1,5x – 3y = 0

1,5x – 3y = 0

Має безліч розв’язків

(х;0,5х)

Завдання 1179

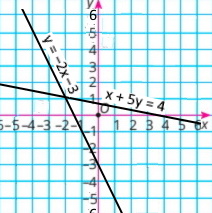
Розв'яжіть графічно систему рівнянь 2x + y = –3 і x + 5y = 4.

2x + y = –3

y = –2х –3

x + 5y = 4

у = –0,2х + 0,8

х	0	1
у	–3	–5

х	–1	9
у	1	–1

Одержаний розв'язок не є точним, адже графічний спосіб зазвичай дає змогу знаходити розв'язки лише наближено. Прямі перетинаються в точці, координати якої не є цілими числами.

Чи є розв'язком даної системи пара чисел (–2 1/9;1 2/9)?

{2x + y = –3

x + 5y = 4

2 • (–2 1/9) + 1 2/9 = 2 • (–19/9) + 11/9 = –38/9 + 11/9 = –27/9 = –3

(–2 1/9) + 5 • 1 2/9 = (–19/9) + 5 • 11/9) = –19/9 + 55/9 = 36/9 = 4

Пара чисел (–2 1/9;1 2/9) є розв'язком системи рівнянь.

Завдання 1180

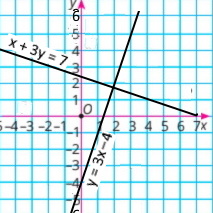
Розв'яжіть графічно систему рівнянь x + 3y = 7, 3x – y = 4.

x + 3y = 7

y = (–х + 7)/3

3x – y = 4

у = 3х – 4

х	–2	4
у	3	1

х	0	2
у	–4	2

Перевірте, чи є одержаний розв'язок точним. Ні, не є точним, адже графічний спосіб зазвичай дає змогу знаходити розв'язки лише наближено. Прямі перетинаються в точці, координати якої не є цілими числами.

Чи є розв'язком даної системи пара чисел (1,9; 1,7)?

{x + 3y = 7

3x – y = 4

1,9 + 3 • 1,7 = 1,9 + 5,1 = 7

3 • 1,9 – 1,7 = 5,7 – 1,7 = 4

Пара чисел (1,9;1,7) є розв'язком системи рівнянь.

Завдання 1181, 1182

Доведіть, що система рівнянь не має розв'язків.	Доведіть, що система рівнянь має безліч розв'язків.
{x – 7у = 8 \|•(–4) –4х + 28у = –31 {–4x + 28y = –32 –4x + 28y = –31 Не має розв'язків, бо не існує х і у, для яких би одночасно виконувалися дві різні рівності	{2х + 5у = 18 –3x – 7,5y = –27 {2х + 5у = 18 \|•(–1,5) –3x – 7,5y = –27 {–3 – 7,5y = –27 –3x – 7,5y = –27 Має безліч розв'язків (х;–0,4х+3,6)

Завдання 1183

Знайдіть які–небудь розв'язки системи Зх + у = 5, –9х – Зу = –15. Скільки всього розв'язків вона має? Розв'яжіть її.

{Зх + у = 5 |•(–3)

–9х – Зу = –15

{–9x – 3y = –15

–9x – 3y = –15

Має безліч розв'язків (х;5–3х).

Якщо х = 0, то у = 5, тому розв'язком може бути пара значень змінних (0:5)

Якщо х = 1, то у = –1, тому розв'язком може бути пара значень змінних (1:–1)

Завдання 1184 Розв'язання системи рівнянь

1) {Зх – 2у = 5

–6х + 4у = –10 |:(–2)

{3x – 2y = 5

3x – 2y = 5

Має безліч розв'язків (х;(1,5х–2,5)

2) {х + 3у = –4

Зх + 9у = 12 |:3

{x + 3y = –4

x + 3y = 4

Не має розв'язків

Завдання 1185

До рівняння x + 3y = 5 доберіть друге рівняння так, щоб одержана система рівнянь мала:

1) лише один розв'язок; 4x + y = 9

2) безліч розв'язків. 2x + 6y = 10

Завдання 1186

До рівняння 2x – y = 7 доберіть друге рівняння так, щоб одержана система рівнянь не мала розв'язків. 4x – 2y = 13.

Завдання 1187

Які з точок А(4;–2); Б(0;0); C(–1;–5); D(1;2) належать графіку прямої пропорційності:

1) y = –0,5x	2) y = 5x
точка А (4;–2) –2 = –0,5 • 4 –2 = –2 точка В (0;0) 0 = –0,5 • 0 0 = 0	точка В(0;0) 0 = 5 • 0 0 = 0

Завдання 1188 Спростіть вираз

1) 7m(m – 3) – 3(m – 2)(m + 2) = 7m² – 21m – 3m² + 12 = 4m² – 21m + 12

2) (1 – 2х)(2x + 1) – (Зx – 1)² = 1 – 4х² – 9х² + 6х – 1 = –13x² + 6х

3) (2х + 3у)² – (х + Зу)(2х – у) = 4х² + 12ху + 9у² – 2х² + ху – 6ху + Зу² = 2х² + 7xy + 12у²

4) (4а – 5b)(5b + 4а) – (2а – 5b)² = 16а² – 25b² – 4а² + 20аb – 25b² = 12а² + 20ab – 50b²

Завдання 1189

Доведіть, що вираз –x² + 8x – 17 для будь–яких значень x набуває лише від'ємних значень. Якого найбільшого значення набуває цей вираз і для якого значення x?

Вираз –x² + 8x – 17 = –((х² – 8х + 16) +1) = –((х – 4)² + 1) = –(х – 4)² – 1— набуває лише від’ємних значень. Найбільшого значення –1 вираз набуває, коли х – 4 = 0 при х = 4.

Завдання 1190

Тариф на послуги таксі в одній з компаній–перевізників формується так: пасажир сплачує по 6 грн за кожний кілометр шляху та додатково 30 грн за приїзд машини. Задайте формулою залежність витрат p (у грн) на одну поїздку від довжини шляху s (у км). p = 6s + 30

Завдання 1191

Виразіть з рівняння змінну у через х або х через у:

1) x – 4y = –5

x = 4у – 5

або

y = (x + 5)/4

2) 8x – y = 1

x = (у + 1)/8

або

y = 8x – 1

3) 2x – 3y = 5

x = (3у + 5)/2