МНОЖЕННЯ І ДІЛЕННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ ЧИСЛО
До № 531-549
Завдання 1. Обчисли зручним способом.
2 • 386 • 5 • 10 = 2 • 5 • 10 • 386 = 100 • 386 = 38 600
2356 • 4 • 25 : 10 = 2356 • 100 : 10 = 2356 • 10 = 23 560
245 • 3 + 7 • 245 = 245 • (3 + 7) = 245 • 10 = 2 450
Завдання 2. Туристи спочатку їхали 2 год поїздом зі швидкістю 60 км/год, а потім 3 год йшли пішки зі швидкістю 4 км/год. Чому дорівнює весь шлях, подоланий туристами?
Розв'язання.
60 • 2 = 120 (км) – шлях поїздом.
4 • 3 = 12 (км) – шлях пішки.
120 + 12 = 132 (км) – увесь шлях.
Відповідь: 132 кілометри.
Зміни запитання у задачі так, щоб останньою дією в розв'язанні було віднімання.
На скільки відстань поїздом більша, ніж пішки?
120 – 12 = 108 (км) – на стільки відстань поїздом більша, ніж пішки.
Відповідь: на 108 кілометрів.
Завдання 3. Відстань між двома містами 75 км. Третину цієї відстані поїзд подолав за 25 хв. З якою швидкістю рухався поїзд? Розв'яжи задачу складанням виразу.
Розв'язання.
75 : 3 : 25 = 1 (км/хв) – швидкість поїзда.
75 : 3 = 25 (км) – третина шляху.
25 : 25 = 1 (км/хв) – швидкість поїзда.
Відповідь: 1 км/хв.
Завдання 4. 90 т вугілля одна вантажівка може перевезти за 15 рейсів, а друга — за 10 рейсів. За скільки рейсів перевезуть це вугілля вантажівки, якщо працюватимуть разом?
Розв'язання.
90 : 15 = 6 (т) – перевозить тонн перша вантажівка за 1 рейс.
90 : 10 = 9 (т) – перевозить тонн друга вантажівка за 1 рейс.
6 + 9 = 15 (т) – перевозять тонн разом вантажівки за один рейс.
90 : 15 = 6 (р.) – за стільки рейсів перевезуть разом увесь вантаж.
Відповідь: 6 рейсів.
Завдання 5*. У класі 7 дітей відвідують спортзал щодня, 9 — відвідують через день, а решта — взагалі не відвідують. Учора в спортзалі займалось 13 дітей цього класу. Скільки дітей прийдуть у спортзал сьогодні?
Розв'язання.
Займаються 7 + 9 = 16 дітей або 7 дітей. Якщо вчора в спортзалі займалось 13 дітей цього класу, то сьогодні прийде не більше, ніж 7 дітей.
Відповідь: до 7 дітей.
До № 550-566
Завдання 1.
|
х 3275 4 13100 |
х 24036 7 168252 |
х 328204 3 984612 |
х 6500 4 26000 |
х 20030 6 120180 |
х 58004 8 464032 |
Завдання 2. За даними таблиці склади й розв'яжи задачу.
|
Швидкість |
Час |
Відстань |
|
56 км/год ? |
3 год 2 год |
однакова |
Перший автомобіль їхав зі швидкістю 56км/год і прибув до місця призначення за 3 год, другий подолав цей шлях за дві години. З якою швидкістю їхав другий автомобіль?
Розв'язання.
56 • 3 = 168 (км) – довжина дороги.
168 : 2 = 84 (км/год) – швидкість другого автомобіля.
Відповідь: 84 км/год.
Завдання 3. У майстерню привезли а м тканини. За тиждень із четвертої частини тканини пошили сукні, витративши на кожну по 3 м. Скільки пошили суконь? Склади вираз, за допомогою якого розв'язується задача.
Розв'язання.
Вираз а : 4 : 3 (с.) – пошили суконь.
а : 4 (м) – четверта частина тканини.
а : 4 : 3 (с.) – пошили суконь.
Відповідь: а : 4 : 3 суконь.
Завдання 4. Добери й запиши всі одноцифрові числа, які є розв'язками нерівностей.
180 : х < 40 а • 20 > 125 Ь : 2 < 5
х = 5,6,7,8,9 а = 7,8,9 Ь = 9,8,7,6,5,4,3,2,1,0
Завдання 5*. На стадіон прийшло 7 хлопчиків і 6 дівчаток. Пізніше до них підійшло ще декілька дітей. Усі діти розділилися на 2 команди з однаковою кількістю учасників. У кожній команді кількість дівчаток і кількість хлопчиків однакова. Яка найменша кількість дітей, що підійшли на стадіон пізніше?
Розв'язання.
(7 + 1) : 2 = 4 (д.) - хлопчиків у команді.
(6 + 2) : 2 = 4 (д.) – дівчаток у команді.
Підійшли 1 хлопчик та 2 дівчинки, разом 3 дітей.
Відповідь: 3 дитини.
До № 567-582
Завдання 1. Обчисли ланцюжки. Відповіді запиши.
|
4800 : 10 : 3 • 8 + 140 1420 |
640 : 20 • 100 + 400 : 10 360 |
1000 – 360 : 10 : 8 • 0 0 |
2360 – 2060 : 2 • 10 + 150 1650 |
4800 : 10 = 480
480 : 3 = (300 + 180) : 3 = 100 + 60 = 160
160 • 8 = (100 + 60) • 8 = 800 + 480 = 1280
1280 + 140 = 1420
640 : 20 = (600 + 40) : 20 = 30 + 2 = 32
32 • 100 = 3200
3200 + 400 = 3600
3600 : 10 = 360
а • 0 = 0
2360 – 2060 = 300
300 : 2 = 150
150 • 10 = 1500
1500 + 150 = 1650
Завдання 2. Виконай дії письмово. Запиши значення виразів.
1) 3 • 2308 + 4080 • 6 = 31404
|
х 2308 3 6924 |
х 4080 6 24480 |
+ 24480 6924 31404 |
6709 + 7 • 6500 = 52209
|
х 6500 7 45500 |
+ 45500 6709 52209 |
2) 4 км 260 м • 4 = 17 км 40 м
З т 045 кг • 6 = 18 т 270 кг
|
х 4 км 260 м 4 17 км 040 м |
х 3 т 045 кг 6 18 т 270 кг |
Завдання 3. Периметр трикутника, у якого всі сторони рівні, 7 см 5 мм. Побудуй квадрат, довжина сторони якого дорівнює довжині сторони трикутника. Знайди його периметр.
Розв'язання.
Нагадаємо, що 7см 5мм = 75 мм, тому
75 : 3 = 25 (мм) = 2 см 5 мм – довжина сторони трикутника.
25 • 4 = 100 (мм) = 10 (см) – периметр квадрата.
Відповідь: 10 сантиметрів.
Завдання 4. Одна бригада може виготовити 360 деталей за 12 днів, а друга — за 6 днів. За скільки днів буде виготовлено 360 деталей, якщо бригади працюватимуть разом?
Розв'язання.
360 : 12 = 30 (д.) – деталей виготовляє перша бригада за 1 день.
360 : 6 = 60 (д.) – деталей виготовляє друга бригада за 1 день.
30 + 60 = 90 (д.) – деталей виготовлять дві бригади за 1 день.
360 : 90 = 4 (д.) – за стільки днів будуть виготовлені деталі, якщо бригади працюватимуть разом.
Відповідь: за 4 дні.
Завдання 5*. Сума двох чисел 876, а їх різниця — 224. Знайди ці числа.
Розв'язання.
Число1 + число2 + (число1 – число2) = 876 + 224, тоді
2 • число1 = 1100 – подвоєне перше число.
1100 : 2 = 550 – перше число.
876 – 550 = 326 – друге число.
Відповідь: 550, 326.
До № 583-601
Завдання 1. Обчисли ланцюжки. Відповіді запиши.
|
70 • 90 : 100 • 5 + 85 400 |
400 : 8 • 9 : 3 • 6 900 |
900 : 300 • 7 – 4 • 5 85 |
850 – 800 : 50 • 200 : 5 40 |
70 • 90 = 6300
6300 : 100 = 63
63 • 5 = (60 + 3) • 5 = 300 + 15 = 315
315 + 85 = 400
400 : 8 = 50
50 • 9 = 450
450 : 3 = (300 + 150) : 3 = 100 + 50 = 150
150 • 6 = (100 + 50) • 6 = 600 + 300 = 900
900 : 300 = 3
3 • 7 = 21
21 – 4 = 17
17 • 5 = (10 + 7) • 5 = 50 + 35 = 85
850 – 800 = 50
50 : 50 = 1
1 • 200 = 200
200 : 5 = 40
Завдання 2. Обчисли письмово.
|
х 80607 4 322428 |
х 9009 9 81081 |
х 5700 8 45600 |
х 30025 7 21175 |
х 43050 6 258300 |
х 63008 5 315040 |
Завдання 3. На двох складах було 6080 кг зерна. Коли з першого складу видали 820 кг, а з другого — в 4 рази більше, то на другому складі нічого не залишилося. Скільки кілограмів зерна залишилося на першому складі?
Розв'язання.
1 спосіб.
820 • 4 = 3280 (кг) – було зерна на другому складі.
3280 + 820 = 4100 (кг) - видали зерна з двох складів.
6080 - 4100 = 1980 (кг) - зерна залишилося на першому складі.
2 спосіб.
820 • 4 = 3280 (кг) – було зерна на другому складі.
6080 – 3280 = 2800 (кг) – було зерна на першому складі.
2800 – 820 = 1980 (кг) – зерна залишилося на першому складі.
Відповідь: 1980 кілограмів.
Завдання 4. Заповни таблицю.
|
Довжина (см) |
80 |
18 |
630 : 7 = 90 |
300 : 3 = 100 |
720 : 9 = 80 |
|
Ширина (см) |
9 |
8 |
7 |
3 |
9 |
|
Площа (см2) |
80 • 9 = 720 |
18 • 8 = 144 |
630 |
300 |
720 |
Завдання 5*. Прямокутник розділили на 3 квадрати однакової площі. Знайди площу й периметр квадрата, якщо довжина прямокутника 90 см.
Розв'язання.
90 : 3 = 30 (см) – довжина сторони квадрата.
30 • 30 = 900 (см2) – площа квадрата.
30 • 4 = 120 (см) – периметр квадрата.
Відповідь: 900 см2, 120 см.
До № 602-616
Завдання 1. Швидкість польоту орла 30 м/с, а сокола — 23 м/с. На скільки метрів більше може пролетіти за 10 с орел, ніж сокіл? Розв'яжи задачу двома способами, склавши вирази.
Розв'язання.
1 спосіб.
30 • 10 – 23 • 10 = 70 (м) – на стільки більше метрів може пролетіти орел, ніж сокіл.
30 • 10 = 300 (м) – шлях пролітає орел.
23 • 10 = 230 (м) – шлях пролітає сокіл.
300 – 230 = 70 (м) – на стільки більше метрів може пролетіти орел, ніж сокіл.
2 спосіб.
(30 – 23) • 10 = 70 (м) - на стільки більше метрів може пролетіти орел, ніж сокіл.
30 – 23 = 7 (м) – на стільки більше метрів пролітає за 1 секунду орел, ніж сокіл.
7 • 10 = 70 (м) – на стільки більше метрів може пролетіти орел, ніж сокіл.
Відповідь: на 70 метрів.
Завдання 2. Порівняй вирази усно. Перевір, виконавши дії.
1) 486 • 9 > 435 • 9 8 • 1046 < 4092 • 4
1046 • 8 = 1046 • 2 • 4 = (1000 + 40 + 6) • 2 • 4 = (2000 + 80 + 12) • 4 = 2092 • 4
2) 357 • 6 < 457 • 5 7200 • 3 = 6 • 3600
300 • 6 < 400 • 5
6 • 3600 = 3 • 2 • 3600 = 3 • 2 • (3000 + 600) = 3 • (6000 + 1200) = 3 • 7200
Завдання 3. Знайди на малюнку 5 чотирикутників. Запиши їх. Які з них прямокутники? Запиши. Знайди периметр і площу кожного прямокутника.
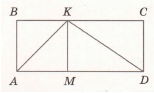
Чотирикутники: ABCD; ABKM; MKCD; ABKD; AKCD.
Прямокутники: ABCD; ABKM; MKCD,
Завдання 4. Птахофабрика повинна відправити до магазинів 6000 яєць. Було відправлено 10 ящиків по 350 яєць і 4 ящики по 250 яєць. Скільки яєць залишилося відправити до магазинів?
Розв'язання.
350 • 10 + 250 • 4 = 4500 (ящ.) – ящиків відправлено.
6000 – 4500 = 1500 (ящ.) – ящиків залишилось відправити.
Відповідь: 1500 ящиків.
Завдання 5. На пошиття 6 пар черевиків потрібно 24 дм2 шкіри. Скільки квадратних дециметрів шкіри потрібно для пошиття 16 пар черевиків?
Розв'язання.
24 : 6 = 4 (дм2) – потрібно шкіри для пошиття 1 пари черевиків.
4 • 16 = 64 (дм2) – потрібно шкіри для пошиття 16 пар черевиків.
Відповідь: 64 дм2.
До № 617-633
Завдання 1. Виконай дії письмово. Відповіді запиши.
1576 • 8 + 3040 • 7 = 33888
|
х 1576 8 12608 |
х 3040 7 21280 |
+ 12608 21280 33888 |
5700 • 6 + 4095 • 3 = 40785
|
х 5700 5 28500 |
х 4095 3 12285 |
+ 28500 12285 40785 |
Завдання 2. За планами ділянок знайди, яку площу відведено окремо для вирощування капусти, буряків і цибулі.
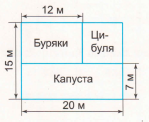
Для капусти: 20 • 7 = 140 (м2)
Для буряків: 12 • (15 – 7) = 12 • 8 = 96 (м2)
Для цибулі: (15 – 7) • (20 – 12) = 8 • 8 = 64 (м2)
Завдання 3. Знайди значення виразу а • Ь, якщо:
1) а = 5, Ь = 4080; 2) а = 4, b = 4320; 3) а = 7068, b = 8.
1) Якщо а = 5, Ь = 4080, тоді а • Ь = 5 • 4080 = 20400
|
х 4080 5 20400 |
2) Якщо а = 4, Ь = 4320, тоді а • Ь = 4 • 4320 = 17280
|
х 4320 4 17280 |
3) Якщо а = 8, Ь = 7068, тоді а • Ь = 8 • 7068 = 56544
|
х 7068 8 56544 |
Завдання 4. Площа ділянки прямокутної форми 8 а. Довжина однієї зі сторін дорівнює 20 м. Знайди довжину другої сторони ділянки.
Розв'язання.
Нагадаємо, що 1 а = 100 м2.
800 : 20 = 40 (м) – довжина другої сторони ділянки.
Відповідь: 40 метрів.
Завдання 5*. Довжина огорожі навколо ділянки (периметр) прямокутної форми 680 м. Ширина ділянки на 40 м менша від довжини. Знайди довжину сторін цієї ділянки.
Розв'язання.
1 спосіб.
Оскільки периметр обчислюється за формулою P = 2 • (a + b), де а - довжина, b - ширина, тоді сума довжини і ширини рівна половині периметра,
тобто а + b = Р:2
За умовою задачі довжина b=a+40, тому а+а+40=P:2
680 : 2 = 340 (м) – сума довжини та ширини ділянки.
340 – 40 = 300 (м) – подвійна ширина ділянки.
300 : 2 = 150 (м) – ширина ділянки.
150 + 40 = 190 (м) – довжина ділянки.
2 спосіб.
Нехай х (м) – ширина ділянки , тоді х + 40 (м) – довжина ділянки, складемо рівняння:
Периметр обчислюється за формулою P = 2 • (a + b), де а - довжина, b - ширина.
2 • ( х + х + 40)= 680
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
(х + х + 40) = 680 : 2
2х + 40 = 340
Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.
2х = 340 – 40
2х = 300
х = 300 : 2
х = 150
150 (м) – ширина ділянки, тоді
150 + 40 = 190 (м) – довжина ділянки.
Відповідь: 190 метрів.