До № 634-654
Завдання 1. Заповни таблицю.
|
а |
96 |
16 • 8 = 128 |
48 |
600 |
18 • 7 = 126 |
64 |
0 |
|
b |
6 |
8 |
48 : 12 = 4 |
2 |
18 |
64 : 4 = 16 |
9 |
|
а : b |
96 : 6 = 16 |
16 |
12 |
600 : 2 = 300 |
7 |
4 |
0 : 9 = 0 |
Завдання 2. Які остачі можуть бути при діленні на 6?
Остачі не можуть бути більшими від дільника.
При діленні на 6 остачі можуть бути від 1 до 5.
Завдання 3. Виконай ділення з остачею.
10 дес. : 3 = 33 (ост. 1) 42 : 5 = 8 (ост. 2)
1 сот. : 3 = 33 ( ост. 1) 20 : 6 = 3 (ост. 2)
100 : 3 = 33 (ост. 1), бо 33 • 3 + 1 = 100 = 10 дес.
100 : 3 = 33 (ост. 1) , бо 33 • 3 + 1 = 100 = 1 сот.
42 : 5 = 8 (ост. 2), бо 8 • 5 + 2 = 42
20 : 6 = 3 (ост. 2), бо 3 • 6 + 2 = 20
Завдання 4. Заповни пропуски.
8 дм2 = 800 см2
1900 см2 = 19 дм2
15 а = 1500 м2
42 000 м2 = 420 а
Нагадаємо, що 1 дм = 10 см, 1 дм2 = 100 см2, 1 а = 100 м2
1 спосіб.
8 дм2 = 8 • 100 см2 = 800 см2
1900 см2 = (1900 : 100) дм2 = 19 дм2
15 а = 15 • 100 м2 = 1500 м2
42000 м2 = (42000 : 100) а = 420 а
2 спосіб.
8 дм2 = 8 • дм • дм = 8 • 10 см • 10 см = 800 см2
1900 см2 = 1900 • см • см = 19 • 10 см • 10 см = 19 • дм • дм = 19 дм2
15 а = 15 • 100 м2 = 1500 м2
42000 м2 = 420 • 10 м • 10 м = 420 • 100 м2 = 420 а
Завдання 5. Виконай ділення письмово. Запиши значення виразів. Перевір множенням.
2296 : 8 = 287
2086 : 7 = 298
3714 : 6 = 619
|
2296| 8 16 │287 69 64 56 56 0 |
2086| 7 14 │298 68 63 56 56 0 |
3714| 6 36 │619 11 6 54 54 0 |
Завдання 6. У швейній майстерні з 280 м тканини пошили сукні та зі 150 м тканини — сорочки. На кожну сукню витрачали 4 м тканини, а на сорочку — 3 м. Чого більше пошили і на скільки?
Розв'язання.
280 : 4 = 70 (шт.) – пошили суконь.
150 : 3 = 50 (шт.) – пошили сорочок.
70 – 50 = 20 (шт.) – на стільки більше пошили суконь, ніж сорочок.
Відповідь: на 20 штук.
До № 655-671
Завдання 1. Три муляри за 4 год уклали 3360 цеглин, порівну кожний. Скільки цеглин уклав один муляр за З год?
Розв'язання.
1 спосіб
3360 : 4 = 840 (ц) – цеглин уклали три мулярі за годину.
840 : 3 = 280 (ц) – цеглин уклав один муляр за годину.
280 • 3 = 840 (ц) – цеглин уклав один муляр за 3 години.
2 спосіб
3360 : 3 = 1120 (ц) – цеглин уклав один муляр за 4 години.
1120 : 4 = 280 (ц) – цеглин уклав один муляр за годину.
280 • 3 = 840 (ц) – цеглин уклав один муляр за 3 години.
3 спосіб.
3 • 4 = 12 (год) – годин працювали мулярі.
3360 : 12 = 280 (ц) – цеглин уклав один муляр за годину.
280 • 3 = 840 (ц) – цеглин уклав один муляр за 3 години.
Відповідь: 840 цеглин.
Завдання 2. Площа вікон у класі повинна становити 1/5 площі підлоги. Яка буде площа вікон класу, якщо його довжина 10 м, а ширина — 6 м?
Розв'язання.
10 • 6 = 60 (м2) – площа підлоги.
60 : 5 • 1 = 12 (м2) – площа вікон у класі.
Відповідь: 12 м2.
Завдання 3. Заповни пропуски.
1/5 м2 = 20 дм2
1/10 га = 1000 м2
1/4 а = 25 м2
Нагадаємо, що 1 м2 = 100 дм2, 1 а = 100 м2, 1 га = 100 а = 10 000 м2
1/5 м2 = 100 дм2 : 5 • 1 = 20 дм2
1/10 га = 10 000 м2 : 10 • 1 = 1000 м2
1/4 а = 100 м2 : 4 • 1 = 25 м2
Завдання 4. Виконай дії з іменованими числами.
1) 5 кг 200 г – 2 кг 500 г = 2 кг 700 г
21 м З0 см + 6 м 75 см = 28 м 5 см
|
-5кг200г 2кг500г 2кг700г |
+21м30см 6м75см 28м05см |
2) 23 м 40 см : 3 = 7 м 80 см
35 ц 80 кг : 4 = 8 ц 95 кг
|
2340| 3 21 │780 24 24 0 |
3580| 4 32 │895 38 36 20 20 0 |
Завдання 5*. Знайди різницю двох п'ятицифрових чисел, сума цифр яких дорівнює 8.
- 20006
10007
9999
До № 672-687
Завдання 1. Висота найвищої вершини Карпат Говерли 2061 м. Це на 516 м вище від вершини Роман-Кош, що в Криму. Яка заввишки Роман-Кош?
Розв'язання.
2061 – 516 = 1545 (м) – висота Роман-Кош.
Відповідь: 1545 метрів.
Завдання 2. Виконай ділення з остачею.
35 : 8 = 4 (ост. 3) , бо 4 • 8 + 3 = 35
9 : 5 = 1 (ост. 4) , бо 1 • 5 + 4 = 9
402 : 100 = 4 (ост. 2), бо 4 • 100 + 2 = 402
4 : 3 = 1 (ост. 1), бо 1 • 3 + 1 = 4
Завдання 3.
|
- 35147| 7 35 │5021 1 0 14 14 7 7 0 |
-28032| 4 28 │7008 3 0 32 32 0 |
Завдання 4. Площа прямокутника 1600 м2, а довжина сторони 80 м. Знайди площу квадрата, периметр якого дорівнює периметру прямокутника.
Розв'язання.
1600 : 80 = 20 (м) – ширина прямокутника.
(80 + 20) • 2 = 200 (м) – периметр прямокутника.
200 : 4 = 50 (м) – сторона квадрата.
50 • 50 = 2500 (м2) – площа квадрата.
Відповідь: 2500 м2.
Завдання 5*. Турист мав пройти 36 км. Після привалу йому залишилося пройти ще третину того, що пройшов до привалу. На скільки кілометрів менше залишилося пройти туристу, ніж він уже пройшов?
Розв'язання.
1 спосіб.
До привалу турист пройшов 3 частини шляху, після привалу одну 1 частину шляху, тому увесь шлях складається із 4 частин.
36 : 4 • 3 = 27 (км) – пройшов турист до привалу.
36 : 4 • 1 = 9 (км) – пройшов турист після привалу.
27 – 9 = 18 (км) - на стільки кілометрів менше залишилося пройти туристу, ніж він уже пройшов.
2 спосіб.
До привалу турист пройшов 3 частини шляху, після привалу одну 1 частину шляху, тому увесь шлях складається з 4 частин.
3 – 1 = 2 (частини) – на стільки частин шлях після привалу менший.
36 : 4 • 2 = 18 (км) – на стільки кілометрів шлях після привалу менший.
Відповідь: на 18 кілометрів.
До № 688-705
Завдання 1. Обчисли ланцюжки. Відповіді запиши.
60 • 40 180 : 3 1400 : 7 50 000 : 5
: 24 • 70 • 20 : 2
• 90 : б : 5 • 8
: 5 • 0 • 6 : 100
1800 0 4800 400
60 • 40 = 2400
2400 : 24 = 100
100 • 90 = 9000
9000 : 5 = (5000 + 4000) : 5 = 1000 + 800 = 1800
а • 0 = 0
1400 : 7 = 200
200 • 20 = 4000
4000 : 5 = 800
800 • 6 = 4800
50 000 : 5 = 10 000
10 000 : 2 = 5 000
5 000 • 8 = 40 000
40 000 : 100 = 400
Завдання 2. Обчисли письмово. Запиши значення виразів.
21 012 : 3 = 7004
42 630 : 7 = 6090
63 ц 36 кг : 9 = 7 ц 4 кг
|
- 21012| 3 21 │7004 1 0 12 12 0 |
-42630| 7 42 │6090 6 0 63 63 0 |
- 6336| 9 63 │704 3 0 36 36 0 |
Завдання 3. За 2 год бульдозер розчищає 12 га землі, а робітник за 6 год — 180 м2. Скількох робітників замінює один бульдозер? Розв'язуючи задачу, міркуй за схемою.
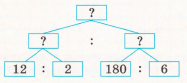
Розв'язання.
Нагадаємо, що 1 га = 1000 м2
12000 : 2 = 6000 (м2) – розчищає бульдозер за 1 год.
180 : 6 = 30 (м2) – розчищає робітник за 1 год.
6000 : 30 = 200 (р.) – робітників заміняє один бульдозер.
Відповідь: 200 робітників.
Завдання 4. 24 серпня 1991 року в день проголошення незалежності України народився хлопчик Ярослав. Визнач вік Ярослава на сьогодні.
Розв'язання.
2016 – 1991 = 25 (р.) – років Ярославу.
Відповідь: 25 роки.
Завдання 5*. Сума чисел, що позначають номери трьох будинків, які стоять поряд на одному боці вулиці, дорівнює 147. Визнач номери цих будинків.
Розв'язання.
147 : 3 = 49 (н.) – номер середнього будинку.
Оскільки на вулиці номери непарні, маємо 47, 49, 51.
Відповідь: 47, 49, 51.
До № 706-722
Завдання 1.
42 000 : 7 = 6 000
36 т 42 кг : 6 = 6 т 7 кг
2 т 40 кг : 8 = 240 кг : 8 = 30 кг
16 000 : 4 = 4 000
48 км 180 м : 3 = 16 км 60 м
3 км 500 м : 7 = 3500 м : 7 = 500 м
Завдання 2. З двох міст одночасно назустріч один одному виїхали автобус і легковий автомобіль. Швидкість автобуса 60 км/год, а легкового автомобіля — 80 км/год. Через 3 год вони зустрілися. Яка відстань між містами? Розв'яжи задачу двома способами, склавши вирази.
Розв'язання.
1 спосіб.
60 • 3 + 80 • 3 = 420 (км) – відстань між містами.
60 • 3 = 180 (м) – відстань проїхав автобус.
80 • 3 = 240 (км) – відстань проїхав автомобіль.
180 + 240 = 420 (км) – відстань між містами.
2 спосіб.
(60 + 80) • 3 = 420 (км) – відстань між містами.
60 + 80 = 140 (км) – проїдуть автобус та автомобіль за 1 год.
140 • 3 = 420 (км) - проїдуть автобус та автомобіль за 3 год, тобто відстань між містами.
Відповідь: 240 кілометрів.
Завдання 3. Запиши тільки корені рівнянь.
9 • х = 72 045 240 000 : х = 8
х = 8005 х = 30 000
9 • х = 72 045
Щоб знайти невідомий множник, треба добуток поділити на відомий множник
х = 72 045 : 9
х = 8005
|
-72045| 9 72 │8005 4 0 45 45 0 |
240 000 : х = 8
Щоб знайти невідомий дільник, треба ділене поділити на частку
х = 240 000 : 8
х = 30 000
Завдання 4. На 1 м2 картопляного поля вносять 3 кг перегною. Скільки кілограмів перегною потрібно внести на ділянку прямокутної форми, довжина якої 70 м, а ширина — 8 м?
Розв'язання.
70 • 8 = 560 (м2) – площа прямокутної ділянки.
560 • 3 = 1680 (кг) – кілограмів перегною треба внести.
Відповідь: 1680 кілограмів.
Завдання 5. Висота надводної частини айсберга 12 м. Це 1/6 частина висоти всього айсберга. На скільки метрів підводна частина айсберга більша від висоти його надводної частини?
Розв'язання.
1 спосіб.
Якщо 12 м уже становить 1/6 айсберга, тоді
12 : 1 • 6 = 72 (м) – висота айсберга.
72 – 12 = 60 (м) – висота підводної частини айсберга.
60 – 12 = 48 (м) – на стільки метрів підводна частина айсберга більша від висоти його надводної частини.
2 спосіб.
Оскільки увесь айсберг має 6 частин, тому
5/6 – 1/6 = 4/6 (ч) – на стільки частин підводна частина айсберга більша від висоти його надводної частини.
12 • 6 = 72 (м) – висота айсберга.
72 : 6 • 4 = 48 (м) - на стільки метрів підводна частина айсберга більша від висоти його надводної частини.
Відповідь: на 48 метрів.
Завдання 6*. Периметр прямокутника дорівнює 24 см. Його довжина у 2 рази більша, ніж ширина. Побудуй цей прямокутник і знайди його площу.
Розв'язання.
24 : 2 = 12 (см) – сума довжини та ширини прямокутника.
На довжину припадає 2 частини, на ширину – 1 частина, разом 3 частини, тоді
12 : 3 = 4 (см) – припадає на 1 частину або ширина прямокутника.
4 • 2 = 8 (см) – довжина прямокутника.
4 • 8 = 32 (см2) - площа прямокутника.
Відповідь: 32 см2.
До № 723-750
Завдання 1. Обчисли ланцюжки.
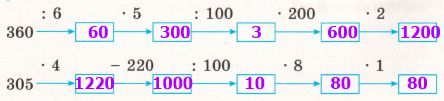
360 : 6 = 60
60 • 5 = 300
300 : 100 = 3
3 • 200 = 600
600 • 2 = 1200
305 • 4 = (300 + 5) • 4 = 1200 + 20 = 1220
1220 – 220 = 1000
1000 : 100 = 10
10 • 8 = 80
80 • 1 = 80
Завдання 2. З двох міст, відстань між якими 42 км, виїхали одночасно назустріч один одному два вершники і зустрілися через 2 год. Перший вершник їхав зі швидкістю 12 км/год. З якою швидкістю їхав другий вершник? Розв'яжи задачу двома способами, склавши вирази.
Розв'язання.
(42 – 12 • 2 ) : 2 = 9 (км/год) – швидкість другого вершника.
12 • 2 = 24 (км) – проїхав перший вершник.
42 – 24 = 18 (км) – проїхав другий вершник.
18 : 2 = 9 (км/год) – швидкість другого вершника.
Відповідь: 9 км/год.
Завдання 3. Катер пройшов за течією річки 180 км за 6 год і повернувся назад. Скільки годин ішов катер проти течії річки, швидкість якої 5 км/год?
Розв'язання.
180 : 6 = 30 (км/год) – швидкість катера за течією річки (власна швидкість катера плюс швидкість течії річки).
30 – 5 = 25 (км/год) – власна швидкість катера.
25 – 5 = 20 (км/год) – швидкість катера проти течії річки (власна швидкість катера мінус швидкість течії річки).
180 : 20 = 9 (год) – годин ішов катер проти течії річки.
Відповідь: 9 годин.
Завдання 4. У їдальні за три місяці використали 1224 кг овочів. За перший місяць використали третю частину всіх овочів, за другий — у 2 рази менше, ніж за перший. Скільки кілограмів овочів використали в їдальні за третій місяць?
Розв'язання.
1224 : 3 = 408 (кг) – кілограмів овочів використали за перший місяць.
408 : 2 = 204 (кг) – кілограмів овочів використали за другий місяць.
408 + 204 = 612 (кг) – кілограмів овочів використали за перший та другий місяць разом.
1224 – 612 = 612 (кг) - кілограмів овочів використали за третій місяць.
2 спосіб.
1/3 = 2/6
6 – усього частин.
2 (частини) – припадає на перший місяць.
2 : 2 = 1 (частина) – припадає на другий місяць.
6 – 1 – 2 = 3 (частини) – припадає на третій місяць.
1224 : 6 • 3 = 612 (кг) - кілограмів овочів використали за третій місяць.
Відповідь 612 кілограмів.
Яку додаткову дію треба буде виконати в задачі, якщо змінити запитання так: на скільки кілограмів овочів витратили більше за третій місяць, ніж за перший?
612 – 408 = 204 (кг) – на стільки кілограмів овочів витратили більше за третій місяць, ніж за перший.
Завдання 5.
8 кг – 3 кг 75 г > 7 кг – 2 кг 250 г
5 т – 2 т 250 кг > 6 т – 3 т 750 кг
6 км – 760 м > 3 км 560 м + 1 км 630 м
З доби – 18 год < 5 діб 6 год + 2 доби 12 год
8 кг – 3 кг 75 г = 8 кг – 3 кг – 75 г = 5 кг – 75 г = 4 кг + 1 кг – 75 г = 4кг + 1000г – 75г = 4 кг + 925г = 4кг 925 г
7 кг – 2 кг 250 г = 7 кг – 2 кг – 250 г = 5 кг – 250г = 4 кг + 1кг – 250 г = 4 кг + 1000 г – 250 г = 4 кг 750 г
5 т – 2 т 250 кг = 5т – 2т – 250 кг = 3 т – 250 кг = 2т + 1т - 250 кг = 2т + 1000кг – 250 кг = 2т + 750 кг = 2т 750 кг
6 т – 3 т 750 кг = 6т – 3 т – 750 кг = 3 т – 750 кг = 2 т + 1 т – 750 кг = 2т + 1000 кг – 750 кг = 2 т 250 кг
6 км – 760 м = 5 км + 1 км – 760 м = 5 км + (1000 м – 760 м) = 5 км 240 м
3 км 560 м + 1 км 630 м = 4 км + 560 м + 630 м = 4 км + 1190 м = 5 км 190 м
З доби – 18 год = 2 доби + 1 доба – 18 год = 2 доби + 24 год – 18 год = 2 доби 6 год
5 діб 6 год + 2 доби 12 год = 7 діб 18 год
2 доби < 7 діб
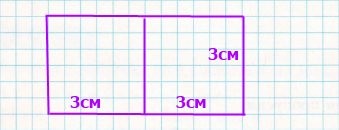
Завдання 6*. Побудуй прямокутник площею 18 см2, який можна розділити на 2 рівних квадрати.
Розв'язання.
(3 • 2) • 3 = 18 (см2) – площа прямокутника з довжиною 6см та шириною 3см.