До №1013-1027
Завдання 1. Фермер підготував до відправки на консервний завод 3200 кг помідорів, 2/5 цих помідорів розклав у ящики, по 20 кг у кожний, а решту — в інші ящики, по З0 кг у кожний. Скільки всього ящиків знадобилося?
Розв'язання.
3200 : 5 • 2 = 1280 (кг) – помідори у ящиках по 20 кг.
1280 : 20 = 64 (ящ.) – яшиків по 20 кг.
3200 – 1280 = 1920 (кг) – решта помідорів.
1920 : 30 = 64 (ящ.) – ящиків по 30 кг.
64 + 64 = 128 (ящ.) – знадобилося ящиків.
Відповідь: 128 ящиків.
Завдання 2. Виконай ділення письмово. Запиши значення виразів. Перевір множенням.
77 880 : 55 = 1416 29 736 : 56 = 531
|
-77880| 55 55 1416 228 220 88 55 330 330 0 |
х 1416 55 + 7080 7080 77880 |
-29736| 56 280 531 173 168 56 56 0 |
х 531 56 +3186 2655 29736 |
Завдання 3. Довжина прямокутника а м, а ширина — на 20 м менша. Знайди периметр і площу прямокутника.
Розв'язання.
а – 20 (м) – ширина прямокутника.
а • (а – 20) (м2) – площа прямокутника.
2 • (а + (а – 20)) = 2 • (2а - 20) (м) – периметр прямокутника.
Завдання 4*. Кінь перші 3 год біг зі швидкістю 15 км/год, а потім 2 год — зі швидкістю на 5 км/год меншою. Знайди середню швидкість бігу коня.
Розв'язання.
15 • 3 = 45 (км) – перша відстань.
15 – 5 = 10 (км/год) – друга швидкість.
10 • 2 = 20 (км) – друга відстань.
20 + 45 = 65 (км) – уся відстань.
3 + 2 = 5 (год) – весь час.
65 : 5 = 13 (км/год) – середня швидкість бігу.
Відповідь: 13 км/год.
Завдання 5*. Віднови пропущені цифри.
|
-9 * * *| 3 * * 6 * * * 2* 4 * ** 0 |
-6 * 8| * 4 * * 7 1 6 * * * * 0 |
-* * * *| * 5 * 7 * 2 * 5 9 * * * * 0 |
|
-9 8 2 4| 3 2 9 6 3 0 7 2 2 4 2 2 4 0 |
-6 4 8| 2 4 4 8 2 7 1 6 8 1 6 8 0 |
-2 2 9 5| 8 5 1 7 0 2 7 5 9 5 5 9 5 0 |
До № 1028-1050
Завдання 1. Обчисли ланцюжки.
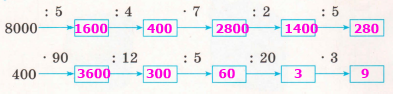
8000 : 5 = (5000 + 3000) : 5 = 1000 + 600 = 1600
1600 : 4 = 400
400 • 7 = 2800
2800 : 2 = 1400
1400 : 5 = (1000 + 400) : 5 = 200 + 80 = 280
400 • 90 = 3600
3600 : 12 = 3600 : (6 • 2) = 3600 : 6 : 2 = 600 : 2 = 300
300 : 5 = 60
60 : 20 = 3
3 • З = 9
Завдання 2. Двома жатками скосили овес із площі 96 га за 8 год. За скільки годин однією такою жаткою скосили овес із площі З0 га?
Розв'язання.
1 спосіб.
96 : 2 = 48 (га) – косять однією жаткою за 8 годин.
48 : 8 = 6 (га) – косять однією жаткою за 1 год.
30 : 6 = 5 (год) – за стільки годин однією такою жаткою скосили овес із площі З0 га.
2 спосіб.
96 : 8 = 12 (га) – косять двома жатками за 1 годину.
12 : 2 = 6 (га) – косять однією жаткою за 1 год.
30 : 6 = 5 (год) – за стільки годин однією такою жаткою скосили овес із площі З0 га.
Відповідь: 5 годин.
Завдання З*. На двох ділянках, площею 6 га і 10 га, посіяли 1920 кг насіння льону. Скільки кілограмів насіння льону було посіяно на кожній ділянці, якщо норми висіву однакові?
Розв'язання.
1 спосіб.
6 + 10 = 16 (га) – площа двох ділянок.
1920 : 16 = 120 (кг) – посіяно льону на 1га.
120 • 10 = 1200 (кг) – посіяно льону на другій ділянці.
1920 – 1200 = 720 (кг) – посіяно льону на першій ділянці.
2 спосіб.
6 + 10 = 16 (га) – площа двох ділянок.
1920 : 16 = 120 (кг) – посіяно льону на 1га.
120 • 10 = 1200 (кг) – посіяно льону на другій ділянці.
120 • 6 = 720 (кг) – посіяно льону на першій ділянці.
3 спосіб.
Умовно можна вважати, що поле складається із
6 + 10 = 16 (ч.) – частини, що складають усе поле.
1920 : 16 • 6 = 720 (кг) – посіяно льону на першій ділянці.
1920 : 16 • 10 = 1200 (кг) – посіяно льону на другій ділянці.
Відповідь: 720 кілограмів, 1200 кілограмів.
Завдання 4. У кімнаті, довжина якої 6 м, а ширина на 2 м менша, треба викласти плитками підлогу. Скільки потрібно плиток, площа яких 4 дм2.
Розв'язання.
Нагадаємо, що 1 м = 10 дм.
60 – 20 = 40 (дм) – ширина підлоги.
60 • 40 = 2400 (дм2) – площа підлоги.
2400 : 4 = 600 (пл.) – потрібно плиток.
Відповідь: 600 плиток.
Завдання 6. Автомобіль першого дня проїхав 480 км, а другого — 2/3 того, що проїхав першого дня. На кожні 100 км шляху він витрачав 9 л бензину. Скільки всього літрів бензину витратив автомобіль за два дні?
Розв'язання.
480 : 3 • 2 = 320 (км) – проїхав автомобіль другого дня.
480 + 320 = 800 (км) – проїхав автомобіль за два дні.
800 : 100 • 9 = 72 (л) – літрів бензину витратив автомобіль.
Відповідь: 72 літри.
Завдання 7*. Постав дужки так, щоб рівності були істинними.
(80 : 20 + 4) • 5 = 40 54 : (3 • 2) + (7 : 7) = 10
7 • (30 + 18 : 3) = 252 (80 • 4 : 4) • 6 = 480
До № 1051-1066
Завдання 1.
8 т З0 кг = 8030 кг З год 20 хв = 200 хв
3 год : 18 = 10 хв. 4 кг : 80 = 500 г
5 км 80 м = 5080 м 7 ц : 14 = 50 кг
Нагадаємо, що 1 т=1000 кг, 1 ц=100 кг, 1 кг=1000 г, 1 год=60 хв, 1 км=1000 м
8 т 30 кг = 8 т + 30 кг = 8000 кг + 30 кг = 8030 кг
3 год : 18 = 3 • 60 хв : 18 = 180 хв : 18 = 10 хв
5 км 80 м = 5 км + 80 м = 5000 м + 80 м = 5080 м
3 год 20 хв = 3 год + 20 хв = 3 • 60 хв + 20 хв = 180 хв + 20 хв = 200 хв
4 кг : 80 = 4 000 г : 80 = 500 г
7 ц : 14 = 700 кг : 14 = 700 кг : (7 • 2) = 700 кг : 7 : 2 = 100кг : 2 = 50 кг
Завдання 2. Виконай ділення і зроби перевірку.
|
- 3744| 18 36 208 14 0 144 144 0 |
- 970582| 97 97 10006 0 0 5 0 58 0 582 582 0 |
|
Перевірка: х 208 18 1664 208 3744 |
Перевірка: х 10006 97 70042 90054 970582 |
Завдання 3. Для сівби на одне поле привезли 45 мішків пшениці, а на друге — 69 мішків такої самої маси. На друге поле привезли пшениці на 1 т 920 кг більше, ніж на перше. Скільки всього кілограмів пшениці привезли на обидва поля?
Розв'язання.
Нагадаємо, що 1 т = 1000 кг, 1 т 920 кг = 1920 кг
69 – 45 = 24 (м.) – на стільки більше мішків пшениці привезли на друге поле.
1920 : 24 = 80 (кг) – кілограмів пшениці в одному мішку.
45 + 69 = 114 (м.) – всього мішків пшениці привезли.
80 • 114 = 9120 (кг) – всього кілограмів пшениці привезли на обидва поля.
Відповідь: 9120 кілограмів.
Завдання 4. З двох ділянок зібрали просо. Площа першої ділянки 7 га, а другої — на 4 га менша. Урожайність на першій ділянці становила 7 ц 80 кг з 1 га, на другій — 9 ц 20 кг. Знайди середню врожайність проса на цих ділянках.
Розв'язання.
Нагадаємо, що 1 ц = 100 кг, тому 7 ц 80 кг = 780 кг, 9 ц 20 кг = 920 кг.
7 – 4 = 3 (га) – площа другої ділянки.
7 + 3 = 10 (га) – площа двох ділянок разом.
780 • 7 = 5460 (кг) – зібрали проса з першої ділянки.
920 • 3 = 2760 (кг) – зібрали проса з другої ділянки.
5460 + 2760 = 8220 (кг) – зібрали проса з двох ділянок разом.
8220 : 10 = 822 (кг) – середня врожайність проса на ділянках.
Відповідь: 822 кілограми.
Завдання 5*. Чи завжди сума чотирицифрового числа й одноцифрового числа більша, ніж сума двох трицифрових чисел? Доведи.
1000 + 1 = 1001
999 + 999 = 1998
Ні. Наприклад, сума найменшого чотирицифрового числа і найменшого одноцифрового числа менша від суми двох найбільших трицифрових чисел.
До № 1067-1084
Завдання 1. Виконай дії письмово. Запиши значення виразів.
11 т 564 кг : 49 – 5 т 696 кг : 32 = 58 кг
|
-11564| 49 98 236 176 147 294 294 0 |
-5696| 32 32 178 249 224 256 256 0 |
-236 кг 178 кг 58 кг |
Завдання 2. Знайди площу кожної фігури за поданим планом.
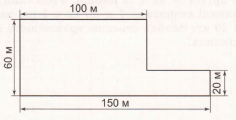
Розв'язання.
1 спосіб.
150 • 60 = 9000 (м2) – площа великого прямокутника.
(60 – 20) • (150 – 100) = 40 • 50 = 2000 (м2) – частина площі, яку треба відкинути.
9000 – 2000 = 7000 (м2) – шукана площа.
2 спосіб.
100 • 60 = 6000 (м2) – площа першої частини.
(150 – 100) • 20 = 1000 (м2) – площа другої частини.
6000 + 1000 = 7000 (м2) – шукана площа.
Відповідь: 7000 м2.
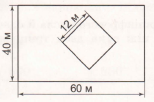
Розв'язання.
60 • 40 = 2400 (м2) – площа прямокутника.
12 • 12 = 144 (м2) – площа квадрата.
2400 – 144 = 1856 (м2) – шукана площа.
Відповідь: 1856 м2.
Завдання 3. В одному баку було 160 л води, а в другому — 190 л. Скільки літрів води треба перелити з другого баку в перший, щоб в обох баках стало води порівну? Розв'яжи задачу двома способами.
Розв'язання.
1 спосіб.
160 + 190 = 350 (л) – літрів води в двох баках.
350 : 2 = 175 (л) – стане літрів води у баках.
190 – 175 = 15 (л) – літрів води треба перелити з другого баку.
2 спосіб.
190 – 160 = 30 (л) – на стільки літрів води більше у другому баку.
30 : 2 = 15 (л) – треба відлити літрів води з другого баку.
Відповідь: 15 літрів.
Завдання 4*. Зі стосу із роздрукованим текстом випала частина сторінок. Перша сторінка цієї частини має номер 25, а номер останньої сторінки позначено тими самими цифрами, але в зворотному порядку. Скільки сторінок випало зі стосу?
Розв'язання.
Логічні задачі починай розв'язувати з малого числа. Наприклад, візьмемо з 25 по 26 сторінку. Рахуємо 25, 26 – виходить 2 сторінки. Переконалися, що треба записати вираз 52 – 25 + 1.
Номери сторінок від 25 до 52.
52 – 25 + 1 = 28
Відповідь: 28 сторінок.
До № 1085-1100
Завдання 1. Постав дужки так, щоб рівності були істинними.
((240 : 40) + 20) • 2 = 52 (90 – (З0 : 3)) • 5 = 400
(240 : (40 + 20)) • 2 = 8 (90 – З0) : 3 • 5 = 100
240 : (40 + (20 • 2)) = 3 90 – З0 : (3 • 5) = 88
240 : ((40 + 20) • 2) = 2 (90 – З0) : (3 • 5) = 4
Завдання 2. З одного поля зібрали 240 ц картоплі, а з другого — в 2 рази більше. 2/3 всієї картоплі розклали в мішки по 40 кг і завантажили їх на дві машини порівну. Скільки мішків поклали на кожну машину?
Розв'язання.
240 • 2 = 480 (кг) – зібрали картоплі з другого поля.
240 + 480 = 720 (кг) – вся картопля.
720 : 3 • 2 = 480 (кг) – узяли картоплі, щоб розкласти в мішки.
480 : 40 = 140 (м.) – вийшло мішків.
140 : 2 = 70 (м.) – мішків поклали на одну машину.
Відповідь: 70 мішків.
Завдання 3. Виконай дії письмово. Запиши значення виразу.
736 200 : 18 - 640 096 : 32 + 1948 = 22845
|
-736200| 18 72 40900 16 0 162 162 0 |
-640096| 32 64 20003 0 0 0 0 9 0 96 96 0 |
-40900 20003 20897 |
+20897 1948 22845 |
Завдання 4. Склади й розв'яжи задачу за коротким записом. Заповни схему міркувань і склади вираз.
Зібрали — ?
Вивезли — 126 ящ. по 23 кг
Залишилося — на 860 кг більше, ніж вивезли.
З поля вивезли 126 ящиків зібраних помідорів по 23 кг в кожному ящику. Скільки зібрали кілограмів помідорів, якщо залишилося на 860 кг більше, ніж вивезли.
Розв'язання.
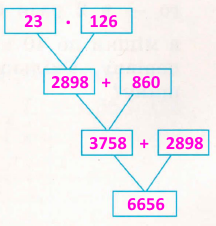
23 • 126 =2898 (кг) – вивезли кілограмів помідорів.
2898 + 860 = 3758 (кг) – залишилося кілограмів помідорів.
2898 + 3758 = 6656 (кг) – зібрали кілограмів помідорів.
Відповідь: 6656 кілограмів.
Завдання 5. Запиши всі трикутники зі стороною АМ.
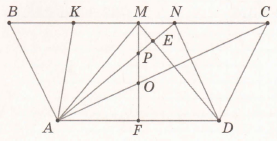
BAM, KAM, AMD, AMF, AMP, AMO, AMN, AMC
Завдання 6. Щоб викачати воду з баржі задіяли два однакових насоси. Перший працював 10 хв, а другий — 15 хв. Скільки літрів води викачали насоси, якщо другий викачав на 250 л більше, ніж перший?
Розв'язання.
1 спосіб.
15 – 10 = 5 (хв) – на стільки більше хвилин працював другий насос.
250 : 5 = 50 (л) – літрів води викачує насос за 1 хвилину.
50 • 10 = 500 (л) – літрів води викачав перший насос.
50 • 15 = 750 (л) – літрів води викачав другий насос.
500 + 750 = 1250 (л) – літрів води викачали два насоси.
2 спосіб.
15 – 10 = 5 (хв.) – на стільки більше хвилин працював другий насос.
250 : 5 = 50 (л) – літрів води викачує насос за 1 хвилину.
15 + 10 = 25 (хв) – хвилин працювали насоси.
50 • 25 = 1250 (л) – літрів води викачали два насоси.
Відповідь: 1250 літрів.
Завдання 7. Виконай обчислення за схемою, підставивши замість а число з таблиці. Отримані результати запиши в таблицю.
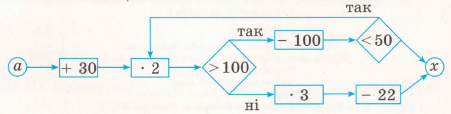
|
a |
10 |
25 |
6 |
50 |
100 |
30 |
|
x |
218 |
38 |
194 |
60 |
160 |
98 |
|
букви |
Б |
К |
М |
О |
У |
Л |
|
10 + 30 = 40 40 • 2 = 80 80 > 100 ні 80 • 3 = 240 240 – 22 = 218 х = 218 |
25 + 30 = 55 55 • 2 = 110 110 > 100 так 110 – 100 = 10 10 < 50 так 10 • 2 = 20 20 > 100 ні 20 • 3 = 60 60 – 22 = 38 х = 38 |
6 + 30 = 36 36 • 2 = 72 72 > 100 ні 72 • 3 = 216 216 – 22 = 194 х = 194 |
50 + 30 = 80 80 • 2 = 160 160 > 100 так 160 – 100 = 60 60 < 50 ні х = 60 |
100 + 30 = 130 130 • 2 = 260 260 > 100 так 260 – 100 = 160 160 < 50 ні х = 160 |
30 + 30 = 60 60 • 2 = 120 120 > 100 так 120 – 100 = 20 20 < 50 так 20 • 2 = 40 40 > 100 ні 40 • 3 = 120 120 – 22 = 98 х = 98 |
Розташуй значення х у порядку збільшення і дізнайся прізвище мореплавця, першовідкривача Південної Америки.
|
X |
38 |
60 |
98 |
160 |
194 |
218 |
|
букви |
К |
О |
Л |
У |
М |
Б |