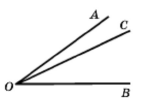
3. Промінь. Кут. Вимірювання кутів.
Проведемо пряму АВ і позначимо на ній довільну точку О, вона розбиває пряму на дві частини (кожну із цих частин разом з точкою О називають променем або пів прямою, де точку О називають початком променя). Промінь складається з точки О та всіх точок прямої АВ, що лежать по один бік від точки О, позначають ОА, ОВ (позначають промінь, називаючи дві його точки: першою обов'язково вказують початок променя, другою — будь-яку іншу точку, яка належить променю).
Означення. Два промені, які мають спільний початок і лежать на одній прямій, називають доповняльними.
Промені ОА та ОВ доповнюють один одного до прямої, тобто об'єднанням цих променів є пряма.
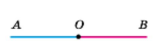
Промені ВС і ВА – доповняльні (у об'єднанні утворюють пряму, мають спільний початок), промені СА і АС не є доповняльними (у об'єднанні утворюють пряму, проте не мають спільного початку).
![]()
Два промені, що мають спільний початок, ділять площину на дві частини, які разом із променями ОА і ОВ називають кутами. Позначають ےАОВ , ےВОА, ےО (читають «кут АОВ», «кут ВОА», «кут А»), де промені ОА і ОВ називають сторонами кута, точку О – вершиною кута.
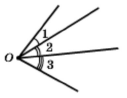
Для кілька кутів, які мають спільну вершину, позначення кута однією буквою може призвести до плутанини, тому такі кути позначають за допомогою цифр: ے1, ے 2 (читають відповідно: «кут один», «кут два»).
Для вимірювання величини кута треба вибрати одиницю виміру — одиничний кут (розділимо розгорнутий кут на 180 рівних кутів), його величину називають градусом і записують: 1°. Для отримання більш точних результатів вимірювання кутів використовують частини градуса: 1° = 60' (1 градус дорівнює 60 мінутам), 1' = 60'' (1 мінута дорівнює 60 секундам).
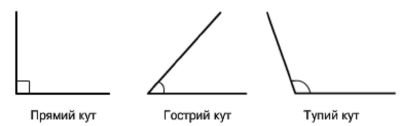
Означення. Кут, градусна міра якого дорівнює 90°, називають прямим. Кут, градусна міра якого менша від 90°, називають гострим. Кут, градусна міра якого більша за 90°, але менша від 180°, називають тупим.
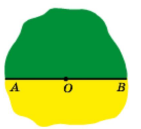
Означення. Кут, сторонами якого є доповняльні промені, називають розгорнутим (градусна міра розгорнутого кута дорівнює 180°).
Можна сказати, що розгорнутий кут — це півплощина, на межі якої позначено точку — вершину кута.
Означення. Два кути називають рівними, якщо їх можна сумістити накладанням (рівні кути мають рівні величини, і навпаки, якщо величини кутів рівні, то рівні й самі кути).
Означення. Бісектрисою кута називають промінь з початком у вершині кута, який ділить цей кут на два рівних кути.
Якщо промінь ОК — бісектриса кута АОВ, тоді ےАОК =ے КОВ.
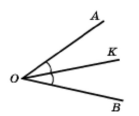
Основна властивість величини кута. Якщо промінь ОС ділить кут АОВ на два кути АОС і СОВ, то ےАОВ = ےАОС + СОВ
Надалі, говорячи «сума кутів», матимемо на увазі суму величин цих кутів.