5. Перпендикулярні прямі.

Означення. Дві прямі називають перпендикулярними, якщо при їхньому перетині утворився прямий кут. 

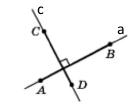
Прямі а і с перпендикулярні, пишуть а ﬩ с, с ﬩ а.

При перетині двох прямих, утворюється пара рівних гострих кутів і пара рівних тупих кутів, величину гострого кута, що утворився, називають кутом між прямими. Якщо прямі перпендикулярні, то вважають, що кут між ними дорівнює 90° (зі сказаного випливає, що кут між двома прямими не перевищує 90°).

Означення. Два відрізки називають перпендикулярними, якщо вони лежать на перпендикулярних прямих (так само можна розглядати перпендикулярність двох променів, променя та відрізка, прямої та променя, відрізка та прямої). 

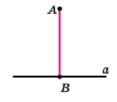
Якщо нарисувати пряму а та перпендикулярний до неї відрізок АВ, кінець якого належить прямій, у такому випадку говорять, що з точки А на пряму а опущено перпендикуляр АВ. Точку В називають основою перпендикуляра АВ.

Довжину перпендикуляра АВ називають відстанню від точки А до прямої а. Якщо точка А належить прямій а, то природно вважати, що відстань від точки А до прямої а дорівнює нулю. Нехай X — довільна точка прямої а, відмінна від точки В. Відрізок АХ називають похилою, проведеною з точки А до прямої а.

Теорема 5.1. Через кожну точку прямої проходить пише одна пряма, перпендикулярна до даної.