7. Рівні трикутники. Висота, медіана, бісектриса трикутника

Якщо три точки А, В, С, які не лежать на одній прямій, сполучити відрізками АВ, ВС, СА, тоді утворену фігуру площини разом з відрізками АВ, ВС і СА називають трикутником. Трикутник називають і позначають за його вершинами ∆АВС (читають: «трикутник АВС»), або ∆ВСА (читають: «трикутник ВСА»), або ∆АСВ (читають: «трикутник АСВ»).

Точки А, В, С називають вершинами трикутника; відрізки АВ, ВС, СА — сторонами трикутника; кути ВАС, АСВ, АВС, або А,В,С – кутами трикутника. Також, наприклад, кут В називають кутом, протилежним стороні АС; кути А,С прилеглими до сторони АС; сторону АС — стороною, протилежною куту В; сторони АВ і АС — сторонами, прилеглими до кута А. 

Означення. Периметром трикутника називають суму довжин усіх його сторін, периметр позначають буквою Р. Наприклад, РАВС.

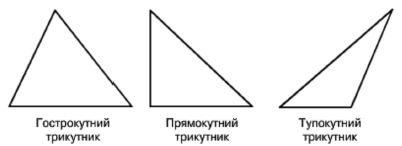
Означення. Трикутник називають гострокутним, якщо всі його кути гострі.

Трикутник називають прямокутним, якщо один із його кутів прямий. Трикутник називають тупокутним, якщо один із його кутів тупий.

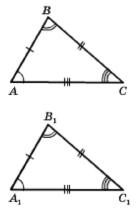
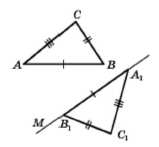
Означення. Два трикутники називають рівними, якщо їх можна сумістити накладанням.

Ті сторони й ті кути, які суміщаються при накладанні рівних трикутників, називають відповідними сторонами й відповідними кутами. Зазвичай на рисунках рівні сторони позначають однаковою кількістю рисочок, а рівні кути — однаковою кількістю дужок. В рівних трикутниках проти відповідних кутів лежать відповідні сторони, і навпаки: проти відповідних сторін лежать відповідні кути.  

Рівні трикутники АВС і А₁В₁С₁ записують так: ∆АВС = ∆А₁В₁С₁, рівні трикутники можна сумістити так, що вершини А і А₁, В і В₁, С і С₁ збігатимуться, тоді можна записати: ﮮА = ﮮА₁, ﮮВ = ﮮВ₁, ﮮС = ﮮС₁, АВ = А₁В₁, ВС = В₁С₁, СА =С₁А₁.

Основна властивість рівності трикутників. Для даного трикутника АВС і даного променя А₁М існує трикутник А₁В₁С₁, який дорівнює трикутнику АВС, такий, що АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁ і сторона А₁В₁ належить променю А₁М, а вершина С, лежить у заданій півплощині відносно прямої А₁М.

Теорема 7.1. Через точку, яка не належить даній прямій, проходить тільки одна пряма, перпендикулярна до даної.

Означення рівних відрізків, рівних кутів і рівних трикутників дуже схожі, тому доцільно прийняти таке означення рівних фігур.

Означення. Дві фігури називають рівними, якщо їх можна сумістити накладанням. 

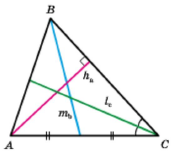
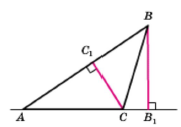
Означення. Перпендикуляр, опущений з вершини трикутника на пряму, яка містить протилежну сторону, називають висотою трикутника.

Відрізки ВВ1 і СС1 — висоти трикутника АВС.

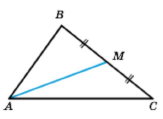
Означення. Відрізок, який сполучає вершину трикутника із серединою протилежної сторони, називають медіаною трикутника.

Відрізок АМ — медіана трикутника АВС.

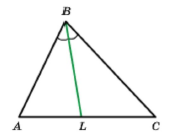
Означення. Відрізок бісектриси кута трикутника, який сполучає вершину трикутника з точкою протилежної сторони, називають бісектрисою трикутника.

Відрізок ВL — бісектриса трикутника АВС.

Кожний трикутник має три висоти, три медіани й три бісектриси.

Часто довжини сторін трикутника, протилежних кутам A, В, С, позначають відповідно а, Ь, с. Довжини висот позначають h_а, h_b, h_с, медіан — m_а, m_b, m_с, бісектрис — l_а, l_b, l_с. Індекс показує, до якої сторони проведено відрізок.