13. Паралельні прямі.

Означення. Дві прямі називають паралельними, якщо вони не перетинаються.

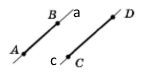
Прямі а і c паралельні, пишуть: а || c (читають: «прямі а і c паралельні» або «пряма а паралельна прямій c»).

Якщо два відрізки лежать на паралельних прямих, то їх називають паралельними. Відрізки АВ і СD паралельні, пишуть: АВ || СD.

Також можна говорити про паралельність двох променів, променя та відрізка, прямої та променя, відрізка та прямої. 

Теорема 13.1 (ознака паралельності прямих). Дві прямі, які перпендикулярні до третьої прямої, паралельні.

За допомогою лінійки та косинця можна будувати паралельні прямі.

Наслідок. Через дану точку М, яка не належить прямій а, можна провести пряму Ь, паралельну прямій а.

Основна властивість паралельних прямих (аксіома паралельності прямих). Через точку, яка не лежить на даній прямій, проходить тільки одна пряма, паралельна даній.

Теорема 13.2. Якщо дві прямі паралельні третій прямій, то вони паралельні.