П'ЯТИЙ ПОСТУЛАТ ЕВКЛІДА.
Якщо якесь твердження можна довести за допомогою аксіом або вже доведених теорем, то це твердження — теорема, а не аксіома.
Із цих позицій дуже повчальною є історія, пов'язана з п'ятим постулатом Евкліда (нагадаємо, що в оповіданні «З історії геометрії» ми сформулювали чотири перших постулати).
V постулат. І щоб кожного разу, коли пряма при перетині з двома іншими прямими утворює з ними односторонні кути, сума яких менша від двох прямих кутів, ці прямі перетиналися по той бік від січної, по який ця сума менша від двох прямих кутів.
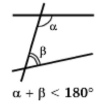
Можна показати, що п'ятий постулат і сформульована нами в п. 13 аксіома паралельності прямих рівносильні, тобто з постулату випливає аксіома, і навпаки: з аксіоми випливає постулат.
Понад двадцять століть багато вчених намагалися довести п'ятий постулат, тобто вивести його з інших аксіом Евкліда. Лише на початку XIX ст. кілька математиків незалежно один від одного дійшли висновку: твердження, що через дану точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній, є аксіомою.
Вам може здаватися, що в цьому висновку нічого особливого немає: приєднуємо аксіому паралельності до вже існуючого списку аксіом-правил, а далі доводимо теореми.
Якщо п'ятий постулат — це правило, яке ми приймаємо, а не теорема, то його можна замінити іншим правилом — твердженням, протилежним йому. Так і зробив видатний російський математик, професор Казанського університету Микола Іванович Лобачевський (1792—1856). Він замінив лише одне правило — аксіому паралельності прямих — іншим: через точку, яка не лежить на даній прямій, проходять щонайменше дві прямі, які не перетинають дану. Нова аксіома дозволила побудувати нову геометрію — неевклідову.