17. Прямокутний трикутник.

У прямокутного трикутника АВС кут АС = 90°. Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а сторони, прилеглі до прямого кута, — катетами. 

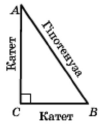
У будь-яких двох прямокутних трикутників такі елементи є завжди рівні елементи — це прямі кути, тому для прямокутних трикутників можна сформулювати «персональні» ознаки рівності.

Теорема 17.1 (ознака рівності прямокутних трикутників за гіпотенузою та катетом). Якщо гіпотенуза та катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі та катету другого, то такі трикутники рівні.

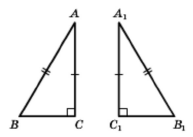
Під час розв'язування задач зручно користуватися й іншими ознаками рівності прямокутних трикутників, які безпосередньо випливають з ознак рівності трикутників.

Ознака рівності прямокутних трикутників за двома катетами. Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам другого, то такі трикутники рівні.

Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом. Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету й прилеглому до нього гострому куту другого, то такі трикутники рівні.

Очевидно, що коли гострий кут одного прямокутного трикутника дорівнює гострому куту другого прямокутного трикутника, то рівні й два інших гострих кути. Скориставшись цим твердженням, перелік ознак рівності прямокутних трикутників можна доповнити ще двома.

Ознака рівності прямокутних трикутників за катетом і протилежним гострим кутом. Якщо катет і протилежний йому гострий кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому гострому куту другого, то такі трикутники рівні.

Ознака рівності прямокутних трикутників за гіпотенузою та гострим кутом. Якщо гіпотенуза та гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту другого, то такі трикутники рівні.