19. Геометричне місце точок. Коло та круг.
Будь-яка множина точок — це геометрична фігура.
Означення. Геометричним місцем точок (ГМТ) називають множину всіх точок, які мають певну властивість.
Образно ГМТ можна подати так: задають певну властивість, а потім на білій площині усі точки, які мають цю властивість, фарбують у червоний колір. Та «червона фігура», яку при цьому отримують, і є ГМТ.
Позначимо дві точки А і В. Для всіх точок задамо властивість: одночасно належати променям АВ і ВА.Цю властивість мають усі точки відрізка АВ і тільки вони, тому відрізок АВ є ГМТ, які мають вказану властивість.

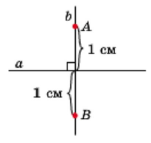
Прямі а і Ь перпендикулярні. Для всіх точок задамо властивість: належати прямій Ь і знаходитися на відстані 1 см від прямої а. Очевидно, що точки А і В задовольняють ці вимоги, а жодна точка, відмінна від А і В, цієї властивості не має. Отже, шукане ГМТ є фігурою, яка складається з двох точок А і В.
Щоб якусь множину точок можна було називати ГМТ, які мають певну властивість, треба довести дві взаємно обернені теореми:
1) пряма теорема: кожна точка даної множини має задану властивість;
2) обернена теорема: якщо точка має задану властивість. то вона належить даній множині.
Теорема 19.1. Серединний перпендикуляр відрізка є геометричним місцем точок, рівновіддалених від кінців цього відрізка.
Пряма теорема. Кожна точка серединного перпендикуляра відрізка рівновіддалена від його кінців.
Обернена теорема. Якщо точка рівновіддалена від кінців відрізка, то вона належить серединному перпендикуляру цього відрізка.
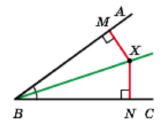
Теорема 19.2. Бісектриса кута є геометричним місцем точок, які належать куту й рівновіддалені від його сторін.
Пряма теорема. Кожна точка бісектриси кута рівновіддалена від його сторін.
Обернена теорема. Якщо точка, що належить куту, рівновіддалена від його сторін, то вона лежить на бісектрисі цього кута.
Зазначимо також, що доведена теорема справедлива й для розгорнутого кута.
Означення. Колом називають геометричне місце точок, рівновіддалених від заданої точки.
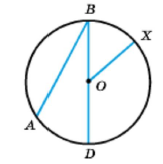
Задану точку О називають центром кола. Будь-який відрізок, який сполучає точку кола з її центром, називають радіусом кола, довжину цього відрізка також прийнято називати радіусом (відрізок ОХ — радіус). З означення випливає, що всі радіуси одного кола рівні. Відрізок, який сполучає дві точки кола, називають хордою кола (відрізки АВ і ВD — хорди). Хорду, яка проходить через центр кола, називають діаметром (відрізок ВD — діаметр кола). Діаметр кола вдвічі більший за його радіус (ВD = 2ОХ).
Фігуру, обмежену колом, називають кругом.
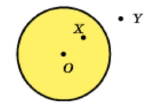
Означення. Кругом називають геометричне місце точок, відстань від яких до заданої точки не більша за дане додатне число.
Задану точку О називають центром круга. Радіус кола, яке обмежує круг, називають радіусом круга. Якщо X — довільна точка круга із центром О та радіусом R, то ОХ ≤ R. Якщо ОХ < R, то говорять, що точка X лежить усередині кола, яке обмежує даний круг. Точка Y не належить кругу, у цьому разі говорять, що точка У лежить поза колом, яке обмежує круг. З означення круга випливає, що коло, яке обмежує круг, йому належить.
Хорда й діаметр круга — це хорда й діаметр кола, яке обмежує круг.