Завдання 1. Проведіть пряму, позначте її буквою m. Позначте точки А і В, які лежать на цій прямій, і точки С, О, Е, які не лежать на ній.
Розв'язання.
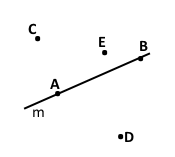
Завдання 2. Позначте точки М і К та проведіть через них пряму. Позначте на цій прямій точку Е. Запишіть усі можливі позначення отриманої прямої.
Розв'язання.
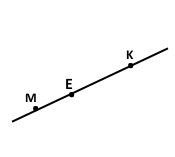
Завдання 3. Проведіть прямі а і b так, щоб вони перетиналися. Позначте точку їхнього перетину буквою С. Чи належить точка С прямій а? прямій b?
Розв'язання.
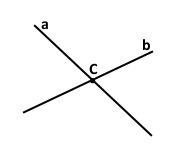
Точка С належить прямій a, точка С належить прямій b.
Завдання 4. Позначте три точки так, щоб вони не лежали на одній прямій, і через кожну пару точок проведіть пряму. Скільки утворилося прямих?
Розв'язання.
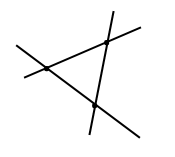
Три прямих.
Завдання 5. Позначте чотири точки, жодні три з яких не лежать на одній прямій.
Розв'язання.
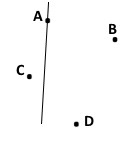
Позначили конкретну пряму і 3 точки, що не лежать на ній
У цілому, якщо позначити 4 точки, то через будь-які дві точки завжди можна провести пряму, тому поза лежатимуть тільки 2 точки.
Завдання 6. Проведіть три прямі так, щоб кожні дві з них перетиналися. Позначте точки перетину цих прямих. Скільки можна отримати точок перетину?
Розв'язання.

Три точки.
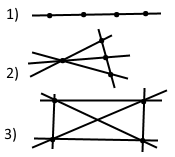
Завдання 7. Позначте чотири точки так, щоб при проведенні прямої через кожні дві з них на рисунку: 1) утворилася одна пряма; 2) утворилися чотири прямі; 3) утворилися шість прямих. Проведіть ці прямі.
Розв'язання.
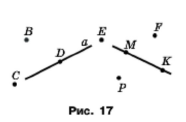
Завдання 8. Користуючись рисунком 17:
1) визначте, чи перетинаються прямі а і МК;
2) укажіть усі позначені точки, які належать прямій а; прямій МК;
3) укажіть усі позначені точки, які не належать прямій а; прямій МК;
4) укажіть усі позначені точки, які належать прямій а, але не належать прямій МК.
Розв'язання.
1) Так, в точці Е
2) С, D, E
3) B, M, K, F
4) C, D
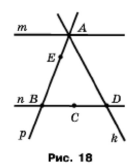
Завдання 9. Користуючись рисунком 18, укажіть:
1) які з позначених точок належать прямій р, а які не належать їй;
2) яким прямим належить точка А; точка В; точка С; точка D; точка Е;
3) які прямі проходять через точку С; точку В; точку А;
4) у якій точці перетинаються прямі k і р; прямі m і k;
5) у якій точці перетинаються три із чотирьох зображених на рисунку прямих.
Розв'язання.
1) належать прямій р точки В, Е, А; не належать C, D
2) точка А належить прямим m, p , k; точка В належить прямим n, p; точка С належить прямій n; точка D належить прямим n, k ; точка Е належить прямій p.
3) через точку С проходить пряма n; через точку В проходять прямі n,p; через точку А проходять прямі m,p,k
4) прямі k i p перетинаються в точці A; прямі m i k перетинаються в точці A
5) три прямих перетинаються в точці А
Завдання 10. Точка С належить прямій АВ. Чи є різними прямі АВ і АС? Відповідь обґрунтуйте.
Розв'язання.
Точка А і С належать прямій АВ, а через дві точки можна провести одну пряму, тому прямі АВ і АС не можуть бути різними.
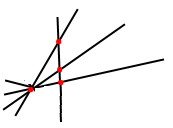
Завдання 11. Провели чотири прямі, кожні дві з яких перетинаються, причому через кожну точку перетину проходять тільки дві прямі. Скільки точок перетину при цьому утворилося?
Розв'язання.
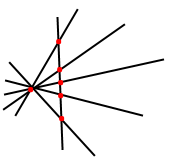
Завдання 12. Як треба розташувати шість точок, щоб вони визначали шість прямих?
Розв'язання.
Завдання 13. Дану пряму перетинають чотири прямі. Скільки може утворитися точок перетину цих прямих з даною?
Розв'язання.
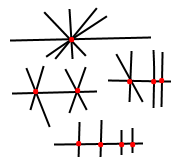
Одна, дві, три, чотири точки.
Завдання 14. Провели чотири прямі, кожні дві з яких перетинаються. Скільки точок перетину може утворитися?
Розв'язання.
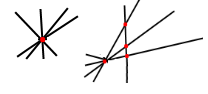
1 точка, 4 точки.
Завдання 15. Провели п'ять прямих, кожні дві з яких перетинаються. Яка найменша можлива кількість точок перетину цих прямих? Яка найбільша кількість точок перетину може утворитися?
Розв'язання.

Найменша кількість точок 1, найбільша кількість точок 10.
Завдання 16. Чи можна провести шість прямих і позначити на них 11 точок так, щоб на кожній прямій було позначено рівно чотири точки?
Розв'язання.
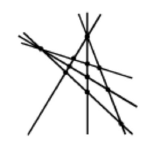
Завдання 17. На площині проведено три прямі. На першій прямій позначили п'ять точок, на другій — сім точок, а на третій — три точки. Яка найменша кількість точок може бути позначена?
Розв'язання.
Найменша кількість точок буде, коли три прямі перетинаються у 3 точках, тоді точок буде 12.
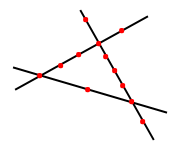
Завдання 18. Чи можна позначити кілька точок і провести кілька прямих так, щоб на кожній прямій лежало рівно три позначені точки й через кожну точку проходило рівно три з проведених прямих?
Розв'язання.
Так.
Завдання 19. Правильність виготовлення лінійки можна перевірити так. Через дві точки за допомогою лінійки провести лінію. Потім лінійку перевернути і через ті самі точки вздовж того самого краю лінійки знову провести ще одну лінію. Якщо лінії збігатимуться, то лінійку виготовлено правильно. Поясніть чому.
Розв'язання.
Прямі збігатимуться, бо через дві точки можна провести лише одну пряму.
Завдання 20. Складіть квадрат із кількох фігур, кожна з яких дорівнює фігурі, зображеній на рисунку 19.
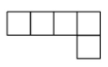
Розв'язання.
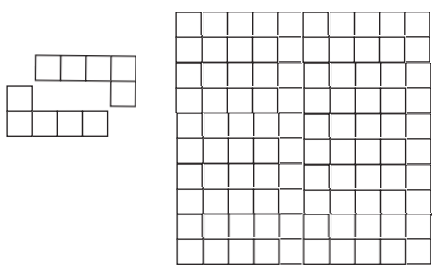
Скласти "блок" розміром 5 квадратів на 2 квадрати і взяти їх десять разів як на рисунку.