Завдання 33
Точка К — середина відрізка МN, точка Е — середина відрізка КN, ЕN = 5 см. Знайдіть відрізки MК, МЕ і МN.
Розв'язання.
![]()
MK = KN = 2 EN = 2 • 5 = 10 (см)
ME = MK + KE = KN + EN = 2EN + EN = 3EN = 3 • 5 = 15 (см)
MN = 2KN = 2 • (2EN) = 4EN = 4 • 5 = 20 (см)
Завдання 34
На папері в клітинку позначено точки A, B і C (рис. 38). Знайдіть відстань від точки C до середини відрізка AB, якщо довжина сторони клітинки дорівнює 5 мм.
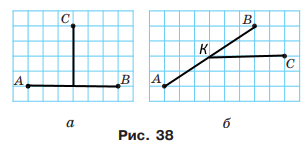
Розв'язання
а) СК = 2 см; б) СК = 2,5 см
Завдання 35
На папері в клітинку позначено точки M, N і K (рис. 39). Знайдіть відстань від точки M до середини відрізка NK, якщо довжина сторони клітинки дорівнює 5 мм.

Розв'язання
а) МА = 1,5 см; б) МА = 1,5 см
Завдання 36
Точка C — внутрішня точка відрізка AB, довжина якого дорівнює 20 см. Знайдіть відрізки AC і BC, якщо:
1) відрізок AC на 5 см більший за відрізок BC;
Розв'язання
Нехай відрізок ВС дорівнює х см, тоді АС – (х + 5) см. За умовою С – внутрішня точка, тоді АВ = АС + ВС = 20 см. Складаємо рівняння:
х + (х + 5) = 20
2х = 15
х = 15 : 2
х = 7,5 (см) – довжина відрізка ВС;
7,5 + 5 = 12,5 (см) – довжина відрізка АС.
Відповідь: 12,5 см; 7,5 см.
2) відрізок AC у 4 рази менший від відрізка BC;
Розв'язання
Нехай відрізок АС дорівнює х см, тоді ВС – 4х см. За умовою С – внутрішня точка, тоді АВ = АС + ВС = 20 см. Складаємо рівняння:
х + 4х = 20
5х = 20
х = 20 : 5
х = 4 (см) – довжина відрізка АС;
4 • 4 = 16 (см) – довжина відрізка ВС.
Відповідь: 4 см; 16 см.
3) AC : BC = 9 : 11.
Розв'язання
Нехай k – коефіцієнт пропорційності, тоді АС дорівнює 9k см, а ВС – 11k см. За умовою С – внутрішня точка, тоді АВ = АС + ВС = 20 см. Складаємо рівняння:
9k + 11k = 20
20k = 20
k = 20 : 20
k = 1
1 • 9 = 9 (см) – довжина відрізка АС.
1 • 11 = 11 (см) – довжина відрізка ВС.
Відповідь: 9 см; 11 см.
Завдання 37
Точка K належить відрізку CD, довжина якого дорівнює 28 см. Знайдіть відрізки CK і KD, якщо:
1) відрізок CK на 4 см менший від відрізка KD;
Розв'язання
Нехай відрізок CK дорівнює х см, тоді KD – (х + 4) см. За умовою К – внутрішня точка, тоді CD = CK + KD = 28 см. Складаємо рівняння:
х + (х + 4) = 28
2х = 24
х = 24 : 2
х = 12 (см) – довжина відрізка CK;
12 + 4 = 16 (см) – довжина відрізка KD.
Відповідь: 12 см; 16 см.
2) відрізок CK у 6 разів більший за відрізок KD;
Розв'язання
Нехай відрізок KD дорівнює х см, тоді CK – 6х см. За умовою К – внутрішня точка, тоді CD = CK + KD = 28 см. Складаємо рівняння:
х + 6х = 28
7х = 28
х = 28 : 7
х = 4 (см) – довжина відрізка KD;
4 • 6 = 24 (см) – довжина відрізка CK.
Відповідь: 4 см; 24 см.
3) CK : KD = 3 : 4.
Розв'язання
Нехай k – коефіцієнт пропорційності, тоді CK дорівнює 3k см, а KD – 4k см. За умовою К – внутрішня точка, тоді CD = CK + KD = 28 см. Складаємо рівняння:
3k + 4k = 28
7k = 28
k = 28 : 7
k = 4
4 • 3 = 12 (см) – довжина відрізка CK.
4 • 4 = 16 (см) – довжина відрізка KD.
Відповідь: 12 см; 16 см.
Завдання 38
Відрізки АВ і СD рівні (рис. 40). Доведіть, що відрізки AC і BD теж рівні.
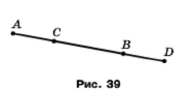
Розв'язання.
Оскільки точка С внутрішня точка відрізка АВ, тоді АВ = АС + СВ; оскільки точка В внутрішня точка відрізка CD, тоді CD = CB + BD. За умовою АС + СВ = СВ + BD, тобто АС = СВ + BD – CB = BD, що треба було довести.
Завдання 39
Відрізки МЕ і FN рівні (рис. 41). Доведіть, що МF = EN.
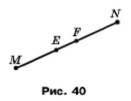
Розв'язання.
За умовою маємо MF = FN. Оскільки точка Е внутрішня точка відрізка MF, тоді MF = ME + EF; оскільки точка F внутрішня точка відрізка EN, тоді EN = EF + FN. Тоді треба довести, що MF – EN = 0. Маємо, ME + EF – (EF + FN) = ME + EF – EF – FN = ME – FN = ME – ME = 0, що треба було довести.
Задвдання 40
Точка С ділить відрізок АВ, довжина якого дорівнює а, на два відрізки. Знайдіть відстань між серединами відрізків АС і ВС.
Розв'язання.
Оскільки точка С внутрішня точка середина відрізка АВ, тоді АС = ВС = а/2. Довжина половини відрізків АС ( відповідно ВС) дорівнює а/4, тому відстань між серединами відрізків АС і ВС дорівнює 2 • а/4 = а/2
Завдання 41
Точки А, В і С лежать на одній прямій. Знайдіть відрізок ВС, якщо АВ = 24 см, АС = 32 см. Скільки розв'язків має задача?
Розв'язання.
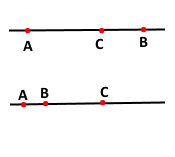
Задача має два розв'язки. Розглянемо перший випадок. АВ = АС + СВ = 24 + 32 = 56 (см); у другому випадку АС = АВ + ВС, тоді ВС = АС – АВ = 32 – 24 = 8 (см)
Завдання 42
На прямій позначено точки А, В і С так, що АВ = 15 см, АС = 9 см. Знайдіть відстань між серединами відрізків.
Розв'язання.
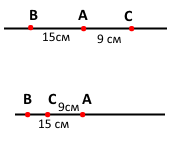
Задача має два розв'язки. У першому випадку відстань між серединами відрізків дорівнюватиме 1/2ВА + 1/2АС = ½ (ВА + АС) = ½ (15 + 9) = 12 (см). У другому випадку середина відрізка ВА = 15 : 2 = 7,5 (см), середина відрізка СА = 9 : 2 = 4,5 (см). Очевидно, що відстань між серединами даних відрізків дорівнюватиме 7,5 – 4, 5 = 3 (см).
Завдання 43
Відрізок ЕF дорівнює 12 см. Знайдіть на прямій ЕF усі точки, сума відстаней від кожної з яких до кінців відрізка ЕF дорівнює: 1) 12 см; 2) 15 см; 3) 10 см.
Розв'язання.
1) усі точки відрізка.
2) нема таких точок на прямій, оскільки такі точки лежать поза прямою.
3) нема таких точок.
Завдання 44
Через точки А і В проведено пряму. Де на цій прямій лежить точка С, відстань від якої до точки В у 2 рази більша, ніж відстань від неї до точки А?
Розв'язання.
АС = 1/3 АВ
Завдання 45
Відрізок, довжина якого дорівнює 32 см, поділили на три нерівних відрізки. Відстань між серединами крайніх відрізків дорівнює 18 см. Знайдіть довжину середнього відрізка.
Розв'язання.
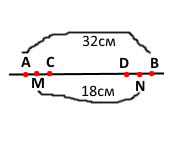
AB – MN = AM + NB , оскільки М – середина відрізка АС, N – середина відрізка DB, тоді AM = MC, DN = NB, CD = MN – (MC + DN) = MN – (AM + NB) = MN – (AB - MN) = 18 – (32 – 18) = 18 – 14 = 4 (см).
Завдання 46
Скільки точок треба позначити між точками А і В, щоб разом з відрізком АВ утворилося шість відрізків?
Розв'язання.
5 точок.
УЧИМОСЯ ЗАСТОСОВУВАТИ ГЕОМЕТРІЮ
Завдання 47
Порівняйте на око відрізки АВ і CD (рис. 42). Перевірте свій висновок вимірюванням.
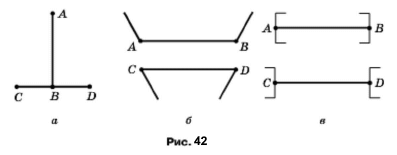
Розв'язання.
Рівні.
Завдання 48
Порівняйте на око відрізки АВ і ВС (рис. 43). Перевірте свій висновок вимірюванням.
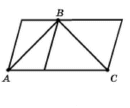
Розв'язання.
Рівні.
Завдання 49
На шкалі лінійки нанесено тільки поділки 0 см, 5 см і 13 см. Як, користуючись цією лінійкою, можна побудувати відрізок завдовжки: 1) 3 см; 2) 2 см; 3) 1 см?
Розв'язання.(+ відкладаємо відрізок від точки лівого кінця вправо, - відкладаємо відрізок від точки правого кінця вліво).
1) 13 см – 5 см – 5см = 3см
2) 5см + 5см + 5см – 13см = 2см
3) 13см + 13см – 5см – 5см – 5см = 1см
Завдання 50
На шкалі лінійки нанесено тільки поділки 0 см, 7 см і 11 см. Як, користуючись цією лінійкою, можна побудувати відрізок завдовжки: 1) 8 см; 2) 5 см?
Розв'язання. (+ відкладаємо відрізок від точки лівого кінця вправо, - відкладаємо відрізок від точки правого кінця вліво).
1) 11см + 11см – 7см – 7см = 8см
2) 11см + 11см + 7см + 11см – 7см – 7см – 7см – 7см – 7см = 5см
СПОСТЕРІГАЙТЕ, РИСУЙТЕ, КОНСТРУЮЙТЕ, ФАНТАЗУЙТЕ
Завдання 51
Із прямокутників розмірами 1x1, 1x2, 1x3, ..., 1x13 складіть прямокутник, кожна сторона якого більша за 1.