Завдання 52
Проведіть два промені АВ і АС так, щоб вони не були доповняльними. Побудуйте до кожного із цих променів доповняльний промінь. Позначте й запишіть усі утворені промені.
Розв'язання
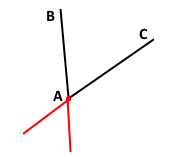
Завдання 53
Проведіть відрізок АВ і два промені АВ і ВА. Чи є ці промені доповняльними? Відповідь обґрунтуйте.
Розв'язання
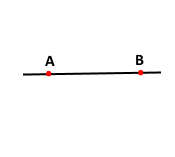
Промені не є доповняльними, оскільки не мають спільного початку.
Завдання 54
Накресліть кут МNЕ і проведіть промені NA і NC між його сторонами. Запишіть усі кути, що утворилися.
Розв'язання
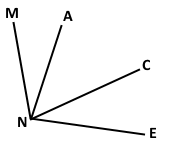
Кути MNA, MNC, ANC, ANE, CNE
Завдання 55
Проведіть промені ОА, ОВ, ОС і ОD так, щоб промінь ОС проходив між сторонами кута AОВ, а промінь ОD — між сторонами кута ВОС.
Розв'язання
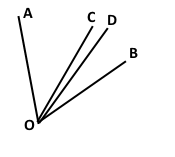
Завдання 56
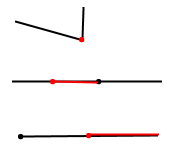
Накресліть два промені так, щоб їхня спільна частина була: 1) точкою; 2) відрізком; 3) променем.
Розв'язання
Завдання 57
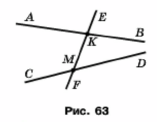
Пряма ЕР перетинає прямі АВ і СD (рис. 66). Укажіть:
1) усі промені, що утворилися, з початком у точці М;
2) усі пари доповняльних променів з початком у точці К.
Розв'язання
1) MC, MF, MD, MK, ME
2) KA i KB, KE i KF
Завдання 58
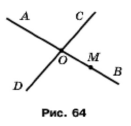
Запишіть усі промені, які зображено на рисунку 67. Укажіть, які з них є доповняльними променями з початком у точці О.
Розв'язання
OA i OB, OC i OD
Завдання 59
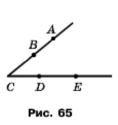
Чи можна кут, який зображено на рисунку 68, позначити так:
1) ∠АВС; 3) ∠АDC; 5) ∠АСЕ; 7) ∠ВDЕ;
2) ∠АСD; 4) ∠DСА; 6) ∠ВСD; 8) ∠ЕСD?
Розв'язання
1) ні 3) ні 5) так 7) ні
2) так 4) так 6) так 7) ні
Задача 60
Запишіть усі кути, які зображено на рисунку 69.
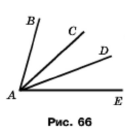
Розв'язання
Кути BAC, BAD, BAE, CAD, CAE, DAE
Завдання 61
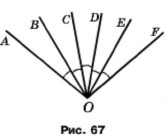
На рисунку 70 ∠AОВ = ∠ВОС = ∠СОD = ∠DOЕ = ∠ЕОF.
1) Який промінь е бісектрисою кута АОС? кута DOF? кута ВОF?
2) Бісектрисою яких кутів є промінь ОС?
Розв'язання
Промінь OB є бісектрисою кута AOC
Промінь OC є бісектрисою кутів BOD, AOE
Промінь OD є бісектрисою кутів COE, BOF
Промінь OE є бісектрисою кутів DOF
Завдання 62
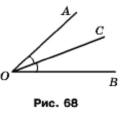
Промінь OC — бісектриса кута AOB (рис. 71). Чи можна сумістити накладанням: 1) кути AOC і BOC; 2) кути AOC і AOB?
Розв'язання
1) так 2) ні
Завдання 63
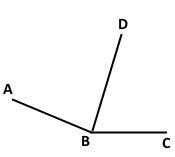
Промінь ВD ділить кут AВС на два кути. Знайдіть:
1) кут AВС, якщо ∠АВD = 54°, ∠СВD = 72°;
2) кут СВD, якщо ∠AВС = 158°, ∠AВD = 93°.
Розв'язання
1) ∠АВС = ∠ABD + ∠CBD = 54° + 72° = 126°
2) ∠CBD = ∠ABC – ∠ABD = 158° – 93° = 65°
Завдання 64
Промінь ОР проходить між сторонами кута МОК. Знайдіть кут МОР, якщо ∠МОK = 172°, ∠РОК = 85°.
Розв'язання
За основною властивістю величини кута маємо ∠MOK = ∠MOP + ∠POK, тоді ∠MOP = ∠MOK – ∠POK = 172° – 85° = 87°
Завдання 65
Величина кута дорівнює: 1) 28°; 2) 162°. Яка величина кута, утвореного бісектрисою даного кута і його стороною?
Розв'язання
Бісектриса ділить кут на два рівні кути, тому величина кута, утвореного бісектрисою даного кута і його стороною дорівнює:
1) 28° : 2 = 14°
2) 162° : 2 = 81°
Завдання 66
Знайдіть кут, бісектриса якого утворює з однією з його сторін кут, який дорівнює: 1) 43°; 2) 65°.
Розв'язання
Бісектриса ділить кут на два рівні кути, тому величина кута дорівнює:
1) 43° • 2 = 86°
2) 65° • 2 = 130°
Завдання 67 Чи правильне твердження:
1) будь-який кут, менший від тупого, — гострий;
2) кут, менший від розгорнутого, — тупий;
3) кут, менший від тупого у 2 рази, — гострий;
4) сума двох гострих кутів більша за прямий кут;
5) кут, менший від розгорнутого кута у 2 рази, є більшим за будь-який гострий кут;
6) кут, більший за прямий, — тупий?
Розв'язання
1) ні (може бути гострим, прямим)
2) ні (може бути гострим, тупим, прямим)
3) так
4) ні
5) такий кут є прямим, він більший за будь-який гострий.
Завдання 68
Кут СЕF дорівнює 152°, промінь ЕМ проходить між його сторонами, кут СЕМ на 18° більший за кут FЕМ. Знайдіть кути СЕМ і FЕМ.
Розв'язання
За основною властивістю величини кута ∠CEF = ∠CEM + ∠FEM, нехай х – величина кута FEM, тоді х + 18 – величина кута CEM, складемо рівняння
x + (x + 18) = 152
2x + 18 = 152
2x = 152 – 18
2x = 134
x = 134 : 2
x = 67
∠FEM = 67°, ∠CEM = 67° + 18° = 85°
Завдання 69
Промінь АК належить куту ВAD. Знайдіть кути ВАК і DАК, якщо кут ВАК у 7 разів менший від кута DАК і ∠ВАD = 72°.
Розв'язання
За основною властивістю величини кута ∠BAD = ∠BAK + ∠DAK, нехай х – величина кута DAK, тоді 7х – величина кута BAK, складемо рівняння
x + 7x = 72
8x = 72
x = 72 : 8
x = 9
∠DAK = 9°, ∠BAK = 9° • 7 = 63°
Завдання 70
На рисунку 72 рівні кути позначено дужками. Знайдіть кути АВС, МКЕ і SТК, якщо за одиничний кут узято: 1) кут АВС; 2) кут МКЕ.
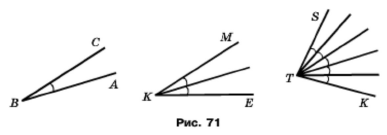
Розв'язання.
1) ABC = 1од., MKE = 2од., STK = 5од.
2) ABC = ½ од., KME = 1од., STK = 2½ од.
Завдання 71
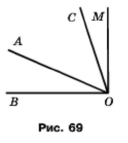
Із вершини прямого кута ВОМ (рис. 73) проведено два промені ОA та ОС так, що ∠ВОС = 74°, ∠AОМ = 62°. Знайдіть кут AОС.
Розв'язання
∠COM = ∠BOM – ∠BOC = 90° – 74° = 16°, тоді ∠AOC = ∠AOM – ∠COM = 62° – 16° = 46°
Завдання 72
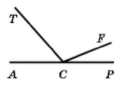
Із вершини розгорнутого кута АСР (рис. 74) проведено два промені СТ і СF так, що ∠АСF = 158°, ∠ТСР = = 134°. Знайдіть кут ТСF.
Розв'язання
Розгорнутий кут ∠ACP = 180°, ∠TCF = ∠ACP – ∠ACT – ∠FCP = ∠ACP – (∠ACP - ∠TCP) – (∠ACP –∠ ACF) = ∠ACP – ∠ACP + ∠TCP – ∠ACP + ∠ACF =∠ TPC + ∠ACF – ∠ACP = 134° + 158° - 180 ° = 112°
Завдання 73
Точки А, В і С розміщено на прямій так, що АВ = 3,2 см, АС = 4,8 см, ВС = 8 см. Чи є промені АВ і АС доповняльними?
Розв'язання.
За основною властивістю довжин відрізка для внутрішньої точки А маємо ВС = ВА + АС = АВ + АС = 3,2см + 4,8см = 8см. Точки В, А, С лежать на одній прямій, промені АВ і АС мають спільний початок, тому промені АВ і АС є доповняльними.
Завдання 74
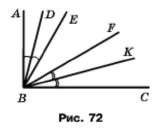
На рисунку 75 кут АВС прямий, ∠АВЕ = ∠ЕВF = ∠FВС, промені BD і ВК — бісектриси кутів АВЕ і FВС відповідно. Знайдіть кут DВК.
Розв'язання
За основною властивістю величини кута маємо ∠ABC = ∠ABE + ∠EBF + ∠FBC = 3∠EBF, тоді ∠EBF = ∠ABC : 3 = 90° : 3 = 30°, а ∠DBK = ∠ABC – ∠ADB – ∠KBC. Оскільки для рівних кутів BD бісектриса кута ABE , BK бісектриса кута FBC, то ∠ABD = ∠KBC = ½ ∠ABE = 30° : 2 = 15°, ∠DBK = 90° – 15° – 15° = 60°.