Завдання 75
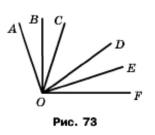
На рисунку 76 ےАОС = ےСОD = ےDOF, промінь ОВ — бісектриса кута AОС, промінь ОЕ — бісектриса кута DОF, ےВОЕ = 72°. Знайдіть кут AОF.
Розв'язання
Оскільки кути рівні, а ОВ і ОЕ бісектриси рівних кутів, тоді ےAOB + ےBOC = ےAOC = ےCOD = ےDOF + ےEOF = ےDOF = ےBOC + ےDOE, ےBOE = 2COD, ےAOB + ےEOF = ےCOD = ½ ےBOE, ےAOF = ےAOB + ےBOE + ےEOF = ½ ےBOE + ےBOE = 72°: 2 + 72° = 108°
Завдання 76
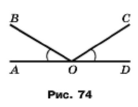
На рисунку 77 ےAОВ = ےDОС. Чи є ще на цьому рисунку рівні кути? Відповідь обґрунтуйте.
Розв'язання
Маємо ےAOB = ےCOD ,треба довести, що ےAOC = ےBOD, тобто ےAOC – ےBOD = 0, оскільки ےAOC = ےAOB + ےBOC, ےBOD = ےBOC + ےCOD, тоді ےAOC – ےBOD = ےAOB + ےBOC – (ےBOC + ےCOD) = ےAOB + ےBOC – ےBOC – ےCOD = ےAOB – ےCOD = 0, що треба було довести. Значить ےAOC = ےBOD.
Завдання 77
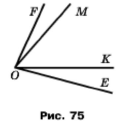
Кути FОК і МОЕ рівні (рис. 78). Чи рівні кути FОМ і КОЕ?
Розв'язання
Маємо ےFOK = ےMOE, треба довести ےFOM = ےKOE, тобто ےFOM – ےKOE = 0. За основною властивістю величини кута ےFOK = ےFOM + ےMOK, ےMOE = ےMOK + ےKOE, тоді ےFOM – ےKOE = (ےFOK – ےMOK) – (ےMOE – ےMOK) = ےFOK – ےMOK – ےMOE + ےMOK = ےFOK – ےMOE = 0, що й треба було довести. Значить кути рівні.
Завдання 78
Промінь ВК є бісектрисою кута СВD, ےАВК = 146° (рис. 79). Знайдіть кут СВD.
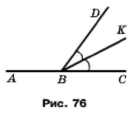
Розв'язання
Оскільки ВК – бісектриса кута CBD, то ےCBD = 2 ےKBC = 2 • (ےABC – ےABK) = 2 • (180° – 146°) = 68°
Завдання 79
Промінь ВК є бісектрисою кута СВD, ےСВD = 56° (рис. 79). Знайдіть кут AВК.

Розв'язання
Оскільки ВК – бісектриса кута CBD, то ےCBK = ½ ےCBD = 56° : 2 = 28°, ےABK = ےABC – ےCBK = (180° – 28°) = 152°
Завдання 80
На скільки градусів повертається за 1 хв: 1) хвилинна стрілка; 2) годинна стрілка?
Розв'язання
1) Оскільки повний оберт хвилинна стрілка робить за 1 год = 60хв, тому за 1 хв вона повернеться на 360° : 60 = 6°
2) 6° : 60 = 1/10°
Завдання 81
Знайдіть кут між стрілками годинника, якщо вони показують: 1) 3 год; 2) 6 год; 3) 4 год; 4) 11 год; 5) 7 год.
Розв'язання
Стрілка робить повний оберт за 12год, тому за 1год кут між стрілками 360° : 12 = 30°.
1) 30° • 3 = 90°
2) 30° • 6 = 180°
3) 30° • 4 = 120°
4) 30° • 11 = 330°
5) 30° • 7 = 210°
Завдання 82
Кут AВС дорівнює 30°, кут СВD — 80°. Знайдіть кут АВD. Скільки розв'язків має задача?
Розв'язання
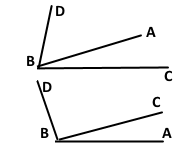
Задача має два розв'язки. У першому випадку ےABD = ےCBD – ےABC = 80° - 30° = 60°. У другому випадку ےABD = ےABC + ےCBD = 30° + 80° = 110°
Завдання 83
Знайдіть кут МОК, якщо ےMON = 120°, ےKON = 43°. Скільки розв'язків має задача?
Розв'язання
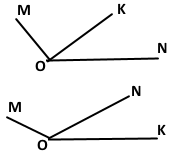
Задача має два розв'язки. У першому випадку ےMOK = ےMON – ےKON = 120° - 43° = 77°. У другому випадку ےMOK = ےKON + ےMON = 43° + 120° = 163°
Завдання 84
Промінь, проведений з вершини прямого кута, ділить його на два кути. Доведіть, що кут між бісектрисами кутів, що утворилися, дорівнює 45°.
Розв'язання
![]()
Оскільки ОС бісектриса кута СОЕ, то СОЕ = АОС = ½ АОЕ, оскільки OD i OB бісектриси рівних кутів COE i AOC , тому COD + BCO = ½ COE + ½ AOC = ½ (COE + AOC) = ½ AOE = ½ • 90° = 45°
Завдання 85
Як, маючи шаблон кута, що дорівнює 70°, побудувати кут, який дорівнює 40°?
Розв'язання
7g_m_u2015_03__080
180° - 70° - 70° = 40°
Завдання 86
Як, маючи шаблон кута, що дорівнює 40°, побудувати кут, який дорівнює: 1) 80°; 2) 160°; 3) 20°?
Розв'язання
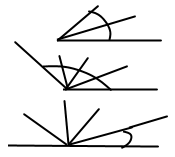
1) 40° + 40° = 80°
2) 40° + 40° + 40° + 40° = 160°
3) 180° - 40° - 40° - 40° - 40° = 20°
Завдання 87
Як, використовуючи шаблон кута, що дорівнює 13°, побудувати кут, який дорівнює 2°?
Розв'язання
13° • 14 - 180° = 182° - 180° = 2°
Послідовно 14 разів відкласти шаблон кута, до першої сторони кута добудувати доповняльний промінь (провести пряму, на якій лежить перша сторона). Кут між доповняльним променем та другою стороною кута і буде шуканим.
Завдання 88
Як побудувати кут, який дорівнює 1°, використовуючи шаблон кута, що дорівнює: 1) 19°; 2) 7°?
Розв'язання
1) 19 разів відкласти шаблон кута 19° (19° • 19 – 360° = 1°)
2) 13 разів відкласти шаблон кута 7°, до першої сторони кута провести перпендикуляр через вершину кута, шуканим буде кут між перпендикуляром і другою стороною кута (7° • 13 – 90° = 1°).
Завдання 89
Проведіть шість прямих, що перетинаються в одній точці. Чи правильно, що серед кутів, які при цьому утворилися, є кут, який менший від 31°?
Розв'язання.
Так, оскільки 6 прямих утворить 12 променів зі спільною вершиною, тоді 360° : 12 = 30°.
УЧИМОСЯ ЗАСТОСОВУВАТИ ГЕОМЕТРІЮ
Завдання 90
Південний вітер змінився на: 1) західний; 2) південносхідний. Знайдіть кут, на який змінився напрямок вітру.
Розв'язання
1) південний напрямок становить 180°, а західний – 90°, тому кут 180° – 90° = 90°
2) південний напрямок становить 180°, а південносхідний - 135°, тому кут 180° – 135° = 45°
Завдання 91
Дув північний вітер. Потім його напрямок змінився на кут: 1) 90°; 2) 45°. Яким після цього став вітер?
Розв'язання
1) північний напрямок становить 0°, а кут змінився на 90° (0° + 90° = 90°), тому вітер став східним або західним.
2) північний напрямок становить 0°, а кут змінився на 45° (0° + 45° = 45°), тому вітер став північно-західним або північно-східним.
СПОСТЕРІГАЙТЕ, РИСУЙТЕ, КОНСТРУЮЙТЕ, ФАНТАЗУЙТЕ
Завдання 92
Не відриваючи олівця від паперу, проведіть через дев'ять точок (рис. 80) чотири відрізки (повертатися у вихідну точку не обов'язково).

Розв'язання