Завдання 93
Накресліть три кути: гострий, прямий і тупий. Для кожного з них побудуйте суміжний кут.
Розв'язання
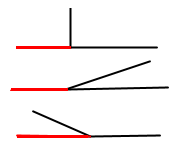
Завдання 94
Накресліть два нерівних суміжних кути так, щоб їхня спільна сторона була вертикальною.
Розв'язання
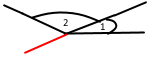
Завдання 95
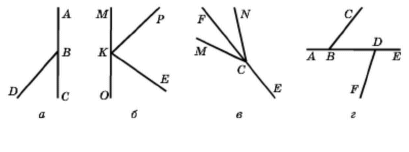
Укажіть пари суміжних кутів (рис. 86).
Розв'язання
а) CBD і DBA
б) MKP і PKO; OKE і EKM
в) FCN і NCE; FCM і MCE
г) ABC і CBE; ADF і FDE
Завдання 96
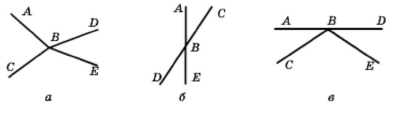
Чи є кути АВС і DВЕ вертикальними (рис. 87)?
Розв'язання
а) ні б) так в) ні
Завдання 97
Скільки пар суміжних кутів зображено на рисунку 88? Назвіть їх. Укажіть пари вертикальних кутів.
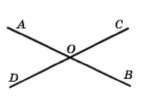
Розв'язання.
Пари суміжних кутів DOA і AOC; COB і DOD.
Пари вертикальних кутів AOD і COB; AOC і DOB.
Завдання 98
Чи можуть два суміжних кути дорівнювати: 1) 24° і 156°; 2) 63° і 107°? Відповідь обґрунтуйте.
Розв'язання
За теоремою про суму суміжних кутів перевіримо.
1) так, оскільки 24° + 156° = 180°
2) ні, оскільки 63° + 107° < 180°
Завдання 99
Знайдіть кут, суміжний із кутом: 1) 29°; 2) 84°; 3) 98°; 4) 135°.
Розв'язання
За теоремою про суму суміжних кутів маємо
1) 180° – 29° = 151°
2) 180° – 84° = 96°
3) 180° – 98° = 82°
4) 180° – 135° = 45°
Завдання 100
Чи може пара суміжних кутів складатися:
1) із двох гострих кутів;
2) із двох тупих кутів;
3) із прямого та тупого кутів;
4) із прямого та гострого кутів?
Розв'язання
1) ні
2) ні
3) ні
4) ні
Завдання 101
Один із суміжних кутів — прямий. Яким є другий кут?
Розв'язання
За теоремою про суму суміжних кутів випливає 180° – 90° = 90°, тобто другий кут є також прямим.
Завдання 102
Знайдіть кут, суміжний із кутом АВС, якщо: 1) ےАВС = 36°; 2) ےАВС = 102°.
Розв'язання
За теоремою про суму суміжних кутів маємо кут величину суміжного кута.
1) 180° – 36° = 144°
2) 180° – 102° = 78°
Завдання 103
Знайдіть кути 2, 3 і 4 (рис. 89), якщо кут 1 дорівнює 42°
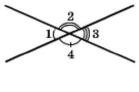
Розв'язання
Оскільки кути 1 і кут 3 вертикальні, то вони рівні, тобто ∠1 = ∠3 = 42 °. Кути 1 і 2 є суміжними, тому ∠2 = 180 ° – ∠1 = 180 ° –∠42 ° = 138 °. Кути 2 і 4 вертикальні, тому вони рівні, тобто ∠4 = ∠2 = 138 °
Завдання 104
Знайдіть суміжні кути, якщо:
1) один із них на 70° більший за другий;
Нехай величина меншого кута дорівнює х градусів, тоді величина більшого кута – (х + 70) градусів. Складаємо рівняння згідно теореми про суму суміжних кутів:
х + х + 70 = 180
2х + 70 = 180
2х = 110
х = 110 : 2
х = 55 (°) – величина меншого кута;
55 + 70 = 125 (°) – величина більшого кута.
Відповідь: 125° і 55°.
2) один із них у 8 разів менший від другого;
Нехай величина меншого кута дорівнює х градусів, тоді величина більшого кута – 8х градусів. Складаємо рівняння згідно теореми про суму суміжних кутів:
х + 8х = 180
9х = 180
х = 180 : 9
х = 20 (°) – величина меншого кута;
20° • 8 = 160 (°) – величина більшого кута.
Відповідь: 20° і 160°.
3) їхні градусні міри відносяться як 3 : 2.
Нехай коефіцієнт пропорційності дорівнює k, тоді величина першого кута 3k, а величина другого – 2k. Складемо рівняння згідно теореми про суму суміжних кутів:
3k + 2k = 180
5k = 180
k = 180 : 5
k = 36
36 • 3 = 108 (°) – величина першого кута;
36 • 2 = 72 (°) – величина другого кута.
Відповідь: 108° і 72°.
Завдання 105
Знайдіть суміжні кути, якщо:
1) один із них у 17 разів більший за другий;
Нехай величина другого кута х (°), тоді величина першого кута – 17х (°). Складемо рівняння згідно теореми про суму суміжних кутів:
х + 17х = 180
18х = 180
х = 180 : 18
х = 10 (°) – величина другого кута;
10° • 17 = 170 (°) – величина першого кута.
Відповідь: 170° і 10°.
2) їхні градусні міри відносяться як 19 : 26.
Нехай коефіцієнт пропорційності дорівнює k, тоді величина першого кута 19k, а величина другого – 26k. Складемо рівняння згідно теореми про суму суміжних кутів:
19k + 26k = 180
45k = 180
k = 180 : 45
k = 4
4 • 19 = 76 (°) – величина першого кута;
4 • 26 = 104 (°) – величина другого кута.
Відповідь: 76° і 104°.
Завдання 106
Чи є правильним твердження:
1) для кожного кута можна побудувати тільки один вертикальний кут; Так
2) для кожного кута можна побудувати тільки один суміжний кут; Ні (не справджується для розгорнутого кута)
3) якщо кути рівні, то вони вертикальні; Ні
4) якщо кути не рівні, то вони не вертикальні; Так
5) якщо кути не вертикальні, то вони не рівні; Ні
6) якщо два кути суміжні, то один із них гострий, а другий — тупий; Ні
7) якщо два кути суміжні, то один із них більший за другий; Ні (бо не справджується для прямокутних суміжних кутів)
8) якщо сума двох кутів дорівнює 180°, то вони суміжні; Ні (суміжні кути мають мати спільну вершину та сторону)
9) якщо сума двох кутів не дорівнює 180°, то вони не суміжні; Так
10) якщо суміжні кути рівні, то вони прямі; Так
11) якщо рівні кути мають спільну вершину, то вони вертикальні; Ні (сторони одного кута мають бути доповняльними променями другого кута)
12) якщо два кути мають спільну сторону, то вони суміжні? Ні