Завдання 107
Доведіть, що коли два кути рівні, то й суміжні з ними кути рівні.
Розв'язання
Завдання 108
Сума двох кутів, утворених при перетині двох прямих, дорівнює 140°. Доведіть, що ці кути вертикальні.
Розв'язання
При перетині двох прямих утворюються дві пари суміжних та дві пари вертикальних кутів. Це не можуть бути суміжні кути, оскільки сума кутів менша за 180°, значить це вертикальні кути.
Завдання 109
Знайдіть кути, які утворюються при перетині двох прямих, якщо:
1) сума двох із них дорівнює 106°;
2) сума трьох із них дорівнює 305°.
Розв'язання
1) Оскільки сума двох кутів не дорівнює 180°, то два кути вертикальні, вони рівні, величина яких дорівнює 106° : 2 = 53°. Інший кут є суміжним , тому величина кожного кута іншої пари вертикальних кутів дорівнює 180° – 53° = 127°
2) Величина третього кута та відповідного вертикального для нього кута 360° – 305° = 57°, тоді величина двох інших вертикальних кутів дорівнює 180° – 57° = 123°
Завдання 110
Знайдіть кути, які утворюються при перетині двох прямих, якщо різниця двох із них дорівнює 64°.
Розв'язання
При перетині двох прямих прямих утворюється 2 пари рівних вертикальних кутів, нехай х – величина кута з першої пари, тоді х + 64 – величина кута з другої пари, два вертикальні кути різних пар утворюють суміжний кут. Cкладемо рівняння:
х + х + 64 = 180
2х = 180 – 64
2х = 116
х = 116 : 2
х = 58
При перетині двох прямих утворюються два кути по 58°, та два кути по 58° + 64° = 122°.
Завдання 111
Три прямі перетинаються в одній точці (рис. 90). Знайдіть ∠1 + ∠2 + ∠3.
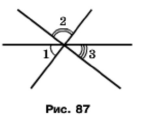
Розв'язання
При перетині трьох прямих утворюються три пари вертикальних кутів, оскільки вертикальні кути рівні, маємо ∠1 + ∠2 + ∠3 = 180°
Завдання 112
Прямі AВ, СD і МК перетинаються в точці О (рис. 91), ∠АОС = 70°, ∠МОВ = 15°. Знайдіть кути DОК, АОМ і АОD
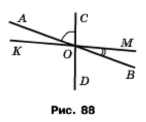
Розв'язання
Вертикальні кути рівні, тому ∠MOB = ∠AOK = 15°, ∠AOC = ∠BOD = 70°, ∠DOK = ∠COM. За основною властивістю величини кута
∠DOK = ∠COM = ∠AOB – ∠AOC – ∠MOB = 180° – 15° – 70° = 95°,
∠AOM = ∠AOB – ∠MOB = 180° – 15° = 165°, ∠AOD = ∠COD – ∠AOC = 180° – 70° = 110°
Завдання 113
Знайдіть кут між бісектрисами суміжних кутів.
Розв'язання
Оскільки бісектриса ділить кут навпіл, а сума суміжних кутів дорівнює 180°, то кут між бісектрисами дорівнює 180° : 2 = 90°
Завдання 114
Знайдіть кут між бісектрисами вертикальних кутів.
Розв'язання
Кут між бісектрисами вертикальних кутів утворює розгорнутий кут, тому дорівнює 180°
Завдання 115
Кути АВF і FВС суміжні, ∠АВF = 80°, промінь ВD належить куту АВF, ∠АВD = 30°. Знайдіть кут між бісектрисами кутів DВF і FВС.
Розв'язання
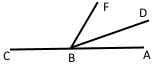
За основною властивістю величини кута маємо ∠DBF = ∠ABF – ∠ABD = 80° – 30° = 50°. За теоремою про суму суміжних кутів маємо ∠FBC = ∠CBA – ∠ABF = 180° – 80° =100°. Кут між бісектрисами кутів DBF і FBC дорівнює:
½ ∠DBF + ½ ∠FBC = ½ (∠DBF + ∠FBC) = ½ (50° + 100°) = 75°
Завдання 116
Кути АОВ і ВОС суміжні, промінь ОD — бісектриса кута АОВ, кут ВОD на 18° менший від кута ВОС. Знайдіть кути АОВ і ВОС.
Розв'язання
Нехай х – величина кута ВОD, тоді х + 18 – величина кута ВОC, оскільки OD – бісектриса кута АОВ, тоді ∠АОВ = 2∠BOD, за теоремою про суму суміжних кутів ∠AOB + ∠BOC = 180°, складемо рівняння:
х + х + (х + 18) = 180
3х + 18 = 180
3х = 180 – 18
3х = 162
х = 162 : 3
х = 54
∠AOB = 2∠BOD = 54° • 2 = 108°, ∠BOC = 54° + 18° = 72°
Завдання 117
Знайдіть суміжні кути МКЕ і РКЕ, якщо кут FКЕ на 24° більший за кут РКЕ, де промінь КF — бісектриса кута МКЕ.
Розв'язання
Нехай х – величина кута PKE, тоді х + 24 – величина кута FKE, оскільки KF – бісектриса кута MKE, тоді ∠MKE = 2∠FKE, за теоремою про суму суміжних кутів ∠MKE + ∠PKE = 180°, складемо рівняння:
(х + 24) + (х + 24) + x = 180
3х + 48 = 180
3х = 180 – 48
3х = 132
х = 132 : 3
х = 44
∠PKE = 44 °, ∠MKE = 2∠FKE = (44° + 24°) • 2 = 136°
Завдання 118
На рисунку 92 ∠МAВ + ∠АСВ = 180°. Доведіть, що ∠МАВ = ∠КСВ.
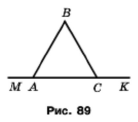
Розв'язання
Доведемо, що MAB – KCB = 0.
З умови маємо ∠MAB = 180° – ∠ACB, для суміжних кутів ∠ACB + ∠KCB = 180°,
тоді ∠MAB – ∠KCB = (180° – ∠ACB) – ∠KCB = 180° – (∠ACB + ∠KCB) =
= 180° – 180° = 0°, що й треба було довести.
Завдання 119
На рисунку 93 ∠МВС = ∠ВЕF. Доведіть, що ∠АВЕ + ∠ВЕD = 180°.
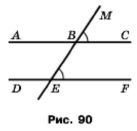
Розв'язання
Вертикальні кути рівні ∠MBC = ∠ABE, суміжний кут ∠BED = 180° – ∠BEF = 180° – ∠MBC,
тоді ∠ABE + ∠BED = ∠MBC + (180° – ∠MBC) = 180°, що треба було довести.
Завдання 120
Два кути мають спільну сторону, а їхня сума дорівнює 180°. Чи можна стверджувати, що ці кути є суміжними?
Розв'язання
Ні. ∠АОВ і ∠ВОС мають спільну сторону ∠ОВ і ∠АОВ + ∠ВОС = 120° + 60° = 180°, але ∠АОВ і ∠ВОС не є суміжними.
Завдання 121
Розріжте фігуру, зображену на рисунку 94, на шість частин двома прямими.