Завдання 122
Перерисуйте в зошит рисунок 102. Користуючись косинцем, проведіть через точку М пряму, перпендикулярну до прямої а.
Розв'язання

Завдання 123
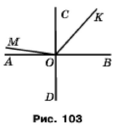
Перерисуйте в зошит рисунок 103. Користуючись косинцем, опустіть із точки M перпендикуляр на пряму a. Проведіть із точки M які‒небудь дві похилі до прямої a.
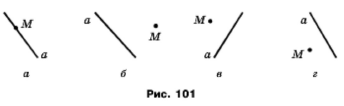
Завдання 124
Проведіть пряму с і позначте на ній точку К. Користуючись косинцем, проведіть через точку К пряму, перпендикулярну до прямої с.
Розв'язання
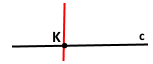
Завдання 125
Проведіть пряму d і позначте точку M, яка їй не належить. За допомогою косинця опустіть із точки M перпендикуляр на пряму d. Проведіть із точки M які‒небудь дві похилі до прямої d.
Розв'язання
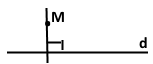
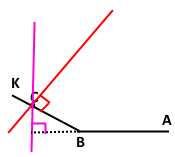
Завдання 126
Накресліть кут АВК, який дорівнює: 1) 73˚; 2) 146˚. Позначте на промені ВК точку С і проведіть через неї прямі, перпендикулярні до прямих АВ і ВК.
Розв'язання
| 1) 73˚; | 2) 146˚ |
 |
 |
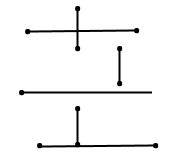
Завдання 127
Накресліть два перпендикулярних відрізки так, щоб вони: 1) перетиналися та не мали спільного кінця; 2) не мали спільних точок; 3) мали спільний кінець.
Розв'язання
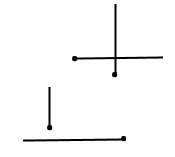
Завдання 128
Накресліть два перпендикулярних промені так, щоб вони: 1) перетиналися; 2) не мали спільних точок.
Розв'язання
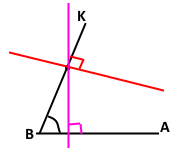
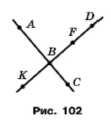
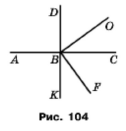
Завдання 129
На рисунку 104 прямі АС і DК перпендикулярні. Чи перпендикулярні:
Розв'язання
1) відрізки АВ і ВК; Так
2) відрізки ВС і DF; Так
3) промені ВС і ВК; Так
4) відрізок АВ і промінь FD? Так
Завдання 130
Чи може кут між прямими дорівнювати: 1) 1˚; 2) 80˚; 3) 90°; 4) 92°; 5) 101°?
Розв'язання
При перетині двох прямих, утворюється пара рівних гострих кутів і пара рівних тупих кутів, величину гострого кута, що утворився, називають кутом між прямими. Зі сказаного випливає, що кут між двома прямими не перевищує 90°.
1) так
2) так
3) ні
4) ні
Завдання 131
Назар накреслив дві прямі, які перетинаються, за допомогою транспортира визначив, що один із кутів, утворених при перетині прямих, дорівнює 110°, і сказав, що кут між цими прямими становить 110°. Чи має рацію Назар? Відповідь обґрунтуйте.
Завдання 132
Прямі EF і MK перетинаються в точці A, ∠EAK = 142° (рис. 105). Знайдіть кут між прямими EF і MK.
Завдання 133
Вважаючи, що довжина сторони клітинки дорівнює 0,5 см, знайдіть відстань від точки M до прямої AB (рис. 106).
Завдання 134
Вважаючи, що довжина сторони клітинки дорівнює 0,5 см, знайдіть відстань від точки O до прямої CD (рис. 107).
Завдання 135
Доведіть, що коли бісектриси кутів АОВ і ВОС перпендикулярні, то точки А, О і С лежать на одній прямій.
Розв'язання
Якщо бісектриси кутів АОВ і ВОС перпендикулярні, тоді вони утворюються двома кутами по 45°. Значить кут АОВ = ВОС = 90°, а промені ОА та ОВ утворюють розгорнутий кут, значить точки А,О,С лежать на одній прямій.
Завдання 136
На рисунку 108 АВ ⊥ СD, ∠СОК = 42˚, ∠МОК ⊥ ∠ВОК = 130°. Знайдіть: 1)∠МОК; 2)∠МОD.
Розв'язання
1) ∠BOK = ∠COB – ∠COK = 90° ‒ 42° = 48°, ∠MOK = 130° ‒ ∠BOK = 130° ‒ 48° = 82°
2) ∠MOD = ∠MOA ⊥ ∠AOD, ∠MOA = ∠АОВ – (∠МОК ⊥ ∠ВОК) = 180° ‒ 130° = 50°,
∠MOD = 90° ⊥ 50° = 140°
Завдання 137
На рисунку 109 АС ⊥ DК, ОВ ⊥ ВF, ∠DВО = 54°. Знайдіть кут АВF.
Розв'язання
∠ABF = ∠ABK ⊥ ∠KBF, ∠KBF = ∠KBD – ∠DBO – ∠OBF = 180° ‒ 54° ‒ 90° = 36°,
∠ABF = 90° ⊥ 36° = 126°
Завдання 138
Кут АВС дорівнює 160°, промені ВК і ВМ проходять між сторонами цього кута й перпендикулярні до них. Знайдіть кут МВК.
Розв'язання
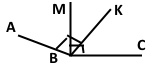
∠ABC = ∠ABK ⊥ ∠CBK, ∠ABC = ∠ABK ⊥ (∠MBC ‒ ∠MBK),
∠MBK = ∠ABK ⊥ ∠MDC – ∠ABC = 90° ⊥ 90° ‒ 160° = 20°
Завдання 139
На рисунку 110 ВF ⊥ АС, ВD ⊥ ВК. Доведіть, що ∠ABD = ∠FВК.
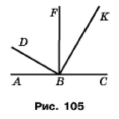
Розв'язання
За основною властивістю величини кута
∠ABD = ∠ABC ‒ ∠DBK – ∠CBK = 180° ‒ 90° ‒ ∠CBK = 90° ‒ ∠CBK, a
∠FBK = ∠ABC – ∠ABF – ∠CBK = 180° ‒ 90° ‒ ∠CBK = 90° ‒ ∠CBK, тобто ∠ABD = ∠FBK, що й треба було довести.
Завдання 140
На рисунку 110 ∠AВD = ∠FВК, ∠DВF = ∠KВС. Доведіть, що ВF ⊥ АС.

Розв'язання
Якщо прямі ВF ⊥ АС, тоді треба довести, що ∠ABF = 90°.
Розгорнутий кут ∠АВС = 180°. За основною властивістю величини кута маємо
∠ABC = ∠ABD ⊥ ∠DBF ⊥ ∠FBК ⊥ ∠КВС = 2∠АВD ⊥ 2∠DBF = 2 (∠ABD ⊥ ∠DBF), звідси
∠ABF = ∠ABD ⊥ ∠DBF = ∠ABC : 2 = 180° : 2 = 90°, тобто прямі ВF ⊥ АС.
Завдання 141
Із вершини кута АВС, який дорівнює 70°, проведено промені ВD і ВF так, що ВD ⊥ ВА, ВF ⊥ ВС, промені ВD і ВF належать куту AВF. Знайдіть кути DВF і AВF.
Розв'язання.
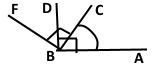
Розв'язання
1 спосіб
∠ABF = ∠FBC ⊥ ∠ABC = 90° ⊥ 70° = 160°, ∠DBF = ∠ABF – ∠ABD = 160° ‒ 90° = 70°.
2 спосіб
∠FBA = ∠FBC ⊥ ∠ABC = 90° ⊥ ∠ABC, ∠FBA = ∠ABD ⊥ ∠FBD = 90° ⊥ ∠FBD, звідси випливає, що ∠FBD = ∠ABC = 70°. ∠FBA = ∠FBD ⊥ ∠ABD = 70° ⊥ 90° = 160°
Завдання 142
Із вершини кута ABC, який дорівнює 130°, проведено промені BD і BF так, що BD ⊥ AB, BF ⊥ BC, промінь BF належить куту ABC, промінь BA належить куту DBF. Знайдіть кут DBF
Розв'язання
Завдання 143
Користуючись косинцем і шаблоном кута, який дорівнює 17°, побудуйте кут, який дорівнює: 1) 5°; 2) 12°.
Розв'язання
1) 90° ‒ 17° • 5 = 5°
2) 17° • 6 ‒ 90° = 12°
Завдання 144
Користуючись косинцем і шаблоном кута, який дорівнює 20˚ побудуйте кут, який дорівнює 10°.
Розв'язання.
90° ‒ 20° • 4 = 10°
Завдання 145
Прикладаючи косинець то однією, то іншою стороною, Марія провела через точку A два перпендикуляри до прямої a (рис. 111). Що можна сказати про цей косинець?
Розв'язання
Завдання 146
На рисунку 112 пряма перетинає всі сторони восьмикутника. Чи може пряма перетинати всі сторони тринадцятикутника, не проходячи через жодну з його вершин?
