Задача 146. Які з елементів трикутника — бісектриса, медіана, висота — завжди належать трикутнику?
Розв'язання.
Бісектриса.
Задача 147. Який з елементів трикутника — бісектриса, медіана, висота — може збігатися з його стороною? Укажіть вид трикутника, для якого це можливо.
Розв'язання.
У прямокутника висота збігається із стороною.
Задача 148. 1) Чи може одна висота трикутника належати йому,
а дві інші — ні?
2) Чи може тільки одна висота трикутника збігатися з його стороною?
3) У якому трикутнику три висоти перетинаються в його вершині?
Розв'язання.
1) так, у тупокутника.
2) ні (бо висоти збігаються з двома сторонами у прямокутнику).
3) у прямокутнику.
Задача 149. Медіана BD трикутника AВС розбиває його на два трикутники, периметри яких дорівнюють 32 см і 36 см. Знайдіть периметр трикутника АВС, якщо ВD = 10 см.
Розв'язання.
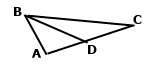
Розглянемо суму двох периметрів 32см + 36см = (AB + BD + AD) + (BC + DC + BD). Периметр шуканого трикутника AB + BC + AD + DC = 32см + 36см – 2BD = 32см + 36см – 20см = 38 см
Задача 150. Медіана трикутника, периметр якого дорівнює 60 см, розбиває його на два трикутники, периметри яких дорівнюють 36 см і 50 см. Чому дорівнює довжина цієї медіани?
Розв'язання.

Розглянемо суму двох периметрів 36см + 50см = (AB + BD + ½ AC) + (BC + ½ AC + BD). Периметр великого трикутника AB + BC + ½ AC + ½ AC = 32см + 36см – 2BD , звідси знайдемо медіану BD, тобто
60 = 36 + 50 – 2BD
2BD = 36 + 50 – 60
2BD = 26
BD = 26 : 2
BD = 13
Довжина медіани BD = 13 см
Задача 151. На рисунку 123 КР = РЕ = ЕF = FТ = 1 см. Які рівні відрізки є ще на цьому рисунку? Знайдіть їхні довжини.

Розв'язання.
KE = PF = ET = 2см
KF = PT = 3см
Задача 152. Промінь ВD розбиває кут АВС, який дорівнює 72˚, на два кути АВD і СВD так, що ﮮАВD = 5 ﮮСВD. Промінь ВК проходить так, що промінь ВA є бісектрисою кута DВК. Визначте градусну міру та вид кута DВК.
Розв'язання.
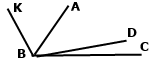
Кут АВD = ABC : 6 • 5 = 72˚ : 6 • 5 = 60˚, оскільки промінь ВА бісектриса кута DBK, тоді тупий кут DBK = 2 ABD = 60˚ • 2 = 120˚
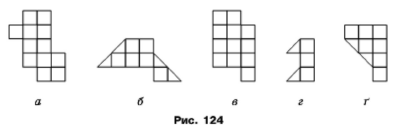
Задача 153. Розріжте кожну з фігур, зображених на рисунку 124, на дві рівні фігури (розрізати не обов'язково вздовж ліній сітки).