Задача 154. За допомогою лінійки та транспортира побудуйте трикутник, дві сторони якого дорівнюють 3 см і 6 см, а кут між ними — 40˚.
Розв'язання.
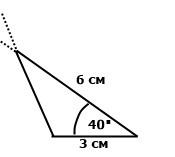
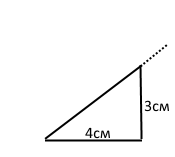
Задача 155. За допомогою лінійки та транспортира побудуйте трикутник, дві сторони якого дорівнюють 3 см і 4 см, а кут між ними — 90˚. Укажіть вид цього трикутника.
Розв'язання.
Прямокутник.
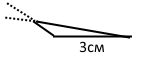
Задача 156. За допомогою лінійки та транспортира побудуйте трикутник, одна сторона якого дорівнює 3 см, а кути, що прилягають до цієї сторони, — 100˚ і
20°. Укажіть вид цього трикутника.
Розв'язання.
Тупокутник.
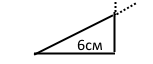
Задача 157. За допомогою лінійки та транспортира побудуйте трикутник, одна сторона якого дорівнює 6 см, а кути, що прилягають до цієї сторони, — 90° і 45°.
Розв'язання.
Задача 158. Перерисуйте в зошит рисунок 131. За допомогою косинця та лінійки знайдіть на прямій l точку, рівновіддалену від кінців відрізка AВ.
7g_m_u2015_08_158
Розв'язання.
7g_m_u2015_08__158
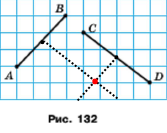
Задача 159. Перерисуйте в зошит рисунок 132. За допомогою косинця та лінійки знайдіть точку, яка рівновіддалена від точок А і В та водночас рівновіддалена від точок С і D.
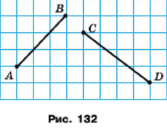
Розв'язання.
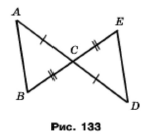
Задача 160. На рисунку 133 АС = ОС, ВС = ЕС. Доведіть, що ∆AВС = ∆DЕС.
Розв'язання.
За умовою дві відповідні сторони рівні АС = ОС, ВС = ЕС, а вертикальні кути теж рівні ےАСВ = ےDCE, тому за двома сторонами і кутом між ними трикутники рівні ∆AВС = ∆DЕС.
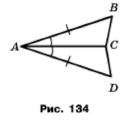
Задача 161. На рисунку 134 AВ = AD, ﮮВАС = ﮮDАС. Доведіть, що ∆AВС = ∆ADС.
Розв'язання.
За умовою відповідні сторони АB = AD та кути ﮮВАС = ﮮDАС рівні, сторона АС спільна для двох трикутників , тому за двома сторонами і кутом між ними трикутники рівні ∆AВС = ∆АDС.
Задача 162. На рисунку 135 АВ = СD, ﮮ1 = ﮮ2, AD=7 см, ﮮС = 34°. Знайдіть відрізок ВС і кут А.
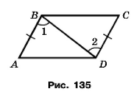
Розв'язання.
За умовою відповідні сторони АB = AD та кути ﮮ1 = ﮮ2 рівні, сторона BD спільна для двох трикутників , тому за двома сторонами і кутом між ними трикутники рівні ∆AВС = ∆АDС. У рівних трикутників відповідні сторони та кути рівні, тому ےА = ےС = 34°, ВС = AD = 7см.
Задача 163. На рисунку 136 АО = ОD, ВО = ОС. Знайдіть сторону СD і кут ОСD трикутника ОСD, якщо AВ = 8 см, ﮮОВА = 43°.
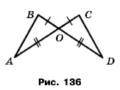
Розв'язання.
За умовою дві відповідні сторони АО = ОD, ВО = ОС, а вертикальні кути рівні ےAOB = ےDOC, тому за двома сторонами і кутом між ними трикутники рівні ∆ОВА = ∆ОСD. У рівних трикутників відповідні сторони та кути рівні, тому СD = AB = 8см, OCD = OBA = 43°.
Задача 164. Дано: ОА = ОС, ОВ = ОD (рис. 137). Доведіть, що ﮮОАD =
= ﮮOCB
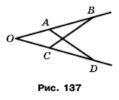
Розв'язання.
За умовою дві відповідні сторони ОА = ОС, ОВ = ОD, а кут О спільний для двох трикутників , тому за двома сторонами і кутом між ними трикутники рівні ∆OAD = ∆OCB, у рівних трикутників рівні відповідні кути, отже, ﮮОАD = ﮮOCB.
Задача 165. Дано: ﮮАDС =ﮮАDВ, ВD=СD (рис. 138). Доведіть, що АВ = АС.
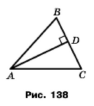
Розв'язання.
За умовою відповідні сторони ВD=СD та кути ﮮАDС =ﮮАDВ рівні , а сторона AD спільна для двох трикутників , тому за двома сторонами і кутом між ними трикутники рівні ∆ABD = ∆ACD, у рівних трикутників рівні сторони рівні, отже, AB = AC.
Задача 166. Із точок А і В, які лежать в одній півплощині відносно прямої а на однаковій відстані від неї, опущено на цю пряму перпендикуляри АС і ВD. Знайдіть кут АСВ, якщо ﮮАDС = 25°.
Розв'язання.
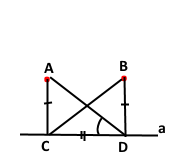
Оскільки через точку, яка не належить даній прямій, проходить тільки одна пряма, перпендикулярна до даної, а точки однаково віддалені від прямої, то AC = BD, а кути прямі ACD = BDC = 90° та спільна сторона CD, за двома сторонами та кутом між ними ΔACD = ΔBDC. У рівних трикутників рівні відповідні кути ے BCD = ے ADC. За основною властивістю величини кута ےACB = ے ACD – ے BCD = 90° - 25° = 65°.
Задача 167. Відрізки АD і ВС перетинаються в точці О та діляться цією точкою навпіл. Знайдіть кут АСD, якщо ﮮАВС = 64˚, ﮮАСО = 56°.
Розв'язання.
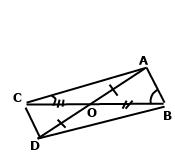
За умовою точка О ділить відрізки AD і ВС на рівні частини, тобто OC = OB, OD = OA. Вертикальні кути рівні ےCOD = ےBOA. За двома сторонами та кутом між ними трикутники рівні ∆COD = ∆BOA. У рівних трикутників рівні відповідні кути ےDCO = ےABO = ےABC, тому ےACD = ےACO + ےOCD = ےACO + ےABC = 64˚ + 56˚ = 120˚.
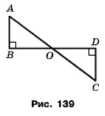
Задача 168. На рисунку 139 АВ ﬩ ВО, СD ﬩ ВD, точка О — середина відрізка ВD. Доведіть, що ∆АВО = ∆СDO.
Розв'язання.
За умовою АВ ﬩ ВО, СD ﬩ ВD , значить ﮮАВО =ﮮCDO = 90°. Оскільки О – середина відрізка BD, то за основною властивістю довжини відрізка BD = BO + OD, BO = OD. Вертикальні кути рівні ےAOB = ےCOD, тому за стороною і прилеглими кутами трикутники рівні ∆АВО = ∆СDO.