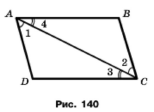
Задача 169. На рисунку 140 ﮮ1 = ﮮ 2, ﮮ 3 = ﮮ 4, АВ = 8 см, ВС = 6 см. Знайдіть сторони AD і СD трикутника АDС.
Розв'язання.
За умовою ﮮ1 = ﮮ 2, ﮮ 3 = ﮮ 4, а сторона АС спільна, тому трикутники рівні за стороною і прилеглими кутами. У рівних трикутників відповідні сторони і кути рівні, тому AD = BC = 6 см, AB = CD = 8 см.
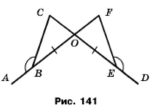
Задача 170. На рисунку 141 ﮮ AВС = ﮮ DEF, ВО=ОЕ. Доведіть, що ∆ВСО = ∆ЕFО.
Розв'язання.
За умовою у трикутника рівні сторони BO = OE. Вертикальні кути рівні ﮮ COB = ﮮ FOE. Доведемо, що ﮮ CBO = ﮮ FEO, для цього переконаємось, що різниця цих кутів дорівнює 0. ﮮ CBO – ﮮ FEO = (180˚ - ﮮ ABC) – (180˚ - ﮮ DEF) = ﮮ DEF – ABC = 0˚. За стороною та двома прилеглими кутами ∆ВСО = ∆ЕFО.
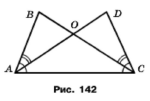
Задача 171. На рисунку 142 ﮮ ВАО = ﮮ DСО, ﮮ ВАС = ﮮ DСА. Доведіть, що ∆AВС = ∆CDA.
Розв'язання.
За умовою ﮮ ВАС = ﮮ DСА, сторона АС спільна. За умовою ﮮ ВАО = ﮮ DСО, ﮮ ВАС = ﮮ DСА, тобто ﮮ ВАО - ﮮ DСО = 0˚, ﮮ ВАС - ﮮ DСА = 0˚. Залишається довести, що ےDAC = ےBCA. Покажемо, що різниця кутів дорівнює нулю. Справді, ےDAC – ےBCA = (ےBAC - ےBAO) – (ےDCA – ےDCO) = (ےBAC – ےDAC) + (BAO – DCO) = 0˚
Задача 172. На сторонах кута з вершиною в точці В позначено точки А і С, а на його бісектрисі — точку D таку, що ﮮ АDВ = ﮮ СDВ. Доведіть, що АВ = ВС.
Розв'язання.
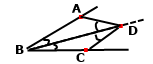
Розглянемо трикутники BAD і BCD. За умовою ﮮ АDВ = ﮮ СDВ , точка D лежить на бісектрисі кута АВС, тому ﮮ ABD = ﮮ DBC. Сторона BD спільна для двох трикутників, тому за стороною та прилеглими кутами трикутники рівні. У рівних трикутників рівні відповідні сторони АВ = ВС.
Задача 173. Через точку М, яка належить бісектрисі кута з вершиною в точці О, проведено пряму, яка перпендикулярна до цієї бісектриси. Ця пряма перетинає сторони даного кута в точках А і В. Доведіть, що АМ = МВ.
Розв'язання.
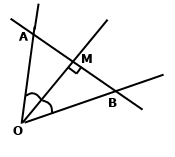
Розглянемо трикутники АМО і ВМО. За умовою пряма АВ ﬩ ОМ, тому ﮮ ВМО = ﮮ АМО = 90˚, ОМ – бісектриса кута АОВ, тому ﮮ АОМ = ﮮ ВОМ. Сторона ОМ спільна для двох трикутників, тому за стороною та прилеглими кутами трикутники рівні. У рівних трикутників відповідні сторони рівні АМ = МВ.
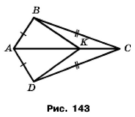
Задача 174. На рисунку 143 ∆AВС = ∆АDС. Доведіть, що ∆АВК = = ∆АDК.
Розв'язання.
За умовою ∆AВС = ∆АDС, тому АВ = АD, ﮮ BAC = ﮮ DAC. Сторона АК спільна для обох трикутників АВК і АDК, тому за двома сторонами та кутом між ними ∆АВК = = ∆АDК.
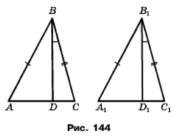
Задача 175. На рисунку 144 ∆АВС = ∆A1B1C1, ﮮ DВС = ﮮ D1D1С1. Доведіть, що ∆DВС=∆D1В1С1.
Розв'язання.
Оскільки ∆АВС = ∆A1B1C1, то відповідні кути рівні ﮮ АСВ = ﮮ А1С1В1, відповідні сторони теж ВС = В1С1. Розглянемо трикутники DВС і D1В1С1. За умовою ﮮ DВС = ﮮ D1D1С1, тому за стороною ВС та прилеглими кутами ∆DВС=∆D1В1С1.
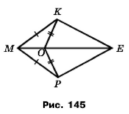
Задача 176. На рисунку 145 ∆МКО = ∆МРО. Доведіть, що ∆КОЕ = = ∆РОЕ.
Розв'язання.
Оскільки ∆МКО = ∆МРО, тому відповідні кути та сторони рівні КО = РО, ﮮ МОК = ﮮ МОР. Доведемо, що кути ﮮ КОЕ = ﮮ FOE, тобто різниця кутів дорівнює нулю. ﮮ KOE – ﮮ POE = (180˚ - ﮮ MOK) – (180˚ - ﮮ MOP) = ﮮ MOP – ﮮ MOK = 0˚. Сторона ОЕ спільна, за двома сторонами та кутом між ними ∆КОЕ = = ∆РОЕ.
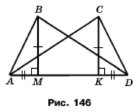
Задача 177. На рисунку 146 ВМ ﬩ АО, СК ﬩ АD, ВМ = СК, АМ = = КD. Доведіть, що ∆AВD = ∆СDA.
Розв'язання.
Розглянемо трикутники АМВ і CKD. За умовою сторони рівні ВМ = СК, АМ = КD, кути ﮮ AMB = ﮮ DKC = 90˚. За двома сторонами та кутом між ними ∆АМВ і ∆CKD. У рівних трикутників відповідні сторони та кути рівні АВ = CD, ﮮ ABD = ﮮ CDA. Розглянемо трикутники AВD і СDA. Сторона AD спільна, АВ = CD, ﮮ ABD = ﮮ CDA, за двома сторонами та кутом між ними ∆AВD = ∆СDA.
Задача 178. Доведіть, що бісектриси рівних трикутників, проведені з вершин відповідних кутів, рівні.
Розв'язання.
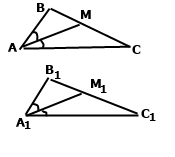
За умовою ∆АВС = ∆А1В1С1, у рівних трикутників рівні відповідні сторони та кути АС = А1С1, ﮮ АСВ = ﮮ А1С1В1, ﮮ ВАС = ﮮ В1А1С1, оскільки АМ бісектриса кута ВАС, А1М1 – бісектриса кута В1А1С1, ﮮ ВАС = 2 ﮮ МАС = ﮮ В1А1С1 = 2 ﮮ М1А1С1, кути рівні ﮮ МАС = ﮮ М1А1С1. За стороною АС = А1С1 та двома прилеглими кутами ﮮ МАС= ﮮ М1А1С1 і ﮮ МСА = ﮮ М1С1А1 маємо рівні трикутники ∆АМС = ∆А1М1С1. У рівних трикутників рівні відповідні сторони АМ = А1М1.
Задача 179. Доведіть, що в рівних трикутниках медіани, проведені до відповідних сторін, рівні.
Розв'язання.
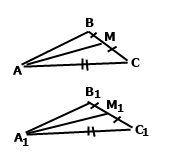
За умовою ∆АВС = ∆А1В1С1, у рівних трикутників рівні відповідні сторони та кути АС = А1С1, ﮮ АСВ = ﮮ А1С1В1, ВС = В1С1, оскільки АМ медіана до сторони ВС, А1М1 – медіана до сторони В1С1, ВС = 2МС = В1С1 = 2М1С1, відрізки рівні МС = М1С1. За двома сторонами АС = А1С1 і ВС = В1С1 та кутом між ними ﮮ МСА = ﮮ М1С1А1 маємо рівні трикутники ∆АМС = ∆А1М1С1. У рівних трикутників рівні відповідні сторони АМ = А1М1.
Задача 180. На продовженні медіани АМ трикутника АВС за точку М відкладено відрізок МК, який дорівнює АМ. Знайдіть відстань від точки К до вершини С, якщо АВ = 6 см.
Розв'язання.
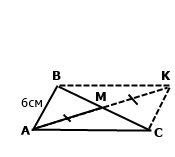
Розглянемо трикутники АВМ і КСМ. За умовою АМ = МК, АМ – медіана трикутника АВС, тому МВ = МС. Вертикальні кути рівні ﮮ ВМА = ﮮ СМК, тому за двома сторонами та кутом між ними трикутники рівні. У рівних трикутників рівні відповідні сторони КС = АВ = 6см.
Задача 181. Відрізки АВ і СD перетинаються в точці О та діляться точкою перетину навпіл. Доведіть, що ∆АВС = ∆ВАD.
Розв'язання.
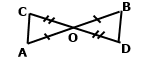
За умовою відрізки АВ і СD перетинаються в точці О та діляться точкою перетину навпіл, тобто AO = OB, CO = OD. Вертикальні кути рівні ﮮ COA = ﮮDOB. За двома сторонами та кутом між ними ∆АВС = ∆ВАD.
Задача 182. На рисунку 147 прямі m і n — серединні перпендикуляри сторін АВ і АС трикутника АВС. Доведіть, що точка О рівновіддалена від усіх вершин даного трикутника.
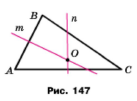
Розв'язання.
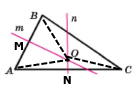
Розглянемо трикутники АОМ і ВОМ. Оскільки пряма m – серединний перпендикуляр, тоді АМ = ВМ, ﮮ АМО = ﮮ ВМО = 90˚. Сторона МО спільна. За двома сторонами та кутом між ними трикутники рівні ∆АОМ = ∆ВОМ. У рівних трикутників рівні відповідні сторони АО = ВО. Аналогічно можна довести, що трикутники рівні ∆AON = ∆CON, відповідно AO = CO, тобто точка О рівновіддалена від усіх вершин трикутника АВС.