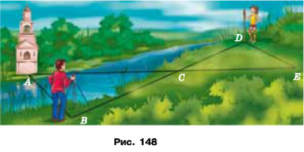
Задача 183. Для знаходження відстані від точки В до дзвіниці А, яка розташована на другому березі річки (рис. 148), за допомогою віх, рулетки й астролябії позначили на місцевості точки С, D і Е так, що В, С і D лежать на одній прямій, причому точка С є серединою відрізка ВD. Потім намітили пряму АЕ, яка проходить через точку С, причому ﮮAВС = ﮮСDЕ. Далі, вимірявши одну зі сторін трикутника СDЕ, визначили відстань від В до А. Яку сторону виміряли? Відповідь обґрунтуйте.

Розв'язання.

За умовою ВС = СD, ﮮAВС = ﮮСDЕ. Вертикальні кути рівні, тобто АСВ = ECD. За стороною та прилеглими кутами АВС = EDC. У рівних трикутників рівні відповідні сторони АВ = ED. Щоб знайти відстань до дзвіниці, виміряли сторону ED.

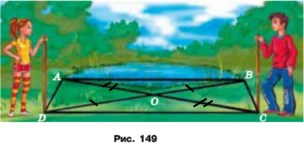
Задача 184. Для визначення ширини озера (рис. 149) на його березі позначили точки А і В, а потім ще точки С, D і О так, щоб точка О була спільною серединою відрізків АС і ВD. Як можна визначити ширину озера? Відповідь обґрунтуйте.

Розв'язання.

Розглянемо трикутники AOB і COD. За умовою точка О – спільна середина відрізків, тому АО = ОС, DO = OB. Вертикальні кути рівні, тому ﮮAOB = ﮮCOD. За двома сторонами та кутом між ними ∆AOB = ∆COD. У рівних трикутників відповідні сторони рівні AB = CD. Щоб визначити ширину озера треба виміряти довжину відрізка CD.

Задача 185.  Доведіть рівність двох трикутників за стороною, медіаною, проведеною до цієї сторони, та кутом між цією стороною та медіаною.

Розв'язання.

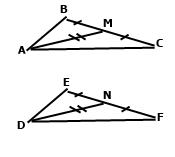
За умовою сторони рівні BC = EF, медіани рівні AM = DN, кути рівні ﮮAMC = ﮮDNF. Оскільки АМ і DN – медіани, тому BC = 2MC = EF = 2NF, MC = NF. Розглянемо трикутники AMC і DNF. За двома сторонами та кутом між ними вони рівні. Відповідні сторони рівні AC = DF, відповідні кути рівні ﮮАСМ = ﮮDFN. За умовою ВС = EF. Розглянемо трикутники ABC і DEF. За двома сторонами та кутом між ними трикутники рівні. 

Задача 186.  Доведіть рівність двох трикутників за стороною, прилеглим до неї кутом і бісектрисою трикутника, проведеною з вершини цього кута.

Розв'язання.

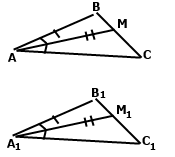
Розглянемо трикутники АВМ і А₁В₁М₁. За умовою АВ = А₁В₁, АМ = А₁М₁.  Оскільки АМ і А₁М₁ – бісектриси рівних кутів ВАС і В₁А₁С₁, тоді ﮮВАС = ﮮ2ВАМ = ﮮВ₁А₁С₁ = ﮮ2В₁А₁М₁, тобто ﮮВАМ = ﮮВ₁А₁М₁. За двома сторонами та кутом між ними ∆ВАМ = ∆В₁А₁М₁. У рівних трикутників відповідні сторони та кути рівні АВ = А₁В₁, ﮮВМА = ﮮВ₁М₁А₁. Розглянемо трикутники АМС і А₁М₁С₁. За умовою ﮮВАС = 2ﮮМАС = ﮮВ₁А₁С₁ = 2ﮮМ₁А₁С₁, тобто ﮮМАС = ﮮМ₁А₁С₁, переконаємось, що ﮮАМС = ﮮА₁М₁С₁, тобто різниця величин двох кутів дорівнює нулю. Кути розгорнуті ﮮВАС = ﮮВ₁М₁С₁ = 180˚. Тому ﮮАМС – ﮮА₁М₁С₁ = (180˚ - ﮮВМА) – (180˚ - ﮮВ₁М₁А₁) = ﮮВ₁М₁А₁ – ﮮВМА = 0˚. За стороною і двома прилеглими кутами ∆АМС = ∆А₁М₁С₁. У рівних трикутників відповідні сторони АС = А₁С₁. Розглянемо трикутники АВС = А₁В₁С₁, За двома сторонами АВ = А₁В₁, АС = А₁С₁ та кутом між ними ﮮВАС = ﮮВ₁А₁С₁ трикутники рівні.

Задача 187.  Доведіть рівність двох трикутників за бісектрисою, кутом, з вершини якого проведено цю бісектрису, і кутом, що утворює бісектриса зі стороною, до якої її проведено.

Розв'язання.

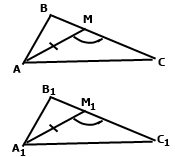
Розглянемо трикутники АВМ і А₁В₁М₁. За умовою АВ = А1В1, АМ = А₁М₁, ﮮВАС = ﮮВ₁А₁С₁. Оскільки АМ і А₁М₁ – бісектриси рівних кутів ВАС і В₁А₁С₁, тоді ﮮВАС = 2ﮮВАМ = ﮮВ₁А₁С₁ = 2ﮮВ₁А₁М₁, тобто ﮮВАМ = ﮮВ₁А₁М₁. За двома сторонами та кутом між ними ∆ВАМ = ∆В₁А₁М₁. У рівних трикутників відповідні сторони та кути рівні АВ = А₁В₁, ﮮВМА = ﮮВ₁М₁А₁. Розглянемо трикутники АМС і А₁М₁С₁. За умовою ﮮВАС = 2ﮮМАС = ﮮВ₁А₁С₁ = 2ﮮМ₁А₁С₁, тобто ﮮМАС = ﮮМ₁А₁С₁, переконаємось, що ﮮАМС = ﮮА₁М₁С₁, тобто різниця величин двох кутів дорівнює нулю. Кути розгорнуті ﮮВАС = ﮮВ₁М₁С₁ = 180˚. Тому ﮮАМС – ﮮА₁М₁С₁ = (180˚ - ﮮВМА) – (180˚ - ﮮВ₁М₁А₁) = ﮮВ₁М₁А₁ – ﮮВМА = 0˚. За стороною і двома прилеглими кутами ∆АМС = ∆А₁М₁С₁. У рівних трикутників відповідні сторони і кути рівні АС = А₁С₁, ﮮАСВ = ﮮА₁С₁В₁, МС = МС₁. За основною властивістю довжини відрізка ВС = ВМ + МВ = В₁С₁ = В₁М₁ + М₁С₁. Трикутники АВС і А₁В₁С₁ рівні.

Задача 188.  Серединний перпендикуляр сторони ВС трикутника АВС перетинає сторону AВ у точці D. Знайдіть відрізок AD, якщо СD = 4 см, AВ = 7 см.

Розв'язання.

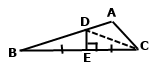
Розглянемо трикутники BDE і CDE. За умовою DE – серединний перпендикуляр сторони ВС, тобто ВЕ = ЕС і BED = CED = 90˚. Сторона DE спільна, тому ∆BDE і ∆CDE. У рівних трикутників відповідні сторони рівні, тобто BD = DC = 4см. За основною властивістю довжини відрізка AB = AD + DB, AD = AB – DB = 7см – 3см = 4см.

Задача 189.  Серединний перпендикуляр сторони AВ трикутника AВС перетинає сторону ВС у точці М. Знайдіть довжину сторони AС трикутника AВС, якщо ВС = 16 см, а периметр трикутника АMС дорівнює 26 см.

Розв'язання.

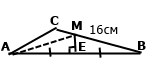
Розглянемо трикутники АМЕ і ВМЕ. Оскільки ЕМ – серединний перпендикуляр сторони АВ, тоді АЕ = ЕВ, ﮮАЕМ = ﮮВЕМ = 90˚. Сторона МЕ спільна для двох трикутників. За двома сторонами та кутом між ними  ∆АМЕ = ∆ВМЕ. У рівних трикутників рівні відповідні сторони АМ = ВМ. За основною властивістю довжини відрізка ВС = ВМ + МС, оскільки АМ = ВМ маємо ВС = МА + МС = 16см. За умовою АС + МА + МС = 26см, тоді АС = 26см – (МА + МС) = 26см – 16см = 10см.

Задача 190.  На рисунку 150 ОA = ОD. Додайте ще одну умову таку, щоб трикутники AОС і DOВ виявилися рівними:

1)  за першою ознакою рівності трикутників;

2)  за другою ознакою рівності трикутників.

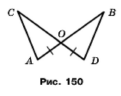
Розв'язання.

1) ознака рівності трикутників за двома сторонами і кутом між ними.

СО = ОВ (оскільки кути вертикальні рівні).

2) ознака рівності трикутників за стороною та прилеглими кутами.

САО = BDO (оскільки кути вертикальні рівні).

Задача 191.  Відрізки AВ і СD перетинаються в точці О та діляться цією точкою навпіл. На відрізку AС позначено точку М, а на відрізку ВD — точку К так, що АМ = ВК. Доведіть, що: 1) ОМ = ОК; 2) точки М, О і К лежать на одній прямій.

Розв'язання.

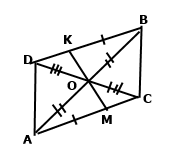
1) Розглянемо трикутники AOC і BOD, за умовою відрізки AВ і СD перетинаються в точці О та діляться цією точкою навпіл, тобто OA = OB, OD = OC. Вертикальні кути рівні ﮮBOD = ﮮAOC. За двома сторонами та кутом між ними трикутники рівні. У рівних трикутників рівні відповідні кути ﮮOAM = ﮮOBK, AC = BD, ﮮOCA = ﮮBDO. Розглянемо трикутники АОМ і ВОК. За умовою АМ = ВК. За двома сторонами АМ = ВК, OA = OB та кутом між ними ﮮOAM = ﮮOBK трикутники рівні. У рівних трикутників рівні відповідні сторони ОМ = ОК.

2) Оскільки ОМ = ОК, треба довести, що кут КОМ є розгорнутим. Розглянемо рівні трикутники ОАМ і ОВК, у них рівні відповідні кути ﮮКОМ = ﮮМОА. Також рівні вертикальні кути ﮮВОС = ﮮАОD, утворені при перетині відрізків АВ і СD. Розглянемо трикутники COM і DOK. У них ﮮOCA = ﮮBDO. Оскільки за умовою АМ = ВК, а AC = BD, з основної властивості довжини відрізка випливає, що AC = AM + MC = BD = BK + KD, тобто МС = KD, трикутники за двома сторонами та кутом між ними рівні, таким чином ﮮCOM = ﮮDOK. За основною властивістю величини кута маємо ﮮKOB + ﮮBOC + ﮮCOM + ﮮCOM + ﮮMOA + ﮮAOD + ﮮDOK = 360°, 2(ﮮKOB + ﮮBOC + ﮮCOM) = 360°, ﮮKOB + ﮮBOC + ﮮCOM = 180°. Відрізки ОК і ОМ мають спільний початок та утворюють розгорнутий кут, значить точки К,О,М лежать на одній прямій.

Задача 192.  На одній стороні кута з вершиною в точці О (рис. 151) позначено точки А і В, а на другій — точки С і D так, що ОА = ОС, АВ = СD. Доведіть, що промінь ОМ є бісектрисою кута ВОD, де М — точка перетину відрізків AО і ВС.

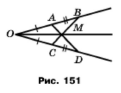
Розв'язання.

Треба довести, що ﮮВОМ = ﮮDOM. Розглянемо трикутники AOD і COB. За умовою АВ = СD, сторона ОМ спільна, кут ВОD спільний, за двома сторонами та кутом між ними трикутники рівні. У рівних трикутників відповідні сторони та кути рівні ВC = AD, ﮮCBO = ﮮADO, ﮮOAD = ﮮOCB. Розглянемо трикутники АМВ і CMD. Кути ОАВ і OCD розгорнуті. Доведемо, що кути ВАМ і МСD рівні, тобто різниця величин кутів дорівнює 0°. За основною властивістю величини кута маємо  ﮮОАВ = ﮮОАМ + ﮮМАВ, ﮮOCD = ﮮOCM + ﮮMCD. Тоді ﮮMAB – ﮮMCD = (ﮮOAB – ﮮОАМ) – (ﮮOCD – ﮮOCМ) = (180° - ﮮOAM) – (180° - ﮮOСM) = ﮮOCМ – ﮮOAM = 0°. За стороною та прилеглими кутами ΔАМВ = ΔCMD. У рівних трикутників відповідні сторони рівні АМ = МС. Розглянемо трикутники АОМ і СОМ. За двома сторонами ОА = ОС, АМ = МС та кутом між ними  ﮮOAD = ﮮOCB маємо рівні трикутники  ΔАОМ = ΔСОМ. У рівних трикутників відповідні кути рівні ﮮАОМ = ﮮСОМ = ﮮВОМ = ﮮDOM. За основною властивістю величини кута ﮮАОС = ﮮАОМ + ﮮМОС = 2ﮮАОМ. Промінь ОМ ділить кут АОС на два рівні кути, тому він є бісектрисою кута.

Задача 193.  Чи є правильним твердження: якщо через кожні дві з трьох даних точок провести пряму, то одержимо три прямі?

Розв'язання.

За основною властивістю прямої через дві точки можна провести однозначно пряму. Таких пар точок буде 3, тому одержимо три прямі.

Задача 194.  Промені ОD і ОF — бісектриси суміжних кутів АОВ і ВОС відповідно, ﮮAОD: ﮮFОС = 2:1. Знайдіть кути АОD і FОС.

Розв'язання.

Оскільки кути суміжні, то АОВ + ВОС = 180°. Оскільки OD і ОF — бісектриси суміжних кутів АОВ і ВОС відповідно, АОВ = 2AOD, BOC = 2FOC. 2AOD + 2FOC = 180°. AOD + FOC = 90°.

2 + 1 = 3 (ч.) – частини припадає на суму кутів AOD + FOC.

90 : 3 = 30 (°) – градусів припадає на одну частину.

30 • 2 = 60 (°) – градусів дорівнює кут AОD.

30 • 1 = 30 (°) – градусів дорівнює кут FОС.

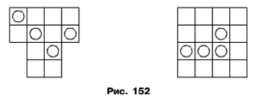
Задача 195. Розділіть кожну з фігур, що зображено на рисунку 152, уздовж ліній сітки на чотири рівні частини так, щоб у кожній частині було тільки одне коло.