Задача 196.  Накресліть:

1)  різносторонній гострокутний трикутник;

2)  рівнобедрений прямокутний трикутник;

3)  рівнобедрений тупокутний трикутник.

Розв'язання.

Задача 197.  Накресліть:

1)  різносторонній прямокутний трикутник;

2)  різносторонній тупокутний трикутник.

Розв'язання.

Задача 198.  Накресліть рівнобедрений трикутник з бічною стороною завдовжки 3 см так, щоб його кут при вершині був: 1) гострим; 2) прямим; 3) тупим. У побудованих трикутниках проведіть висоти до бічних сторін.

Розв'язання.

Задача 199. 1) Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює 13 см, а бічна сторона — 8 см. 2) Периметр рівнобедреного трикутника дорівнює 39 см, а основа — 15 см. Знайдіть бічні сторони трикутника.

Розв'язання.

1) Оскільки периметр трикутника – сума довжин сторін трикутника, а в рівнобедреному трикутнику бічні сторони рівні, маємо Р = 13см + 8см + 8см = 29см.

2) Периметр трикутника – сума довжин сторін трикутника. У рівнобедреному трикутнику бічні сторони рівні, маємо бічна сторона а = (39см - 15см) : 2 = 12см. 

Задача 200.  Периметр рівнобедреного трикутника дорівнює 28 см, а бічна сторона — 10 см. Знайдіть основу трикутника.

Розв'язання.

Периметр трикутника – сума довжин сторін трикутника. У рівнобедреному трикутнику бічні сторони рівні, маємо основа с = (28см – 2 • 10см) = 8 см. 

Задача 201.  Знайдіть сторони рівнобедреного трикутника, периметр якого дорівнює 32 см, а основа на 5 см більша за бічну сторону.

Розв'язання.

Нехай х – довжина бічної сторони рівнобедреного трикутника, тоді х + 5 – довжина основи трикутника. Периметр трикутника – сума довжин сторін трикутника. У рівнобедреному трикутнику бічні сторони рівні, складемо рівняння

х + х + (х + 5) = 32

3х + 5 = 32

3х = 32 – 5 

3х = 27

х = 27 : 3 

х = 9

Бічні сторони рівнобедреного трикутника дорівнюють по 9 см, основа дорівнює 9 + 5 = 14 см.

Задача 202.  Знайдіть сторони рівнобедреного трикутника, периметр якого дорівнює 54 см, а основа в 4 рази менша від бічної сторони.

Розв'язання.

Нехай х – довжина основи рівнобедреного трикутника, тоді 4х  – довжина бічної сторони трикутника. Периметр трикутника – сума довжин сторін трикутника. У рівнобедреному трикутнику бічні сторони рівні, складемо рівняння

4х + 4х + х = 54

9х = 54

х = 54 : 9 

х = 6

Основа рівнобедреного трикутника дорівнює 6 см, бічні сторони дорівнюють по 6 • 4 = 24 см.

Задача 203.  У рівнобедреному трикутнику АВС сторона АС — основа, ﮮВСА = 40˚, ﮮАВС = 100˚, ВD — медіана. Знайдіть кути трикутника АВD.

Розв'язання.

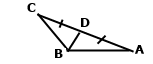
У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. Оскільки BD – висота, то маємо ﮮCDB = ﮮADB = 90˚. Оскільки BD бісектриса, то маємо ﮮABD = ½ ﮮBCA = ½ 100˚ = 50˚. Оскільки BD – медіана, то маємо DC = DA. Розглянемо трикутники BDC і BDA. За двома сторонами DC = DA, BD – спільна та кутом між ними ﮮCDB = ﮮADB трикутники BDC і BDA рівні.  У рівних трикутників відповідні кути рівні ﮮВАD = ﮮBCD = ﮮBCA = 40˚.

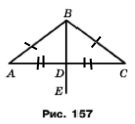
Задача 204.  На рисунку 157 АВ = ВС, ВD — медіана трикутника АВС, ﮮАВD = 53°. Знайдіть кути АВС і АDЕ.

Розв'язання.

Оскільки АВ = ВС, то трикутник АВС рівнобедрений. За умовою BD – медіана трикутника. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. З означення бісектриси слідує ﮮABC = 2 ﮮABD = 2 • 53˚ = 106˚ . З означення висоти  слідує ﮮADE = 90˚.

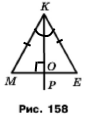
Задача 205.  На рисунку 158 МК = КЕ, ОЕ= 6 см, ﮮМКЕ = 48°, ﮮРОЕ = 90°. Знайдіть сторону МЕ і кут МКО.

Розв'язання.

Оскільки АВ = ВС, то трикутник АВС рівнобедрений. За умовою  ﮮРОЕ = 90°, тобто КО -  висота трикутника, проведена до основи. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. З означення бісектриси слідує ﮮМКЕ = 2ﮮМКО, ﮮМКО = ﮮМКЕ : 2 = 48˚ : 2 = 24˚ . З означення медіани слідує МЕ = 2ОЕ = 6см • 2 = 12см .

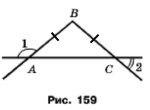
Задача 206. На рисунку 159 AВ = ВС, ﮮ1 = 140°. Знайдіть кут 2.

Розв'язання.

За основною властивістю величини кута маємо ﮮ1 + ﮮВАС = 180˚, ﮮВАС = 180˚ - 140˚ = 40˚. За умовою  AВ = ВС, тому трикутник АВС рівнобедрений. У рівнобедреного трикутника кути при основі рівні ﮮВАС = ﮮВСА. В свою чергу вертикальні кути рівні  ﮮ2 = ﮮВСА, тобто ﮮ2 = ﮮВСА = ﮮВАС = 40˚.

Задача 207.  Кут, вертикальний до кута при вершині рівнобедреного трикутника, дорівнює 68˚. Знайдіть кут між бічною стороною трикутника та медіаною, проведеною до основи.

Розв'язання.

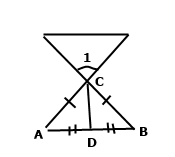
Вертикальні кути рівні ﮮ 1 = ﮮ АСВ = 68˚. За умовою трикутник АВС рівнобедрений. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. З означення бісектриси маємо ﮮ АСB = 2 ﮮ ACD, тому ﮮ ACD = ﮮ ACB : 2 = 68˚ : 2 = 34˚

Задача 208.  Кут, суміжний із кутом при вершині рівнобедреного трикутника, дорівнює 76˚. Знайдіть кут між бічною стороною трикутника та висотою, опущеною на основу.

Розв'язання.

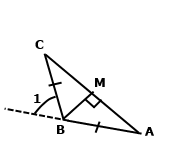
У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. З означення бісектриси маємо ﮮ СВА = 2 ﮮ СВМ. За основною властивістю величини кута 180˚ = ﮮ 1 + ﮮ СВА, 180˚ = ﮮ 1 + 2 ﮮ СВМ, ﮮ СВМ = (180˚ – 76˚) : 2 =  52˚

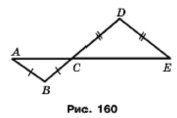
Задача 209.  На рисунку 160 АВ = ВС, ВС = DЕ. Доведіть, що ﮮА = ﮮЕ.

Розв'язання.

За умовою АВ = ВС, тоді трикутник АВС – рівнобедрений, у рівнобедреного трикутника кути при основі рівні ﮮ А = ﮮ АСВ. Також ВС = DЕ, тоді трикутник СDЕ – рівнобедрений, кути при основі рівні ﮮ ECD = ﮮ Е. Кути АСВ та ECD – вертикальні, значить рівні. Маємо ﮮ АСВ = ﮮ ЕCD = ﮮ A = ﮮ E, ﮮA = ﮮ E.

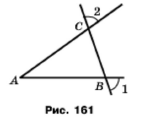
Задача 210.  Пряма перетинає сторони кута А в точках В і С так, що АВ = АС (рис. 161). Доведіть, що ﮮ1 = ﮮ2.

Розв'язання.

За умовою АВ = АС, тому трикутник АВС рівнобедрений. У такому трикутнику кути при основі рівні ﮮ АСВ = ﮮ АВС. Вертикальні кути рівні ﮮ АСВ = ﮮ 2, ﮮ АВС = ﮮ 1, тобто ﮮ АСВ = ﮮ 2 = ﮮ АВС = ﮮ 1. Кути рівні ﮮ 1 = ﮮ 2.