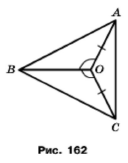
Задача 211.  На рисунку 162 АО=СО, ﮮAОВ = ﮮСОВ. Доведіть, що трикутник АВС рівнобедрений.

Розв'язання.

Розглянемо трикутники АВО і СОВ. За умовою АО=СО, ﮮAОВ = ﮮСОВ, а сторона ОВ – спільна. Тому за двома сторонами та кутом між ними трикутники рівні. У рівних трикутників рівні відповідні сторони. Маємо ВА = ВС. Такий трикутник АСВ за означенням рівнобедрений.

Задача 212.  Трикутник АВС — рівнобедрений з основою АС, ВD — його бісектриса, DМ — бісектриса трикутника ВDС. Знайдіть кут ADМ.

Розв'язання.

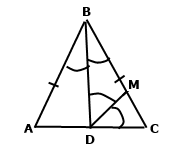
За умовою трикутник АВС — рівнобедрений з основою АС. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. З означення висоти маємо ADB = CDB = 90˚. З означення бісектриси маємо BDM = ½ CDB = ½ 90˚ = 45˚. За основною властивістю величини кута ADM = ADB + BDM = 90˚ + 45˚ = 135˚.

Задача 213.  Один учень стверджує, що деякий трикутник рівнобедрений, а другий учень — що цей трикутник рівносторонній.

1)  Чи можуть обидва учні бути правими?

2)  У якому випадку правий тільки один учень і який саме?

Розв'язання.

1) Так, якщо трикутник рівносторонній, то він є рівнобедреним.

2) Якщо у рівнобедреного трикутника довжини бічної сторони та основи різні, тоді неправий учень, що стверджує про рівносторонній трикутник. 

Задача 214.  Використовуючи ознаки рівності трикутників, доведіть ознаку рівності рівнобедрених трикутників за бічною стороною та кутом при вершині.

Розв'язання.

Якщо трикутник рівнобедрений, тоді його дві бічні сторони рівні. Кут при вершині буде кутом між бічними сторонами. Використаємо ознаку рівності трикутників за двома сторонами та кутом між ними. Тому, якщо за бічною стороною та кутом при вершині рівнобедрені трикутники рівні. 

Задача 215.  Використовуючи ознаки рівності трикутників, доведіть ознаку рівності рівнобедрених трикутників за основою та прилеглим до неї кутом.

Розв'язання.

Якщо трикутник рівнобедрений, тоді його прилеглі кути при основі рівні. Використаємо ознаку рівності трикутників за стороною та прилеглими кутами. Тому, якщо за основою та прилеглим до неї кутом рівнобедрені трикутники рівні. 

Задача 216.  На основі АС рівнобедреного трикутника АВС позначено точки М і К так, що точка М лежить між точками А і К, причому АМ = СК. Доведіть, що трикутник МВК рівнобедрений.

Розв'язання.

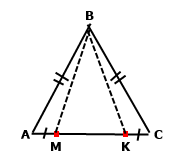
За умовою трикутник АВС рівнобедрений, тоді АВ = АС, кути при основі рівні А = С. Розглянемо трикутники АВМ і СВК. За умовою АМ = СК, тому за двома сторонами та кутом між ними ∆АВМ = ∆СВК. У рівних трикутників рівні відповідні сторони, отже, МВ = КВ. За означенням трикутник МВК – рівнобедрений. 

Задача 217.  У трикутнику МКЕ відомо, що МК = МЕ. На стороні КЕ позначено точки F і N так, що точка N лежить між точками F і Е, причому ﮮКМF = ﮮЕМN. Доведіть, що ﮮМFN = ﮮМNF.

Розв'язання.

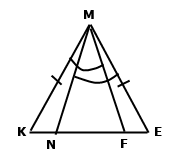
За умовою МК = МЕ, тому трикутник МКЕ рівнобедрений, а також ﮮКМF = ﮮЕМN. У рівнобедреному трикутнику кути при основі рівні MKE = MEK. За стороною  і прилеглими кутами ∆КМF = ∆EMN. У рівних трикутників рівні відповідні кути ﮮМFN = ﮮМNF.

Задача 218.  На бічних сторонах СA і СВ рівнобедреного трикутника AВС відкладено відповідно рівні відрізки СК і СМ. Доведіть, що: 1) ∆АМС = ∆ВКС; 2) ∆AМВ = ∆ВКA.

Розв'язання.

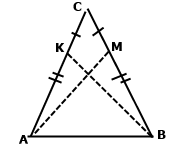
1) За умовою СК = СМ, трикутник АВС рівнобедрений з бічними сторонами СA і СВ , тому СA=СВ.  Розглянемо трикутники АМС і ВКС. За двома сторонами СA=СВ і СК = СМ та спільним кутом між ними ﮮАСВ трикутники рівні, тобто ∆АМС = ∆ВКС.

2) За умовою СК = СМ . Також трикутник АВС рівнобедрений з бічними сторонами СA і СВ , тому СA=СВ. У рівнобедреного трикутника кути при основі рівні ﮮКАВ = ﮮМАВ. За основною рівністю довжини відрізка маємо СВ = СМ + МВ, СА = СК + КА. Доведемо що відрізки МВ і КА рівні, різниця довжин дорівнює нулю. МВ – КА = (СВ – СМ)  – (СА – СК) = СВ – СА + СК + СМ = 0˚. Розглянемо трикутники АМС і ВКС. За двома сторонами МВ = КА , сторона АВ – спільна, та кутом між ними  ﮮКАВ = ﮮМАВ трикутники рівні, тобто ∆AМВ = ∆ВКA.

Задача 219.  У рівнобедреному трикутнику AВС з основою АС на медіані ВD позначили довільну точку М. Доведіть, що: 1) ∆АМВ = ∆СМВ; 2) ∆АМD = ∆СМD.

Розв'язання.

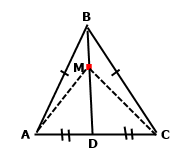
1) За умовою трикутник АВС рівнобедрений з основою АС, тому АВ = СВ. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. Розглянемо трикутники АМВ і СМВ. За означенням бісектриси BD маємо ﮮAВМ = ﮮCВМ. Сторона ВМ спільна. За двома сторонами та кутом між ними трикутники рівні ∆АМВ = ∆СМВ.

2) За умовою трикутник АВС рівнобедрений з основою АС, тому АВ = СВ. У рівнобедреному трикутнику АВС бісектриса, медіана та висота, проведені до його основи збігаються. Розглянемо трикутники АМD і СМD. За означенням медіани BD маємо AD = CD. За означенням висоти BD маємо ﮮBDA = ﮮBDC = 90˚. Сторона MD спільна. За двома сторонами та кутом між ними трикутники рівні ∆АМD = ∆СМD.

Задача 220. Доведіть, що бісектриси рівнобедреного трикутника, проведені з вершин кутів при основі, рівні. 

Розв'язання.

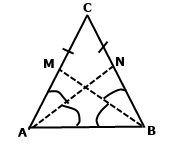
За умовою трикутник АВС – рівнобедрений з основою АВ, тоді бічні сторони рівні АС = ВС, кути при основі рівні ﮮСАВ = ﮮСВА. За означенням бісектриси АN маємо ﮮСАВ = 2ﮮСАN. За означенням бісектриси ВМ маємо ﮮСВА = 2ﮮСВМ. Покажемо, що  кути САN і СВМ рівні, різниця їхніх величин дорівнює нулю.  ﮮСАN – ﮮСВМ = (ﮮСАВ – ﮮСВА) : 2 = 0˚. Розглянемо трикутники AСN і BCM. За стороною АС = ВС та прилеглими кутами ﮮСАN = ﮮСВМ, кут АСВ спільний трикутники рівні ∆САN = ∆СВМ. У рівних трикутників рівні відповідні сторони АN = BM. А вони є шуканими бісектрисами рівнобедреного трикутника, проведені з вершин кутів при основі.

Задача 221. Доведіть, що медіани рівнобедреного трикутника, проведені до бічних сторін, рівні.

Розв'язання.

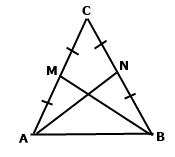
За умовою трикутник АВС – рівнобедрений з основою АВ, тоді бічні сторони рівні АС = ВС, кути при основі рівні ﮮСАВ = ﮮСВА. За означенням медіани АN маємо ВС = 2ВN. За означенням медіани ВМ маємо АC = 2AM. Покажемо, що  відрізки АM і ВN рівні, різниця їхніх величин дорівнює нулю.  АМ – ВN = (АC – BC) : 2 = 0. Розглянемо трикутники ABM і BAN. За двома сторонами АM = ВN, АВ – спільна сторона та кутом між ними ﮮСАВ = ﮮСВА трикутники рівні ∆ВАN = ∆АВМ. У рівних трикутників рівні відповідні сторони АN = BM. А вони є медіанами рівнобедреного трикутника, проведеними до бічних сторін.

Задача 222.  Доведіть, що середини сторін рівнобедреного трикутника є вершинами рівнобедреного трикутника.

Розв'язання.

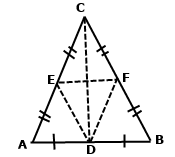
За умовою трикутник АВС рівнобедрений з основою АВ, тому бічні сторони рівні АС = ВС, кути при основі рівні ﮮEAD = ﮮFBD. Точка D – середина сторони АВ, точка Е – середина відрізка АС, точка F – середина відрізка СВ. За основною властивістю довжини відрізка маємо відповідно АС = 2АЕ, АВ = 2АD = 2DB, ВС = 2BF. Доведемо, що відрізки АЕ і BF рівні, переконаємось, що різниця цих величин дорівнює нулю. Справді АЕ – BF = ½ AC – ½ BC = ½ (AC – BC) = 0. Розглянемо трикутники ADE і BDF. За двома сторонами AE = BF, AD = DB та кутом між ними ﮮEAD = ﮮFBD трикутники рівні ∆ADE = ∆BDF. У рівних трикутників рівні відповідні сторони DE = DF. Трикутник EDF рівнобедрений, а середини сторін рівнобедреного трикутника АВС є його вершинами

Задача 223.  Знайдіть третю сторону рівнобедреного трикутника, якщо дві інші його сторони дорівнюють 7 см і 4 см. Скільки розв'язків має задача?

Розв'язання.

Задача має два розв'язки. У рівнобедреного трикутника бічні сторони рівні.

1) Нехай бічна сторона трикутника дорівнює 7см, основа 4 см. Тоді третя сторона дорівнює бічній стороні 7см.

1) Нехай бічна сторона трикутника дорівнює 4см, основа 7 см. Тоді третя сторона дорівнює бічній стороні 4см.

Задача 224.  Одна зі сторін рівнобедреного трикутника дорівнює 4 см. Знайдіть дві інші сторони, якщо периметр трикутника дорівнює 14 см.

Розв'язання.

Задача має два розв'язки.

1) Нехай бічна сторона дорівнює 4см, у рівнобедреного трикутника бічні сторони рівні, тому друга сторона дорівнює 4см. Знайдемо довжину основи: 14см – 4см • 2 = 2см. 

2) Нехай основа дорівнює 4см. У рівнобедреного трикутника бічні сторони рівні. Знайдемо довжину бічної сторони: (14см – 4см) : 2 = 5см. 

Задача 225.  Чи є правильним твердження:

1)  бісектриса рівнобедреного трикутника є його висотою та медіаною;

2)  бісектриса рівностороннього трикутника є його висотою та медіаною;

3)  якщо периметр трикутника в 3 рази більший за одну з його сторін, то цей трикутник рівносторонній?

Розв'язання.

1) так.

2) так.

3) ні (периметр трикутника 3см + 2см + 4см = 9см у 3 рази більший за одну з його сторін, але довжини сторін різні).

Задача 226.  На сторонах рівностороннього трикутника АВС (рис. 163) позначили точки М, К і D так, що AD = ВМ = СК. Доведіть, що трикутник МКD рівносторонній.

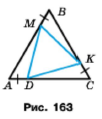
Розв'язання.

За умовою AD = ВМ = СК , трикутник АВС рівносторонній, тоді АС = ВС = АB, А = В = С. Доведемо, що AM = DC, тобто різниця довжин відрізків дорівнює нулю. За основною властивістю довжини відрізка AB = AM + BM, AC = AD + DC. Тоді DC – AM = (AC - AD) – (AB - BM) = AC – AB + BM – AD = 0. 

Задача 227.  На продовженнях сторін AВ, ВС, АС рівностороннього трикутника AВС (рис. 164) за точки А, B і C відповідно відклали рівні відрізки AD, ВК і СЕ. Доведіть, що трикутник DЕК рівносторонній. 

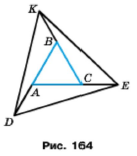
Розв'язання.

Треба довести, що КЕ = ED = DК. За умовою AD = ВК = СЕ, трикутник АВС рівносторонній, тому АС = ВС = ВА, ВАС = АСB = ВAС. Розглянемо трикутники КСЕ, ЕАD. За основною властивістю величини кута ﮮАСЕ = ﮮАСВ + ﮮВСЕ, ﮮDAB = ﮮDAC + ﮮBAC. Доведемо, що кути ВСЕ і СAD, тобто різниця дорівнює нулю. ﮮВСЕ – ﮮDAC = (ﮮACE – ﮮACB) – (ﮮDAB – ﮮBAC) = 180° -  ﮮACB - 180° + ﮮACB = 0°. За основною властивістю довжини відрізка КС = ВK + ВС, BD = AD + BA, значить КС = BD. За двома сторонами та кутом між ними трикутники рівні. У рівних трикутників рівні відповідні сторони KE = ED. Аналогічно доводиться рівність інших сторін ED і DK .

Задача 228. Основа рівнобедреного трикутника дорівнює 20 см, а його медіана ділить даний трикутник на два трикутники так, що периметр одного з них на 6 см менший від периметра другого. Знайдіть бічну сторону даного трикутника. Скільки розв'язків має задача?

Розв'язання.

Задача 229.  На рисунку 165 а ﬩ b, перший кут дорівнює 35 . Знайдіть кути 2, 3, 4.

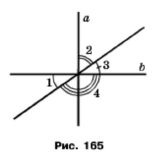
Розв'язання.

Вертикальні кути перший і третій рівні, третій кут дорівнює 35˚. Оскільки за умовою а ﬩ b, тому четвертий кут дорівнює 90˚, за основною властивістю величини кута сума третього і другого кута дорівнює 90˚. Тому другий кут дорівнює 55˚.

Задача 230.  Точки С і D поділили відрізок АВ, довжина якого дорівнює а, на три відрізки АС, СD і DВ так, що АС = 2СD, СD = 2DВ. Знайдіть відстань між: 1) точкою А та серединою відрізка СD; 2) серединами відрізків АС і DВ.

Розв'язання.

1) За умовою АС = 2СD, СD = 2DВ

Задача 231. Нарисуйте шестикутник, який можна одним розрізом поділити на два трикутники.