Завдання 826. Узимку вівці на день дають 2 кг силосу. Скільки потрібно силосу шести вівцям на тиждень?
Розв’язання:
1 спосіб.
2 • 7 = 14 (кг) - потрібно силосу одній вівці на тиждень.
14 • 6 = 84 (кг) - потрібно силосу шести таким вівцям.
2 спосіб.
2 • 6 = 12 (кг) - потрібно силосу шести вівцям на один день.
12 • 7 = 84 (кг) - потрібно силосу шести вівцям на 7 днів.
3 спосіб.
2 • 6 • 7 = 2 • 7 • 6 = 84 (кг) - потрібно силосу шести вівцям на 7 днів.
Відповідь: 84 кілограмів.
Завдання 827. Для ремонту двох під'їздів витратили 17 банок фарби, по 4 кг у кожній. На перший під'їзд витратили 6 банок фарби. Скільки кілограмів фарби пішло для ремонту другого під'їзду? (Розв'яжи задачу двома способами.)
Розв’язання:
1 спосіб. Вираз Вираз (4 • 17) – (4 • 6)
4 • 17 = 68 (кг) - витратили фарби для ремонту двох під'їздів.
4 • 6 = 24 (кг) - витратили фарби для ремонту першого під'їзду.
68 – 24 = 44 (кг) - витратили фарби для ремонту другого під'їзду.
2 спосіб. Вираз 4 • (17 – 6)
17 – 6 = 11 (б.) - витратили банок фарби для ремонту другого під'їзду.
4 • 11 = 44 (кг) - витратили кілограмів фарби для ремонту другого під'їзду.
Відповідь: 44 кілограми.
Завдання 828. Знайди значення виразів, якщо а = 24.
3 • а (60 - а) : 4 60 - а : 4
Розв’язання:
3 • 24 = 24 • 3 = (20 • 3) + (4 • 3) = 60 + 12 = 72
(60 – 24) : 4 = 36 : 4 = 9
60 – 24 : 4 = 60 – 6 = 54
Завдання 829. Учень побудував пряму і послідовно відклав на ній відрізки, які є сторонами прямокутника ABCD. Виміряй довжину утвореного відрізка.
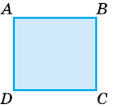
Відповідь: АВ + ВС + СD + DА = 4 • АВ
Завдання 830. Побудуй пряму й послідовно відклади на ній відрізки, які є сторонами прямокутника КМОР.

Знайди периметр прямокутника.
Розв’язання:
Р = 30 мм + 13 мм + 30 мм + 13 мм = 86 мм
Запиши рівність для обчислення периметра прямокутника з довжиною а і шириною b.
Розв’язання:
Р = (a + b) • 2
Р = 2 • а + 2 • b
Завдання 831*. Івась почав читати книжку, коли Маринка вже прочитала 18 сторінок тієї самої книжки. Чи наздожене Івась Маринку за 5 днів, якщо читатиме щодня по 11 сторінок, а Маринка — по 7 сторінок?
Розв’язання:
11 • 5 = 55 (с.) - сторінок прочитає Івась.
7 • 5 + 18 = 53 (с.) - до того часу прочитає Маринка.
Відповідь: так, наздожене.
Завдання 832°. Склади задачу за коротким записом і розв'яжи її.
У десяти мішках було 500 кг картоплі. Скільки кілограмів картоплі буде у 12 таких мішках?
10 мішків — 500 кг
12 мішків — ?
Розв’язання:
500 : 10 = 50 (кг) - кілограмів картоплі було в одному мішку.
50 • 12 = 600 (кг.) - буде кілограмів картоплі.
Відповідь: 600 кілограмів.
Завдання 833°.
5 • 25 + 3 = 25 • 5 + 3 = (20 • 5) + (5 • 5) + 3 = 100 + 25 + 3 = 128
3 • 33 – 1 = (33 • 3 ) -1 = (30 • 3) + (3 • 3) - 1 = 90 + 9 - 1 = 98
2 • 13 • 3 = 13 • (2 • 3) = 13 • 6 = (10 • 6) + (3 • 6) = 60 + 18 = 78
3 • 18 : 9 = (18 : 9) • 3 = 2 • 3 = 6
(70 – 10) : 20 = 60 : 20 = 3
70 – 10 : 2 = 70 – 5 = 65
7 • 13 + 9 = 13 • 7 + 9 = (10 • 7) + (3 • 7) + 9 = 70 + (21 + 9) = 100
13 • 7 – 9 = (10 • 7) + (3 • 7) – 9 = 70 + 21 – 9 = 82
Завдання 834. 1) Розглянь записи і прочитай пояснення.
3 • 24 = □
3 • 20 = 60
3 • 4 = 12
60 + 12 = 72
При множенні одноцифрового числа на двоцифрове можна спочатку двоцифрове число розкласти на розрядні доданки, а потім одноцифрове число помножити окремо на доданки і результати додати.
2) Знайди добутки, розклавши другий множник на розрядні доданки:
2 • 48, 3 • 32, 4 • 14.
Розв’язання:
2 • 48 = (2 • 40) + (2 • 8) = 80 + 16 = 96
3 • 32 = (3 • 30) + (3 • 2) = 90 + 6 = 96
4 • 14 = (4 • 10) + (4 • 4) = 40 + 16 = 56
Завдання 835. (Усно.)
4 • 7 = 28
4 • 9 = 36
4 • 11 = 4 • (10 + 1) = 40 + 4 = 44
4 • 13 = 4 • (10 + 3) = 40 + 12 = 52
4 • 15 = 4 • (10 + 5) = 40 + 20 = 60
4 • 17 = 4 • (10 + 7) = 40 + 28 = 68
4 • 19 = 4 • (10 + 9) = 40 + 36 = 76
4 • 21 = 4 • (20 + 1) = 80 + 4 = 84
4 • 23 = 4 • (20 + 3) = 80 + 12 = 92
4 • 25 = 4 • (20 + 5) = 80 + 20 = 100
Завдання 836. (Усно.) Склади і розв'яжи задачу.
|
Погодинний заробіток |
Час |
Разом |
|
16 грн 14 грн |
5 год 6 год |
? |
Перший робітник за годину заробляє 16 грн., а другий – 14 грн. Перший робітник працював 5 год , другий – 6 год. Скільки грошей заробили два робітники разом?
Розв’язання: вираз (16 • 5) + (14 • 6)
16 • 5 = 80 (грн) - заробив перший робітник.
14 • 6 = 84 (грн) - заробив другий робітник.
80 + 84 = 164 (грн) - заробили два робітники разом.
Відповідь: 164 гривні.
Завдання 837. Склади істинні рівності з виразів та їх значень ( 7, 9, 80, 79, 64, 4).
4 • 16 62 – 11 • 5 9 • 11 – 20
80 : 20 2 • 48 – 16 63 : 7 + 0
Розв’язання:
4 • 16 = 64
80 : 20 = 4
62 – 11 • 5 = 7
2 • 48 – 16 = 80
9 • 11 – 20 = 79
63 : 7 + 0 = 9
Завдання 838. Один оператор за 8 год набирає на комп'ютері 32 сторінки тексту. Інший оператор за той самий час набирає 40 сторінок. Який оператор набере за 1 год більше сторінок і на скільки більше?
Розв’язання:
1 спосіб. Вираз (32 : 8) – (40 : 8)
32 : 8 = 4 (с.) - набирає сторінок перший оператор за 1 год.
40 : 8 = 5 (с.) - набирає сторінок другий оператор за 1 год.
5 – 4 = 1 (с.) - на стільки більше сторінок набирає за 1 год другий оператор, ніж перший.
2 спосіб. Вираз (40 – 32) : 8
40 – 32 = 8 (с.) - на стільки більше сторінок набирає другий оператор за 8 год.
8 : 8 = 1 (с.) - на стільки більше сторінок набирає за 1 год другий оператор, ніж перший.
Відповідь: на 1 сторінку.
Завдання 839. 15 г крейди згодували п'яти куркам за день. Скільки потрібно крейди, щоб задовольнити денну потребу в ній 27 курей?
Розв’язання: вираз (15 : 5) • 27
15 : 5 = 3 (г) - крейди давали одній курці на день.
27 • 3 = 81 (г) - потрібно крейди.
Відповідь: 81 грам.
Завдання 840*. У трьох братів 22 олівці. У старшого — у 2 рази більше, ніж у молодшого, а в середнього — на 2 олівці більше, ніж у молодшого. Скільки олівців у кожного брата?
Розв’язання:
1 спосіб.
22 – 2 = 20 (ол.) - олівців порівно у чотирьох пачках (дві у старшого брата, одна у середнього, одна у молодшого)
20 : 4 = 5 (ол.) - олівців у молодшого брата.
5 • 2 = 10 (ол.) - олівців у старшого брата.
5 + 2 = 7 (ол.) - олівців у середнього брата.
2 спосіб.
Нехай х олівців у молодшого брата, тоді
2 • х олівців у старшого брата,
х + 2 олівців у середнього брата.
Складемо рівняння
2х + х + х + 2 = 22
4 х + 2 = 22
4х = 22 – 2
4х = 20
х = 20 : 4
х = 5
У молодшого брата 5 олівців.
5 + 2 = 7 , середнього – 7 олівців,
5 • 2 = 10 , у старшого – 10 олівців .
Відповідь: 5 олівців, 7 олівців, 10 олівців.
Завдання 841°.
2 • 35 : 10 = 70 : 10 = 7
3 • 24 : 9 = 72 : 9 = 8
(24 + 18) : 6 = 42 : 6 = 7
43 • 2 – 18 = 86 – 18 = 68
15 • 5 – 16 = 75 – 16 = 59
(35 + 10) : 5 = 45 : 5 = 9
(13 + 17) • 3 = 30 • 3 = 90
13 + 17 • 3 = 13 + 51 = 64
(98 – 50) : 8 = 48 : 8 = 6
Завдання 842°. Маса шланга завдовжки 1 м становить 3 кг. Яка маса двох таких шлангів завдовжки 13 м кожний?
Розв’язання:
1 спосіб. Вираз (2 • 3) • 13
2 • 3 = 6 (кг) - маса двох шлангів завдовжки 1 м.
6 • 13 = 78 (кг) - маса двох шлангів завдовжки 13 м кожний.
2 спосіб. Вираз (13 • 3) • 2
13 • 3 = 39 (кг) - маса шланга завдовжки 13 м.
39 • 2 = 78 (кг) - маса двох таких шлангів.
Відповідь: 78 кілограми.
Завдання 843. Склади вирази та постав їх значення в порядку зменшення і прочитаєш назву одного з найкрасивіших птахів України.
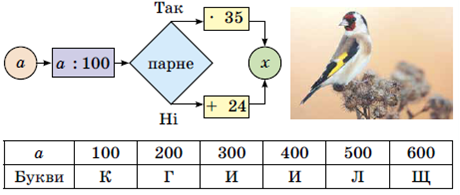
Розв’язання:
(К) 100 : 100 + 24 = 25
(Г) 200 : 100 • 35 = 70
(И) 300 : 100 + 24 = 27
(И) 400 : 100 • 35 = (4 • 30) + (4 • 5) = 120 + 20 = 140
(Л) 500 : 100 + 24 = 29
(Щ) 600 : 100 • 35 = (6 • 30) + (6 • 5)=180 + 30 = 210
210, 140, 70, 29, 27, 25 – ЩИГЛИК
Завдання 844. (Усно.)
3 • 7 = 21
3 • 9 = 27
3 • 11 = 33
3 • 15 = 45
3 • 19 = 57
3 • 23 = 69
3 • 27 = 81
3 • 29 = 87
3 • 32 = 96
Завдання 845. 1) Розв'яжи задачу двома способами. До магазину завезли по 8 ящиків хурми і бананів. Маса ящика хурми — 9 кг, а бананів — 15 кг. На скільки кілограмів більше привезли бананів, ніж хурми?
Розв’язання:
1 спосіб. Вираз (15 – 9) • 8
15 – 9 = 6 (кг) - на стільки більше у ящику бананів,ніж хурми.
6 • 8 = 48 (кг) - на стільки більше привезли бананів, ніж хурми.
2 спосіб. Вираз 15 • 8 – 9 • 8
9 • 8 = 72 (кг) - привезли хурми до магазину.
15 • 8 = 120 (кг) - привезли бананів до магазину.
120 – 72 = 48 (кг) - на стільки більше привезли бананів, ніж хурми.
Відповідь: 48 кілограмів.
2) Поясни складання рівності. (15 – 9) • 8 = 15 • 8 – 9 • 8
Щоб помножити різницю на число, можна помножити на це число зменшуване і від'ємник окремо і від першого добутку відняти другий. (а — b) • с = а • с — b • с — ця рівність виражає розподільний закон множення стосовно віднімання.
3) Перевір, чи істинна рівність (а – b) • с = а • с – b • с, якщо а = 10, b = 6, с = 5.
Розв’язання:
(10 – 6) • 5 = 4 • 5 = 20
(10 • 5) – (6 • 5) = 50 – 30 = 20
Завдання 846. Доповни умову задачі: «Майстер за кожну з п'яти змін виготовляв 24 деталі, а його учень — 15 деталей». Доповніть різними запитаннями так, щоб задачі розв'язувалися за схемами:
1) (□ + □) • □;
2) (□ - □) • □
Розв’язання:
1) Скільки деталей виготовили майстер і учень разом за 5 змін?
2) На скільки більше деталей виготовив за 5 змін майстер, ніж учень.
На скільки меньше деталей виготовив за 5 змін учень, ніж майстер.
Завдання 847. Порівняй вирази, не виконуючи дій.
(45 - 37) • 23 □ 45 • 23 + 37 • 23
5 • (24 + 47) □ 5 • 24 – 5 • 47
6 • (64 – 25) □ 6 • 64 – 25
18 • (73 – 68) □ 18 • 73 – 18 • 68
Розв’язання:
(45 – 37) • 23 < 45 • 23 + 37 • 23
5 • (24 + 47) > 5 • 24 – 5 • 47
6 • (64 - 25) < 6 • 64 – 25
18 • (73 – 68) = 18 • 73 – 18 • 68
Завдання 848*. Знайди ознаку спільних елементів множин А і В.
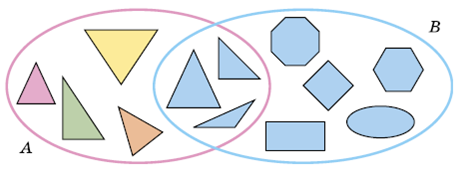
Розв’язання:
Спільними елементами множин є блакитні трикутники.
Завдання 849°. У двох будинках по чотири під'їзди. У першому будинку в кожному під'їзді 27 квартир, а в другому — 36 квартир. На скільки квартир більше у другому будинку, ніж у першому? Розв'яжи задачу двома способами.
Розв’язання:
1 спосіб. Вираз (36 – 27) • 4
36 – 27 = 9 (к.) - на стільки більше квартир у під'їзді другого будинку,ніж першого.
9 • 4 = 36 (к.) - на стільки більше квартир у другому під'їзді, ніж у першому.
2 спосіб. Вираз 36 • 4 – 27 • 4
36 • 4 = 144 (к.) - квартир у першому будинку.
27 • 4 = 108 (к.) - квартир у другому будинку.
144 – 108 = 36 (к.) - на стільки більше квартир у другому будинку, ніж у першому.
Відповідь: 36 квартир.
Завдання 850°.
43 • 3 – 28 = (40 • 3) + (3 • 3) – 28 = 120 + 9 – 28 = 129 – 28 = 101
(18 + 17) • 4 = 35 • 4 = (30 • 4) + (5 • 4) = 120 + 20 = 140
3 • 24 : 8 = 72 : 8 = 9
(43 – 28) • 3 = 15 • 3 = 45
18 + 17 • 4 = 18 + 68 = 86
45 • 2 : 10 = 90 : 10 = 9
(25 + 10) : 5 = 35 : 5 = 7
35 + 10 : 5 = 35 + 2 = 37
4 • 16 : 1 = 64