Завдання 951°. Для виготовлення 3 кг масла витратили 75 л молока. Скільки кілограмів масла можна одержати зі 100 л молока?
1 спосіб. Вираз 100 : (75 : 3)
75 л молока – 3 кг масла
100 л молока - ? кг масла.
75 : 3 = 25 (л) - молока витратили для виготовлення 1 кг масла.
100 : 25 = 4 (кг) - можна одержати масла.
2 спосіб. Вираз (3000 : 75) • 100
75 л молока – 3000 г масла
100 л молока - ? г масла.
3000 : 75 = 40 (кг) – масла буде з 1 л молока.
40 • 100 = 4000 (г) = 4 (кг) - можна одержати масла.
Відповідь: 4 кілограми.
Завдання 952. (Усно.) З виразів на множення та їх результатів склади рівності з діленням на двоцифрове число.
Розв'язання:
24 • 3 = 72 34 • 2 = 68 17 • 5 = 85
72 : 24 = 3 68 : 34 = 2 95 : 17 = 5
Завдання 953. Склади числові вирази за таблицею та обчисли.
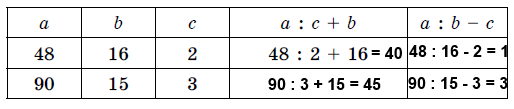
Завдання 954.
|
х • 16 = 80 х = 80 : 16 х = 5 5 • 16 = 80 |
54 : х = 3 х = 54 : 3 х = 18 54 : 18 = 3 |
х : 15 = 3 х = 3 • 15 х = 45 45 : 15 = 3 |
Завдання 955. Дві кравчині мають пошити по 96 сорочок. Одна з них шиє за день 12 сорочок, а друга — 16. Яка кравчиня виконає роботу раніше і на скільки днів?
Розв'язання: вираз 96 : 12 – 96 : 16
96 : 12 = 8 (д.) - днів треба першій кравчині.
96 : 16 = 6 (д.) - днів треба другій кравчині.
8 – 6 = 2 (д.) - на стільки днів швидше виконає роботу друга кравчиня, ніж перша.
Відповідь: 2 дні.
Завдання 956. Токар виготовив 100 деталей. Перші 3 год він робив по 12 деталей за годину, а потім почав виготовляти по 16 деталей за годину. Скільки годин токар виготовляв по 16 деталей?
Розв'язання: вираз (100 – 3 • 12) : 4
3 • 12 = 36 (д.) - зробив токар деталей спочатку.
100 – 36 = 64 (д.) - залишилося зробити деталей.
64 : 16 = 4 (год) - працював годин токар потім.
Відповідь: 4 години.
Завдання 957*. За рік будівельники повинні збудувати 72 виставкових павільйони. Перші три квартали вони будували по 18 павільйонів. У жовтні й листопаді — по 6 павільйонів, а в грудні — 8. Чи виконали будівельники річне зобов'язання?
Розв'язання: вираз 3 • 18 + 2 • 6 + 8
18 • 3 = 54 (п.) - побудували павільйонів у перші три квартали.
6 • 2 = 12 (п.) - побудували павільйонів у жовтні та листопаді.
54 + 12 + 8 = 74 (п.) - побудували павільйонів за весь час.
74 – 72 = 2 (п.) - перевиконали річне зобов'язання.
Відповідь: так.
Завдання 958°.
45 : 5 = 9
32 : 8 = 4
70 : 14 = (28 + 42) : 14 = (28 : 14) + (42 : 14) = 2 + 3 = 5
42 : 21 = (21 + 21) : 21 = (21 : 21) + (21 : 21) = 1 + 1 = 2
2 • 37 = 2 • (30 + 7) = (2 • 30) + (2 • 7) = 60 + 14 = 74
54 : 18 = (18 + 36) : 18 = (18 : 18) + (36 : 18) = 1 + 2 = 3
28 : 4 + 3 • 7 = 7 + 21 = 28
540 : 3 + 180 = (240 + 300) : 3 + 180 = (240 : 3) + (300 : 3) + 180 = 80 + 100 + 180 = 360
Завдання 959°. Маса шести коробок з печивом 48 кг. Яка маса восьми коробок із цукерками, якщо коробка із цукерками на 3 кг важча від коробки з печивом?
Розв'язання: вираз (48 : 6 + 6) • 6
48 : 6 = 8 (кг) - вага одної коробки з печивом.
8 + 3 =11 (кг) - вага одної коробки із цукерками.
11 • 8 = 88 (кг) - вага коробок з цукерками.
Відповідь: 88 кілограмів.
Завдання 960. Порівняй, як змінюється добуток при зміні одного з множників у кілька разів.


Завдання 961.
|
12 • 3 = 36 3 • 17 = 51 13 • 4 = 52 25 • 6 = 150 26 • 3 = 78 |
12 • 18 = 12 • (3 • 6) = 36 • 6 = 216 15 • 17 = (3 • 5) • 17 = 51 • 5 = 255 130 • 4 = (13 • 10) • 4 = 52 • 10 = 520 25 • 18 = 25 • (6 • 3) = 150 • 3 = 450 260 • 3 = (10 • 26) • 3 = 10 • 72 = 780 |
Завдання 962.
1) У виразі 24 • 6 один з множників збільш у 2 рази, а другий зменш у 2 рази і порівняй добутки.
24 • 6 = 20 • 6 + 4 • 6 = 144
48 • 3 = 40 • 3 + 8 • 3 = 144
144 = 144 , добутки рівні
2) Порівняй множники і добутки у стовпчиках і зроби висновок.
24 • 6 = (20 • 6) + (4 • 6) = 144
72 • 2 = (70 • 2) + (2 • 2) = 144
144 = 144 , добутки рівні
20 • 8 = 160
40 • 4 = 160
160 = 160, добутки рівні
9 • 15 = (9 • 10) + (9 • 5) =135
27 • 5 = (20 • 5) + (7 • 5) = 135
135 = 135, добутки рівні

Завдання 963. Обчисли за зразком і зроби висновок про спосіб множення на 5.
18 • 5 = (18 : 2) • (5 • 2) = 9 • 10 = 90
Розв'язання:
14 • 5 = (14 : 2) • (5 • 2) = 7 • 10 = 70
24 • 5 = (24 : 2) • (5 • 2) = 12 • 10 = 120
46 • 5 = (46 : 2) • (5 • 2) = 23 • 10 = 230
28 • 5 = (28 : 2) • (5 • 2) = 14 • 10 = 140
Щоб помножити деяке число на 5, можна число спочатку поділити на 2, потім помножити на 10.
Завдання 964. Квітникарка склала 8 букетів по 5 троянд і 6 букетів по 5 гвоздик. Скільки всього квітів використала квітникарка?
Розв'язання:
1 спосіб. Вираз (5 • 8) + (5 • 6)
5 • 8 = 40 (к.) - використала троянд.
5 • 6 = 30 (к.) - використала гвоздик.
40 + 30 = 70(к.) - використала квітів разом.
2 спосіб. Вираз 5 • (8 + 6)
8 + 6 = 14 (б.) - склала букетів разом.
5 • 14 = 70 (к.) - використала квітів разом.
Відповідь: 70 квітів.
Склади і розв'яжи обернену задачу.
Квітникарка мала 70 квітів. Вона склала 8 букетів троянд і 6 букетів гвоздик, з однаковою кількістю квітів у букетах. Кільки квітів було в одному букеті?
Розв'язання: Вираз 70 : (8 + 6)
8 + 6 = 14 (б.) - склала букетів разом.
70 : 14 = 5 (к.) - квітів було в одному букеті.
Відповідь: 5 квітів.
Завдання 965. В авіаційному училищі 320 курсантів. 80 курсантів літають з інструктором, у 2 рази менше курсантів — самостійно, а решта ще вчаться на тренажерах. Скільки курсантів вчаться на тренажерах?
Розв'язання: вираз 320 – (80 + 80 : 2)
80 : 2 = 40 (к.) - курсантів вчаться самостійно.
80 + 40 = 120 (к.) - курсантів літають з інструктором та вчаться самостійно.
320 – 120 = 200 (к.) - курсантів вчаться на тренажерах.
Відповідь: 200 курсантів.
Заміни слово «менше» словом «більше». Чи зміниться план розв'язування задачі?
В авіаційному училищі 320 курсантів. 80 курсантів літають з інструктором, у 2 рази більше курсантів — самостійно, а решта ще вчаться на тренажерах. Скільки курсантів вчаться на тренажерах?
Розв'язання: вираз 320 – (80 + 80 • 2)
80 • 2 = 160 (к.) - курсантів вчаться самостійно.
80 + 160 = 240 (к.) - курсантів літають з інструктором та вчаться самостійно.
320 – 240 = 80 (к.) - курсантів вчаться на тренажерах.
Відповідь: 80 курсантів.
Завдання 966*. 12 третьокласників брали участь у змаганнях з бігу, 10 - зі стрибків, а 5 учнів — з бігу і стрибків. Скільки всього третьокласників брали участь у змаганнях?
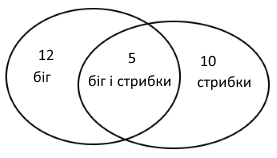
Розв'язання:
1 спосіб вираз 12 – 5 + 10
12 – 5 = 7 (уч.) - учнів брали участь у змаганнях тільки з бігу.
7 + 10 = 17 (уч.) - учнів у класі.
2 спосіб вираз 10 - 5 + 12
10 – 5 = 5 (уч.) - учнів брали участь у змаганнях тільки зі стрибків.
5 + 12 = 17 (уч.) - учнів у класі.
3 спосіб вираз 12 + 10 – 5
12 + 10 = 22 (уч.) - учнів брали участь у змаганнях тільки з бігу, тільки зі стрибків, з бігу та стрибків разом.
22 – 5 = 17 (уч.) - учнів у класі.
Відповідь: 17 учнів.
Завдання 967°.
46 • 5 = (46 : 2) • 10 = 23 • 10 = 230
32 • 5 = (32 : 2) • 10 = 16 • 10 = 160
94 + 5 = 99
78 + 5 = 83
4 • 24 – 38 : 2 = 4 • (20 + 4) – (30 + 8) : 2 = 80 + 16 – (15 + 4) = 96 – 19 = 77
5 • 26 + 48 • 5 = 5 • (26 + 48) = 74 • 5 = (74 : 2) • 10 = 37 • 10 = 370
36 • 10 = 360
72 • 5 = (72 : 2) • 10 = 36 • 10 = 360
Завдання 968°. У парку 240 кущів бузку. На кінець квітня розквітло 60 кущів білого бузку, а рожевого — у 2 рази більше. Скільки кущів бузку ще не розквітло?
Розв'язання: вираз 240 – (60 + 60 • 2)
60 • 2 = 120 (к.) - розквітло кущів рожевого бузку.
60 + 120 = 180 (к.) - розквітло кущів білого та рожевого бузку разом.
240 – 180 = 60 (к.) - кущів бузку ще не розквітло.
Відповідь: 60 кущів.
Завдання 969.
360 : 10 = 36
800 : 100 = 8
900 : 10 = 90
480 : 4 = 120
Завдання 970. Порівняй, як змінюється частка внаслідок збільшення (зменшення) діленого в кілька разів.
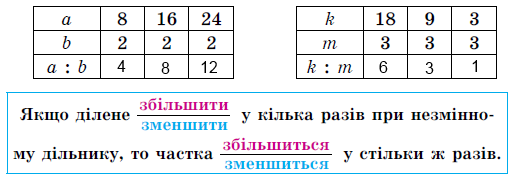
Завдання 971. Порівняй вирази у кожному стовпчику. Знайди значення виразів нижнього рядка, використовуючи значення відповідних виразів верхнього.
Розв'язання:
|
36 : 3 = 12 72 : 8 = 9 96 : 16 = 6 75 : 25 = 3 |
360 : 3 = (36 • 10) : 3 = 12 • 10 = 120 720 : 8 = (72 • 10) : 8 = 9 • 10 = 90 960 : 16 = (96 • 10) : 16 = 6 • 10 = 60 750 : 25 = (75 • 10) : 25 = 5 • 10 = 30 |
Завдання 972. З однієї грядки зібрали 15 кг цибулі, а з другої - у 3 рази більше. Усю цибулю розклали в сітки по 5 кг. Скільки сіток із цибулею?
Розв'язання: вираз (15 + 15 • 3) : 5
15 • 3 = 45 (кг) - цибулі зібрали з другої грядки.
15 + 45 = 60 (кг) - цибулі зібрали разом.
60 : 5 = 12 (с.) - було сіток з цибулею.
Відповідь: 12 сіток.
Розв'яжи задачу за схемою: □ : □ + (□ : □) • □.
Розв'язання: вираз 15 : 5 + (15 : 5) • 3
15 : 5 = 3 (с.) - було сіток із цибулею першої грядки.
15 : 5 • 3 = 9 (с.) - було сіток із цибулею другої грядки.
3 + 9 = 12 (с.) - було сіток з цибулею.
Відповідь: 12 сіток.
Завдання 973. Бабуся повісила на горищі сушити 15 пучків трави звіробою, м'яти — на 5 пучків менше, а кропиви — стільки, скільки звіробою і м'яти разом. Скільки пучків кропиви заготовила бабуся?
Розв'язання: вираз 15 + (15 – 5)
15 – 5 = 10 (п.) - пучки м’яти.
15 + 10 = 25 (п.) - пучки кропиви.
Відповідь: 25 пучків.
Завдання 974*. Скільки буде десятків, якщо 2 десятки помножити на 4 десятки?
Розв'язання:
20 • 40 = 2 • 10 • 4 • 10 = 8 • 100 = 800
2 дес. • 4 дес. = 80 дес.
2 • 1 дес. • 4 • 1 дес. = 8 • 10 дес. = 80 дес.
Завдання 975°. Діти зібрали і здали в аптеку 4 кг квітів мати-й-мачухи, 8 кг березових бруньок, а молодих пагінців сосни — у 5 разів більше, ніж квітів мати-й-мачуха та березових бруньок разом. Скільки кілограмів пагінців сосни зібрали діти?
Розв'язання: вираз (4 + 8) • 5
4 + 8 = 12 (кг) - зібрали квітів мати-й-мачухи та березових бруньок разом.
12 • 5 = 60 (кг) - зібрали пагінців сосни.
Відповідь: 60 кілограмів.