Завдання 1051. Скільки окремих квадратів можна скласти з 11 однакових паличок? (Перевір розв'язання задачі практично.)
Розв'язання:
11 : 4 = 2 (ост. 3).
Відповідь: 2 квадрати.
Завдання 1052. Скільки окремих трикутників можна скласти з 11 однакових паличок?
Розв'язання:
11 : 3 = 3 (ост. 2).
Відповідь: 3 трикутники.
Завдання 1053.

Завдання 1054*. Діти зважували своїх домашніх тварин парами. Мурчик і Тузик разом важать 19 кг, Мурчик і Бобик разом важать 27 кг, а Тузик і Бобик — 40 кг. Хто скільки важить?
Розв'язання:
1 спосіб.
19 + 27 + 40 = 86 (кг) – важили би 2 Мурчики, 2 Тузики, 2 Бобики разом.
86 : 2 = 43 (кг) – важать Мурчик, Тузик, Бобик разом.
43 – 40 = 3 (кг) – важить Мурчик.
43 – 27 = 16 (кг) – важить Тузик.
43 – 19 = 24 (кг) – важить Бобик.
2 спосіб.
19 + 27 = 46 (кг) - важать Мурчик і Тузик, Мурчик і Бобик.
46 – 40 = 6 (кг) - важить Мурчик, зважений двічі.
6 : 2 = 3 (кг) - важить Мурчик.
19 – 3 = 16 (кг) - важить Тузик.
27 – 3 = 24 (кг) - важить Бобик.
Відповідь: 3 кг, 16 кг, 24 кг.
Завдання 1055°.
|
15 : 5 = 3 16 : 5 = 3 (ост.1) |
30 : 6 = 5 32 : 6 = 5 (ост.2) |
45 : 9 = 5 48 : 9 = 5 (ост.3) |
64 : 8 = 8 67 : 8 = 8 (ост.3) |
Завдання 1056°. У першому ящику 20 кг помідорів, а в другому — 12 кг. З другого ящика продали 8 кг помідорів. У скільки разів стало більше помідорів у першому ящику, ніж у другому?
Розв'язання:
12 – 8 = 4 (кг) - залишилося помідорів у другому ящику.
20 : 4 = 5 (р.) - у скільки разів стало більше помідорів у першому ящику, ніж у другому.
Відповідь: 5 разів.
Завдання 1057. Виконай ділення з остачею.
27 : 6 Зразок міркування. Нехай треба поділити 27 на 6. Знайдемо найбільше із чисел від 1 до 27, яке ділиться націло на 6. Це 24; 24 : 6 = 4. Знайдемо остачу: 27 - 24 = 3. Отже, 27 : 6 = 4 (ост. 3).
| 48 : 7 = 6 (ост. 6) | 54 : 8 = 6 (ост. 6) | 20 : 6 = 3 (ост. 2) |
Завдання 1058. Чашка коштує 8 грн. Скільки таких чашок можна купити на 35 грн?
Розв'язання:
35 : 8 = 4 (ост. 3).
Відповідь: 4 чашки.
Завдання 1059. Для посадки привезли 24 саджанці яблунь і 8 саджанців груш. 1/4 усіх саджанців посадили діти, а решту — дорослі. Скільки саджанців посадили дорослі?
Розв'язання:
24 + 8 = 32 (с.) - привезли саджанців яблунь та груш разом.
32 : 4 • 1 = 8 (с.) - посадили саджанців діти.
32 – 8 = 24 (с.) - посадили саджанців дорослі.
Відповідь: 24 саджанці.
Завдання 1060. Туристи поїздом проїхали 240 км, автобусом — на 180 км менше, ніж поїздом, а пішки пройшли 1/5 того шляху, який проїхали автобусом. Скільки кілометрів туристи пройшли пішки?
Розв'язання:
240 – 180 = 60 (км)- туристи проїхали автобусом.
60 : 5 • 1 = 12 (км) - пройшли пішки.
Відповідь: 12 кілометрів.
Завдання 1061.
|
х - 48 : 6 = 204 х – 8 = 204 х = 204 + 8 х = 212 212 – 48 : 6 = = 212 – 8 = 204 204 = 204 |
23 • 5 – х = 42 115 – х = 42 х = 115 – 42 х = 73 23 • 5 – 73 = = 115 – 73 = 42 42 = 42 |
|
х : 6 = 305 – 297 х : 6 = 8 х = 6 • 8 х = 48 48 : 6 = 8 305 – 297 = 8 8 = 8 |
600 : х = 34 + 26 600 : х = 60 х = 600 : 60 х = 10 600 : 10 = 60 34 + 26 = 60 60 = 60 |
|
х • (38 – 29) = 72 х • 9 = 72 х = 72 : 9 х = 8 8 • (38 – 29) = = 8 • 9 = 72 72 = 72 |
6 • х = 720 : 8 6 • х = 90 х = 90 : 6 х = 15 6 • 15 = 90 720 : 8 = 90 90 = 90 |
Завдання 1062. Склади і запиши три вирази на ділення з дільником 8, щоб при обчисленні першого виразу остача дорівнювала 0, другого — 3, а третього — 7.
Розв'язання:
| 80 : 8 = 10 | 83 : 8 = 10 (ост. 3) | 87 : 8 = 10 (ост. 7) |
Завдання 1063*. У гаражі стоїть 30 автомобілів. Вантажні автомобілі мають по 6 коліс, а легкові — по 4. Скільки яких автомобілів у гаражі, якщо всього коліс 168?
Розв'язання:
1 спосіб.
4 • 30 = 120 (к.) – всього коліс по 4 шт.
168 – 120 = 48 (к.) – додаткові по 2 колеса у вантажних автомобілях..
48 : 2 = 24 (г.) – вантажних автомобілів.
30 – 24 = 6 (л.) – легкових автомобілів.
2 спосіб.
Нехай х – легкові автомобілі, тоді 30 – х – вантажні автомобілі. Складемо рівняння
х • 4 + (30 – х) • 6 = 168
4 • х + 180 – 6 • х = 168
180 + 4 • х – 6 • х = 168
180 + 4 • х – 4 • х – 2 • х = 168
180 – 2 • х = 168
2 • х = 180 – 168
2 • х = 12
х = 12 : 2
х = 6
У гаражі було 6 легкових та 30 - 6 = 24 вантажних автомобілів.
Відповідь: 6 легкових, 24 вантажних автомобілів.
Завдання 1064°. Виконай ділення з остачею.
22 : 7 = 3 (ост. 1)
12 : 5 = 2 (ост. 2)
40 : 7 = 5 (ост. 5)
14 : 3 = 4 (ост. 2)
50 : 7 = 7 (ост. 1)
21 : 6 = 3 (ост. 3)
60 : 7 = 8 (ост. 4)
25 : 4 = 6 (ост. 1)
75 : 6 = 12 (ост. 3)
33 : 8 = 4 (ост. 1)
Завдання 1065°. У фермера були качки й гуси. Усього 60 птахів. Гуси становили шосту частину всіх птахів. Скільки було качок?
Розв'язання:
1 спосіб.
60 : 6 = 10 (п.) - було гусей.
60 – 10 = 50 (п.) - було качок.
2 спосіб.
60 : 6 = 10 (п.) – птахів припадає на 1 частину.
6 – 1 = 5 (часть) – частин припадає на качок.
10 • 5 = 50 (п.) – качок у фермера.
Відповідь: серед птахів 50 качок.
Завдання 1066. Склади істинні рівності за блок-схемами.
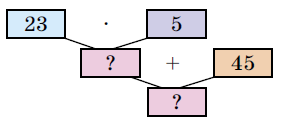
23 • 5 + 45 = (20 + 3) • 5 + 45 = 100 + 15 + 45 = 160
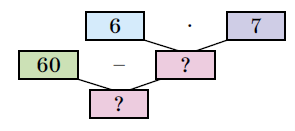
60 – (6 • 7) = 60 – 42 = 18
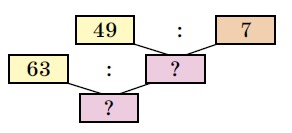
63 : (49 : 7) = 63 : 7 = 9
Завдання 1067. Перевір, чи правильно знайдено остачі при діленні на 2, 3, 4, 5, і зроби висновок.
Остачі знайдено правильно.
Якими цифрами закінчуються числа, які діляться на 2 без остачі? А на 5?
Розв'язання:
Числа, які діляться на 2 без остачі, закінчуються парною цифрою.
Числа, які діляться на 5 без остачі, закінчуються цифрою 5 або 0.
Завдання 1068. Яка найбільша остача може бути при діленні на 7; на 9?
При діленні остача завжди менша за дільник.
Розв'язання:
При діленні на 7 найбільша остача може бути 6;
при діленні на 9 найбільша остача може бути 8.
Завдання 1069. У хорі 36 дітей. Дев'ята частина всіх дітей — хлопчики, а решта — дівчатка. На скільки більше в хорі дівчаток, ніж хлопчиків?
Розв'язання:
36 : 9 = 4 (д.) - хлопчики у хорі.
36 – 4 = 32 (д.) - дівчата у хорі.
32 – 4 = 28 (д.) - на стільки більше в хорі дівчаток, ніж хлопчиків.
Відповідь: на 28 дітей.
Завдання 1070. Добери значення змінних, щоб нерівності були істинними.
| х • 6 < 86 - 58 | х : 7 > 42 : 7 | 64 – х < 34 |
Розв'язання:
|
х • 6 < 86 – 58 х • 6 < 28 х = 1, 2, 3, 4 |
х : 7 > 42 : 7 Частка більша там, де більше ділене х > 42 х = 49, 56, 63 |
64 – х < 34 64 – х < 64 – 30 Разность меньше там, где больше вычитаемое. х > 30 х = 31, 32, 33, … |
Завдання 1071. Першого дня майстер виготовив 10 деталей, що становить п’яту частину замовлення, а другого 1/4 решти. Скільки деталей виготовив майстер другого дня?
Розв'язання:
10 • 5 = 50 (д.) - замовлення для майстра.
50 – 10 = 40 (д.)- решта деталей після першого дня.
40 : 4 • 1 = 10 (д.) - виготовив майстер другого дня.
Відповідь: 10 деталей.
Зміни запитання, щоб у розв'язанні додалася ще одна дія.
Скільки деталей виготовив майстер за два дні?
10 + 10 = 20 (д.) - деталей виготовив майстер за два дні.
Завдання 1072*. Гра. Гравців двоє. У купці 10 сірників. За один хід гравець може брати 1 або 3 сірники. Виграє той, хто візьме один останній сірник. Скільки сірників на початку повинен узяти перший гравець, щоб виграти?
Розв'язання:
10 - 1 = 9 (с.) - сірників повинні вибрати два гравці.
Щоб виграв перший гравець, к-сть ходів має бути парна.
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1 + 3
1 + 1 + 1 + 3 + 3
3 + 3 + 3
Отже, при будь-якому розкладу 9 на доданки їх буде непарне число, тобто останнім сірник завжди буде брати другий гравець. Перший гравець завжди буде у програші.
Завдання 1073°. Дівчинка витратила 3 грн, що становить п'яту частину всіх її грошей. На скільки більше грошей залишилося, ніж вона витратила?
Розв'язання:
3 • 5 = 15 (грн) - було грошей у дівчинки.
15 – 3 = 12 (грн) - залишилося грошей у дівчинки.
12 – 3 = 9 (грн) - на стільки більше грошей залишилося, ніж вона витратила.
Відповідь: 9 гривень.
Завдання 1074°.
|
х : (450 – 390) = 4 х : 60 = 4 х = 60 • 4 х = 240 240 : (450 – 390) = 240 : 60 = 4 4 = 4 |
56 : х = 800 : 100 56 : х = 8 х = 56 : 8 х = 7 56 : 7 = 8 800 : 100 = 8 8 = 8 |
|
39 – х = 49 : 7 39 – х = 7 х = 39 – 7 х = 32 39 – 32 = 7 49 : 7 = 7 7 = 7 |
(360 : 6) : х = 4 60 : х = 4 х = 60 : 4 х = 15 (360 : 6) : 15 = 60 : 15 = 4 4 = 4 |
Завдання 1075. Знайди:
1/5 від 2 м;
1/10 від 3 ц;
1/6 від 2 діб.
Розв'язання:
2 м : 5 • 1 = 200 см : 5 • 1 = 40 см
3 ц : 10 • 1 = 300 кг : 10 • 1 = 30 кг
2 доби : 6 • 1 = 2 • 24 год : 6 • 1 = 48 год : 6 = 8 год