Завдання 1076. Використовуючи вирази на ділення, склади рівності.
36 : 7 = 5 (ост. 1) 38 : 6 = 6 (ост. 2) 53 : 9 = 5 (ост. 8)
36 = 5 • 7 + 1 38 = 6 • 6 + 2 53 = 5 • 9 + 8
Якщо при додаванні остачі до добутку частки й дільника отримаємо ділене, то ділення виконано правильно.
Завдання 1077. Не обчислюючи, знайди помилки.
42 : 6 = 6 (ост. 6) неправильно : остача повинна бути менша, ніж дільник
54 : 7 = 7 (ост. 5) правильно
55 : 6 = 8 (ост. 7) правильно
74 : 9 = 8 (ост. 2) правильно
Завдання 1078. Сторона квадрата а. Запиши рівність для знаходження периметра квадрата.
Розв'язання:
Оскільки квадрат – прямокутник, у якого довжини всіх сторін рівні, маємо
Р = 4 • а
Завдання 1079. Периметр ділянки квадратної форми дорівнює 36 м. Яка довжина сторони ділянки?
Розв'язання:
36 : 4 = 9 (м) - довжина сторони квадратної ділянки.
Відповідь: 9 метрів.
Завдання 1080*. Цуценя важче за котика на 3 кг. Маса двох цуценят така сама, як 5 котиків. Яка маса цуценяти?
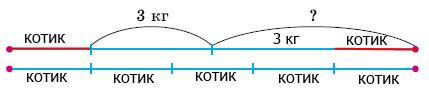
Розв'язання:
Міркуємо так: 1 котик + 3 кг = 1 цуценя, тоді з одного боку
2 • (1 котика + 3 кг) = 2 цуценя.
2 котика + 6 кг = 2 цуценя
З іншого боку 5 котиків = 2 цуценям.
Розглянемо дві ліві частини рівностей, маємо
2 котики + 6 кг = 5 котикам, тоді 3 котики важать 6 кг.
Оскільки маса трьох котиків дорівнює 6 кг, тоді
6 : 3 = 2 (кг) - маса одного котика.
2 + 3 = 5 (кг) - маса цуценяти.
Відповідь: 5 кілограмів.
Завдання 1081°. Виконай ділення з перевіркою.
68 : 9 38 : 5 64 : 3 75 : 2 94 : 9
Розв'язання:
68 : 9 = 7 (ост. 5) 68 = 7 • 9 + 5
38 : 5 = 7 (ост. 3) 38 = 7 • 5 + 3
64 : 3 = 21 (ост. 1) 64 = 21 • 3 + 1
75 : 2 = 37 (ост. 1) 75 = 37 • 2 + 1
94 : 9 = 10 (ост. 4) 94 = 10 • 9 + 4
Завдання 1082°. Маса 6 однакових ящиків з печивом 48 кг. Маса ящика із цукерками на 2 кг більша від маси ящика з печивом. Яка маса 8 ящиків із цукерками?
Розв'язання:
48 : 6 = 8 (кг) - маса одного ящика із печивом.
8 + 2 = 10 (кг) - маса одного ящика із цукерками.
8 • 10 = 80 (кг) - маса цукерок.
Відповідь: 80 кілограмів.
Завдання 1083. Добутком яких двох чисел можна замінити число 10?
10 = 1 • 10
10 = 2 • 5
Кожне число, що складається тільки з десятків і не має окремих одиниць, ділиться на 10, а отже, і на 2, і на 5. Тому подільність чисел на 2 і на 5 без остачі залежить лише від останньої цифри.
На 2 без остачі діляться числа, запис яких закінчується цифрами 0, 2, 4, 6, 8.
На 5 без остачі діляться числа, запис яких закінчується цифрою 5 або 0.
Завдання 1084. Не обчислюючи, визнач, які числа діляться без остачі на 2, а які на 5: 232, 483, 645, 780, 896, 915.
Розв'язання:
На 2 без остачі діляться числа: 232, 780, 896.
На 5 без остачі діляться числа: 645, 780, 915.
Завдання 1085. Перший трактор за 7 год роботи витрачає 56 л пального, а другий — за 1 год витрачає на 2 л менше. Скільки літрів пального витрачає другий трактор за 7 год? (Розв'яжи задачу двома діями.)
Розв'язання:
7 • 2 = 14 (л) - на стільки менше пального витратить другий трактор за час роботи.
56 – 14 = 42 (л) - пального витрачає другий трактор за 7 год. роботи.
Відповідь: 42 літри.
Завдання 1086. Поясни складання нерівностей.
5 • х = 10 х • 8 = 24 х : 2 = 10
5 • х > 8 х • 8 < 32 х : 2 < 10
5 • х < 11 х • 8 > 16 х : 2 > 8
8 < 5 • х < 11 16 < х • 8 < 32 8 < х : 2 < 10
Для складання нерівностей використовують знаки нерівностей
> більше, < менше , = рівне
Завдання 1087*. Двом братам разом 20 років. Один з них у 4 рази старший. Скільки років кожному?
Розв'язання:
1 спосіб.
Умовно можна уявити, що на молодшого брата припадає 1 частина років, а на старшого – 4 такі частини, таким чином маємо для двох братів разом 5 частин, тоді
20 : 5 = 4 (р.) - років молодшому братові (бо припадає на одну частину).
4 • 4 = 16 (р.) - років старшому братові.
2 спосіб.
Нехай молодшому братові х років, тоді старшому братові 4 • х років. Складемо рівняння
х + 4 • х = 20
(1 + 4) • х = 20
5 • х = 20
х = 20 : 5
х = 4
4 (р.) - років молодшому братові.
4 • 4 = 16 (р.) - років старшому братові.
Відповідь: 4 роки, 16 років.
Завдання 1088. У їдальню привезли 4 мішки білокачанної капусти по 10 кг і 3 мішки цвітної капусти. Скільки кілограмів цвітної капусти в кожному мішку, якщо всього привезли 64 кг капусти?
Розв'язання:
4 • 10 = 40 (кг) - привезли білокачанної капусти.
64 – 40 = 24 (кг) - привезли цвітної капусти.
24 : 3 = 8 (кг) - кілограмів цвітної капусти в одному мішку.
Відповідь: 8 кілограмів.
Яка з блок-схем відповідає розв'язанню задачі?
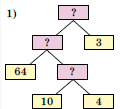
Перша.
Склади обернену задачу за другою блок-схемою.
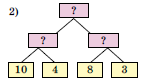
У їдальню привезли 4 мішки білокачанної капусти по 10 кг і 3 мішки цвітної капусти по 8 кг. Скільки кілограмів капусти привезли?
Завдання 1089. Добери значення змінної, щоб нерівності були істинними:
90 < 13 • х < 100; 80 < 12 • а < 90.
Розв'язання:
90 < 13 • 7 < 100, оскільки 13 • 7 = 91
80 < 12 • 7 < 90, оскільки 12 • 7 = 84
Завдання 1090.
59 : 9 = 6 (ост. 5)
76 : 10 = 7 (ост. 6)
811 : 10 = 81 (ост. 1)
87 : 30 = 2 (ост. 27)
Завдання 1091. Побудуй квадрат, периметр якого дорівнює периметру рівностороннього трикутника зі стороною 12 см.
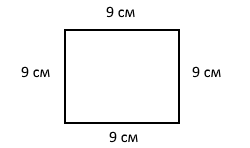
Розв'язання:
3 • 12 = 36 (см) - периметр рівностороннього трикутника.
36 : 4 = 9 (см) - довжина сторони квадрата.
Треба побудувати квадрат зі стороною 9 см.
Завдання 1092. Екскурсія розпочалась об 11 год і тривала 3 год. О котрій годині закінчилась екскурсія?
Розв'язання:
11 + 3 = 14 (год.) - закінчилася екскурсія о такій годині.
Відповідь: о 14 годині.
Завдання 1093°. Магазин розпочинає роботу о 7 год, а закінчує — о 19 год. Скільки годин працює магазин, якщо обідня перерва триває 1 год?
Розв'язання:
19 – 7 – 1 = 11 (год.) - годин працює магазин.
Відповідь: 11 годин.
Нагадаємо, що 1 м = 10 дм = 100 см
1 дм = 10 см = 100 мм
1 см = 10 мм
1 т = 100 ц = 1000 кг
1 ц = 100 кг
1 кг = 1000 г
Завдання 1094°

Розв'язання:
У підручнику помилкова умова, бо 500 к.:3 =... (не ділиться націло). Якщо замість "5 грн" написати "6 грн", то отримаємо:
6 грн : 3 = 2 грн.
2 дм : 4 = 20 см : 4 = 5 см
1 ц 5 кг : 5 = (100 кг + 5 кг) : 5 = 20 кг + 1 кг = 21 кг
2 м 8 дм : 2 = (2 м + 8 дм) : 2 = 1 м + 4 дм = 1 м 4 дм
1 см 8 мм : 3 = 18 мм : 3 = 6 мм
Додаткові вправи
1. Обчисли зручним способом. 48 : (4 • 2) 560 : (8 : 2) 800 : (10 • 8)
48 : (4 • 2) = 48 : 8 = 6
560 : (8 : 2) = (560 : 8) : 2 = 70 : 2 = 35
800 : (10 • 8) = 800 : 8 : 10 = 10
2. 23 • 2 + 1 = 46 + 1 = 47
64 : 4 – 4 = 16 – 4 = 12
48 : 6 + 2 = 8 + 2 = 10
80 : 5 + 0 = 16
48 : (6 + 2) = 48 : 8 = 6
0 : 7 + 70 = 0 + 70 = 70
24 • 4 – 3 = 96 – 3 = 93
51 : 3 + 7 = 17 + 7 = 24
3. 2 м : 5 = 20 дм : 5 = 4 дм
2 дм : 5 = 20 см : 5 = 4 см
2 м – 5 дм = 20 дм – 5 дм = 15 дм
2 дм – 5 см = 20 см – 5 см = 15 см
1 кг : 2 = 1000 г : 2 = 500 г
1 кг : 5 = 1000 г : 5 = 200 г
1 кг – 200 г = 1000 г – 200 г = 800 г
1 кг – 2 г = 1000 г – 2 г = 998 г
4. У дитячий садок привезли яблука. Протягом п'яти днів витрачали по 9 кг яблук щодня. Залишилося на 8 кг більше, ніж витратили. Скільки кілограмів яблук привезли в дитячий садок?
Розв'язання:
5 • 9 = 45 (кг) - витратили яблук.
45 + 8 = 53 (кг) - залишилося яблук.
45 + 53 = 98 (кг) - привезли яблук у дитячий садок.
Відповідь: 98 кілограмів.
5. 36 л соку розлили в банки по 3 л, а 28 л компоту — у банки по 2 л. Скільки всього потрібно було банок?
Розв'язання:
36 : 3 = 12 (б.) - банок потрібно було для соку.
28 : 2 = 14 (б.) - банок потрібно для компоту.
12 + 14 = 26 (б.) - потрібно всього банок.
Відповідь: 26 банок.
Склади обернені задачі.
Сік розлили в 12 банок по 3 л в кожну, а компот — у 14 банок по 2 л в кожну. Скільки всього літрів було соку та компоту?
Було 64 л соку та компоту разом. Сік розлили в 12 банок по 3 л у кожну, компоту — у банки по 2 л у кожну. Скільки потрібно було банок для компоту?
Було 64 л соку та компоту разом. Сік розлили в банки по 3 л кожна, компоту — у 14 банок по 2 л. Скільки потрібно було банок для соку?
6. Склади і розв'яжи задачі за короткими записами.
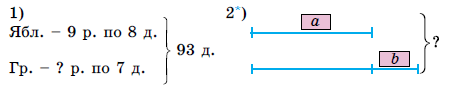
1) У саду посадили 93 фруктових дерев, з них посадили 9 рядів яблунь по 8 дерев у кожному ряду та груші. Скільки посадили рядів груш, якщо у 1 ряд має 7 дерев?
Розв'язання:
9 • 8 = 72 (д.) - посадили яблунь.
93 – 72 = 21 (д.) - посадили груш.
21 : 7 = 3 (р.) - посадили рядів груш.
Відповідь: 3 ряди.
2) Довжина першої ділянки а , друга - на b довша від першої ділянки. Яка довжина двох ділянок?
Розв'язання:
а + b – довжина другої ділянки
a + a + b = 2a + b – довжина двох ділянок.
Відповідь: 2a + b.
7. Якщо стрічку розрізати на 4 частини по 16 м, то залишиться ще 6 м. Але цю стрічку розрізали на частини по 5 м. На скільки частин розрізали стрічку?
Розв'язання:
4 • 16 + 6 = 70 (м.) - довжина стрічки.
70 : 5 = 14 (ч.) - кількість розрізаних частин.
Відповідь: 14 частин.
8. Бригада робітників за нормою повинна збирати 48 пилососів за 4 дні, а збирає їх за 3 дні. Скільки пилососів понад норму збирає за день бригада робітників?
Розв'язання:
48 : 4 = 12 (п.) - норма збору пилососів на 1 день для бригади.
48 : 3 = 16 (п) - збирає пилососів за день бригада.
16 – 12 = 4 (п.) - пилососів понад норму збирає за день бригада.
Відповідь: 4 пилососи.
9. Один хлопець сказав, що в нього братів і сестер порівну, а у його сестри братів удвоє більше, ніж сестер. Скільки дітей у цій сім'ї?
Розв'язання:
Методом добору.
Припустимо, що сестра має одну сестру, тоді братів у неї удвоє більше, тобто два, один з яких є тим хлопчиком, а тому має одного брата і дві сестри, що суперечить умові, що братів і сестер у нього порівно.
Припустимо, що сестра має двох сестер, тоді братів у неї удвоє більше, тобто чотири, один з яких є тим хлопчиком, а тому має трьох братів і трьох сестер, тобто братів і сестер у нього порівно. Разом дітей 3+4=7 дітей.
Відповідь: у сім’ї 7 дітей.